颗粒阻尼技术研究综述

鲁 正，吕西林，闫维明

(1.同济大学 土木工程防灾国家重点实验室，上海 200092;2.北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124)

颗粒阻尼(Particle Damping)技术利用在振动体中有限封闭空间内填充的微小颗粒间摩擦与冲击作用消耗系统振动能量，具有耐久性好、可靠度高、对温度变化不敏感(在颗粒金属熔点以下均可正常使用，钨粉能承受近2 000℃高温)，易用于恶劣环境等优点。颗粒阻尼器为附加质量式被动阻尼器，可增加结构阻尼。该技术在机械和航空航天领域应用较多，但其减振机理未被很好解释。本文对颗粒阻尼技术的起源、发展及研究现状简要评述，重点探讨其在土木工程领域应用的发展趋势。

1 颗粒阻尼技术起源及发展应用

颗粒阻尼为Pagat［1］在研究涡轮机叶片减振问题时发明的冲击减振器(Impact Damper)。该单颗粒冲击阻尼器碰撞时会产生较大噪音与冲击力，对设计参数(如颗粒恢复系数，外界激励强度等)变化敏感。故此后的研究用许多等质量小颗粒代替单一固体质量块，因而产生了颗粒阻尼器。据单元内颗粒数目的不同，传统颗粒阻尼器可分四类，即单单元单颗粒冲击阻尼器 (Impact Damper)［2］、多单元单颗粒冲击阻尼器(Multi-unit Impact Damper)［3］、单单元多颗粒阻尼器(Particle Damper，或称非阻塞性颗粒阻尼器，Non-obstructive Particle Damper)［4-5］及多单元多颗粒阻尼器(Multi-unit Particle Damper)［6］(图 1)。此外，有很多颗粒阻尼器变体，如克服方向依赖性的梁式冲击阻尼器(Beam-like Impact Damper)［7］;用软质包袋将颗粒包裹的“豆包”阻尼器(Bean Bag Impact Damper)［8-9］、用软质材料覆盖容器壁形成缓冲冲击阻尼器(Buffered Impact Damper)［10-11］;带活塞的颗粒阻尼器(Piston-based Particle Damper)［12］;带颗粒减振剂的碰撞阻尼器［13］以及颗粒碰撞阻尼动力吸振器［14-15］等。

颗粒阻尼技术的耗能机理为颗粒间耗能及颗粒与主体结构间冲击耗能［16］。利用颗粒间耗能控制振动体振动已成熟应用，如将装满颗粒的袋子压在振动体上;将颗粒材料绕在振动体周围;在金属切削机床床身用封砂结构，可提高床身阻尼8～11倍［17］等。其减振机理包括:Kerwin［18］提出颗粒材料消耗系统能量的三条途径为颗粒间摩擦、颗粒间接触点处非线性变形及颗粒材料共振;Lenzi［19］认为颗粒间干摩擦是阻尼产生的主要机理;孙进才等［20］认为阻尼来自于沙子损耗掉结构体辐射出的声能。冲击阻尼理论典型代表是以刚性质量块作为冲击体的单冲击减振器，即颗粒阻尼器起源。冲击减振机理包括:屈维德等［21-22］认为冲击减振机理是基于非完全弹性碰撞产生的能量损失;Popplewell［9］认为冲击减振主要通过碰撞过程中动量交换实现;张济生等［23］认为反映冲击减振本质的是冲击体作用于主系统动反力大小及相位等。

图1 各种阻尼器Fig.1 Dampers

尽管颗粒阻尼减振的物理本质尚无定论，但并不影响其在航空航天及机械等领域的成功应用。如雷达天线、印刷线路板减振保护;降低灯柱、烟囱及细高挠性建筑物因风激起的振动;抑制继电器，飞行器及金属切削机床结构的自激振动等。Lieber等［2］用冲击阻尼器控制飞行器振动，考虑每个周期碰撞两次情形，发现当冲击质量和主体结构相位角相差180°时，减振效果最好。Grubin［24］在假定每个周期对称碰撞两次基础上，得到主体结构振动响应，发现其在共振及材料恢复系数较大时能得到更多阻尼。Oledzki［25］用其控制轻质航天器上长管道振动，采用流变计算模型与试验结果吻合良好。Skipor［26］将其用于印刷装置;Moore 等［27］用于低温状态下工作的火箭引擎涡轮系统高速转子;Sato等［28］用于绘图仪支撑系统;Sims等［29］利用颗粒阻尼器改进机械工件的振动稳定性;Gibson等［30-31］将颗粒阻尼器用于空间，发现系统响应衰减率与最小有效振幅是阻尼器设计的重要参数，采用上千个小颗粒阻尼器使系统成为高度非线性，可在较广频率带上提供大阻尼。Friend等［32-33］均将颗粒阻尼器置于结构位移最大处以得到较大系统阻尼，颗粒可通过非弹性碰撞将动能转化为热能耗散掉。通过对铝质悬臂梁在自由端附加颗粒阻尼器实验得到的阻尼数值表明，冲击阻尼具有高度非线性。

国内关于颗粒阻尼技术的研究集中在航空航天、机械等领域。李伟等［8，36］研究豆包阻尼器减振特性并用于板结构;陈前等［37-38］提出基于碰撞理论的颗粒阻尼计算模型，并应用于航空结构及直升机旋翼桨叶;夏兆旺等［39］研究基于悬臂梁的颗粒阻尼实验并应用于平板叶片;毛宽民等［40-41］提出能模拟不同形状微颗粒组合体的椭球状散体元模型;胡溧等［42］研究颗粒阻尼动态特性并用于汽车车身;杜妍辰等［43］研究微颗粒阻尼器的建模方法;赵玲等［44］研究非阻塞性微颗粒阻尼柱的阻尼特性;闫维明等［45］对颗粒阻尼技术做了很有意义介绍;鲁正等［46-50］建立起附加颗粒阻尼器结构的数值计算模型并通过振动台试验得以验证等。

2 颗粒阻尼理论分析与数值模拟

对颗粒阻尼的理论分析主要以单自由度系统为对象。由于冲击阻尼器工作时，冲击块体与主体结构碰撞引起运动量(速度)的突变，使其动力学行为表现出很强的非线性，因而只能求得单颗粒阻尼器结构在简单激励下，在稳态振动时假设每个周期对称碰撞两次情况下的解析解。冲击阻尼器理论分析最早始于Lieber等［2］，其将碰撞视为完全塑性碰撞。Grubin［24］引入碰撞弹性恢复系数，考虑碰撞时的能量损失，建立起单自由度系统附加冲击阻尼器在简谐激励作用下的理论模型。Masri［51］将该假设扩展到每个周期非对称碰撞两次情形。Bapat［52］采用非线性控制方程分析单自由度系统在简谐激励作用下每个周期碰撞N次的振动情况。Masri［3，51，53］推导出单单元单颗粒和多单元单颗粒冲击阻尼器附加在主体结构在周期激励下稳态振动时的解析解，并分析其运动稳定性。Bapa等［54］分析库伦摩擦力影响，绘制了单单元单颗粒冲击阻尼器受迫振动时反映最佳净距和相应的振幅折减幅度表格。Ema等［56］研究表明冲击阻尼器为主体结构提供的附加阻尼由质量块与主体结构碰撞产生，且最佳阻尼作用受质量比和净距共同影响。Duncan等［57］用数值模拟方法研究了竖向冲击阻尼器在宽频和多种振幅下的阻尼特性。

针对考虑颗粒之间相互作用的多颗粒阻尼器结构较难求得解析解问题，已研究出简化方法和数值方法。Papalou 等［4，58-59］将多颗粒阻尼器简化等效为等质量单颗粒阻尼器。Friend等［33］通过将多颗粒模拟为一个凝聚的质量块，将各种机理引起的能量耗散打包为“有效恢复系数”，该系数由实验拟合得到，从而提出一种解析方法。Liu等［60］在归纳实验结果基础上，采用等效粘滞阻尼模拟颗粒阻尼器非线性特质。Xu等［61］提出阻尼作用与各参数关系基于实验拟合的颗粒阻尼器设计经验方法。Wu等［62］将多相流体理论引入颗粒阻尼器分析，提出理论模型。Fang等［63］在文献［62］基础上改进，减少分析的复杂度和计算量。运用于颗粒阻尼模拟方法另如:回归模型法［64］，恢复力曲面法［65］，功率输入法［66］，神经网络法［67］等。尽管上述简化模型及实验研究取得一定成果，但均基于现象，结论较难推广到除该实验之外的其他情形。而离散单元法(Discrete Element Method)［6，41，47，68］的引入使颗粒阻尼器分析研究又进一步，该方法能考虑颗粒之间及颗粒与容器壁之间的相互作用，能更合理定量分析颗粒阻尼器性能。

离散单元法［69］按时步迭代求解，将离散体划分为众多离散单元的集合，据接触定律及牛顿第二定律描述其运动。该方法认为只要时步取值足够小，在该时步内，单元扰动只会传播到与其相邻的单元，不会传播到其他更远单元。据此，作用在某一单元上的外力即可通过与其相邻单元相互作用情况求得，进而求得整个离散体的整体运动形态。

图2(a)为在顶层附加颗粒阻尼器的多自由度结构，其控制方程为:

式中:M，C，K分别为质量、阻尼、刚度矩阵;F，E，分别为接触力向量、地面加速度引起的结构质量矩阵及地面加速度;Xi为i层位移;Mi，Ci，Ki分别为i层质量、阻尼、刚度;Fi为颗粒对i层结构的接触力。

对颗粒i，某一时刻的控制方程为:

式中:mi，Ii为颗粒质量与惯性矩;g为重力加速度向量;Pi，φi为颗粒位置向量与角位移向量;，为颗粒i，j之间的法向接触力及切向接触力(若颗粒i与容器壁接触，则j代表容器壁)，接触力作用在两颗粒接触点非颗粒质心;切向接触力产生扭矩Tij，使颗粒产生旋转;对半径为ri的球形颗粒，Tij=rjnij×，其中，nij为颗粒i质心指向颗粒j质心的单位向量，×表示向量叉积，ki为与颗粒i接触的颗粒数目。

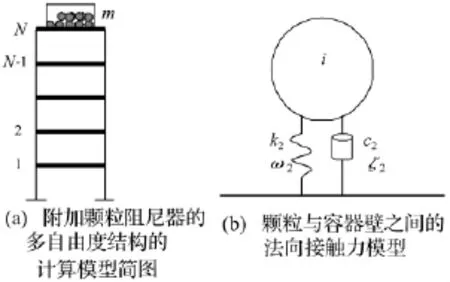
图2 两种模型Fig 2 Model two

Elperin等［70-71］用各种接触力模型定量确定法向力与切向力。采用较多、较简单的有法向为线性接触力模型及切向为库伦摩擦力模型。

图2(b)为颗粒与容器壁法向线性接触力模型，k2为弹簧刚度，为角频率，可通过合理选择ω2((ω2/ωn≥20［72］)模拟刚性壁;c2为阻尼系数，ζ2=c2/2mω2为临界阻尼比，用于模拟非弹性碰撞，故各种恢复系数(Coefficient of Restitution，两物体碰撞后与碰撞前相对速度比值绝对值)可通过调整ζ2实现。颗粒之间的法向线性接触力模型类似，用ω3，c3，ζ3代表颗粒间模拟法向弹簧刚度、阻尼系数、临界阻尼比。法向力表示为:

式中:δn，为颗粒i相对j的位移及速度，ti为颗粒与容器壁距离。

采用库仑摩擦力模型，切向接触力表示为:

式中:μs为颗粒间或颗粒与容器壁间的摩擦系数，为颗粒i相对颗粒j的切向速度。

应用离散单元法模拟附加颗粒阻尼器多自由度体系过程简述为:① 判断颗粒之间，颗粒与容器壁之间相对位置，若δn＞0，作用在颗粒上的接触力可通过式(9)、式(10)求得;若δn≤0，无接触力;② 对作用在一个颗粒上的所有接触力求和，包括颗粒之间接触力和颗粒与容器壁接触力;③ 颗粒的运动可通过式 (8)求得;以上过程对所有颗粒顺次进行;④ 累加所有颗粒与容器壁的接触力，即得式 (1)力F，对F求解，即得主体结构响应。

3 颗粒阻尼试验研究

各种颗粒阻尼器试验目的，一为验证计算结果的正确性，二为研究各种动力荷载下不同阻尼器参数对系统减振效果影响。Veluswami等［73-74］用三种不同材料做阻尼器内部冲击板涂层，发现软质材料恢复系数较小，共振时提供的附加阻尼也小;Sadek等［75-76］考察重力对冲击阻尼器影响，发现阻尼器无重力影响时效果更好，在共振区域附近，每个周期非对称碰撞两次的碰撞形式占主导;Cempel等［77］研究颗粒阻尼器的振动阻尼，发现冲击颗粒能量耗散不仅依赖于内部颗粒碰撞，且与外部碰撞(颗粒与容器壁碰撞)及摩擦相关;Hollkamp等［78］用金属与陶瓷颗粒作冲击体，容器振动时能量通过颗粒碰撞耗散;Saeki等［68］研究简谐激励下颗粒阻尼器响应，发现冲击体质量越大为结构提供的附加阻尼越多，而质量较小冲击体在主体结构振动初始地产生作用更迅速，并定出最佳净距值。Yang等［81-82］总结一系列设计曲线以预测颗粒阻尼器特性。Li等［83］用一系列实验研究单颗粒冲击阻尼器附加在多自由度体系的性状，考察冲击体质量、净距、激励类型及位置等影响，发现增加颗粒质量不一定能增加主体结构各阶模态阻尼。毛宽民等［84］应用三维离散单元法验证试验结果，考察颗粒阻尼器性能，发现该装置提供的较大附加阻尼为冲击阻尼及摩擦阻尼综合作用，导致主体系统振幅在一定时间内呈线性迅速衰减。徐志伟等［85］证实颗粒阻尼器能量耗散机理主要与摩擦及碰撞相关，并重点考察纵向应变梯度引起的剪切摩擦力对阻尼的贡献。实验表明颗粒阻尼器在较宽频带范围内均能提供附加阻尼，用多颗粒作为冲击体，合理考虑冲击、摩擦及剪切机理影响，即能得到最佳附加阻尼。周宏伟等［16］完成了颗粒阻尼应用于飞机蒙皮结构和直升机桨叶的试验。鲁正等［49-50］完成了三层钢框架附加颗粒阻尼器的振动台试验，考察了不同地震波输入下的系统减震效果。

4 颗粒阻尼技术在土木工程中应用

土木结构存在各种振动，使结构振动控制体系应运而生。Yao［86］最早将现代控制理论应用于土木结构。Kelly等［87-88］提出用外加耗能装置耗散结构振动能量设想。由此，消能减震技术逐渐得以应用，并研制、开发简单实用高效的新型消能减震装置。应用较广的被动控制装置有粘弹性阻尼器、摩擦阻尼器、流体阻尼器及调谐质量阻尼器等。然而，粘弹性材料在高温与低温环境下会失效、退化变脆分解;摩擦阻尼器虽能用于某些高温情形(如涡轮片)，但其性能与两物体切合的紧密程度等因素有关，有效性会因物体表面状况改变而降低，且在各种动力作用下会发生材性退化与疲劳效应;流体阻尼器因渗漏较难用于恶劣环境(极端温度);调谐质量阻尼器(Tuned Mass Damper，TMD)只能在共振区附近较小频率范围内有效，且对工作环境变化敏感。因此，广泛应用于机械领域的高度非线性颗粒阻尼技术体现出在土木工程应用的良好前景和发展潜力。

颗粒阻尼技术应用于土木工程的研究刚起步，实际工程应用较少见。Ogawa等［89］将冲击阻尼器用于悬索桥桥塔以控制风振;Naeim等［90］介绍位于圣地亚哥市中心经受2010年智利地震考验的附加颗粒阻尼器的高层建筑(图3);Liu等［91］将颗粒阻尼用于层状蜂窝夹层结构抗冲击碰撞问题研究，但其试验对象仍为悬臂结构;赵玲等［44］对微颗粒阻尼薄壁柱(边长25 mm、壁厚0.6 mm正方形薄壁空心柱)的阻尼特性进行了初步试验研究;张向东［92］初步探讨了颗粒阻尼器的颗粒材料、布置位置和质量比等对建筑结构减振控制效果影响;杨智春［14］对颗粒碰撞阻尼动力吸振器用于5层楼房框架模型的抑振情况进行了试验研究;鲁正［93］对不同地震激励下带颗粒阻尼器的框架结构进行了理论、试验研究及参数分析。

图3 Parque Araucano楼及阻尼器系统Fig.3 The Parque Araucano building and its particle damper system

颗粒阻尼减振频带宽，在0～6 000 Hz范围内均有一定减振效果［5，94］，因此可考虑用其抑制土木结构地震、风振等低频振动及地铁、高架交通引起的环境振动等，且减振性能不随时间而降低，能有效抑制共振峰值;据颗粒材料特性，该技术尤其适用野外极端条件结构，如输电塔振动控制等。此外，主体结构因附加颗粒质量，故可降低共振频率;颗粒布置灵活，可同TMD附加于土木结构外部，也可内嵌于构件中，且在任意夹层、内部空洞均可放置，原结构改动小，不影响结构使用;所用颗粒取材廉价方便，如钢球、沙子、石子等均可使用。因此，该技术在土木工程中适用性大大增强［45］。

然而，目前颗粒阻尼理论计算模型较单一，无法针对不同工作状态下不同颗粒阻尼进行较准确的内部接触力与耗能情况的定量分析;已有文献对附加颗粒阻尼器主体结构的研究多集中在单自由度系统或机械中常用悬臂梁结构，对多自由度结构附加颗粒阻尼器的精细分析尚未开展;由于诸多因素对颗粒阻尼器的减振效果有影响，尝试寻找最佳参数或能综合诸多因素影响的新参数，优化颗粒阻尼器工作性能;为增强颗粒阻尼器减振效果而对传统颗粒阻尼技术进行的改进目前尚少;对土木结构使用颗粒阻尼器后在地震及风振下的控制效果理论及试验研究更少;对颗粒阻尼设计标准化、规范化，能指导工程应用的实用设计方法研究基本未见。

5 结论

由以上讨论知，虽对颗粒阻尼进行诸多理论，数值及试验研究，但主要仍为基础性研究;利用数值模拟方法将简化的基于经验与试验的模拟转向较精细的基于三维离散元法的模拟同样存在缺点，如对具体材料属性参数取值要求高且计算量随颗粒数目的增加而急剧增大等。因此，颗粒阻尼用于土木工程前景与发展潜力良好，对掌握颗粒阻尼本质，进行规范化设计与实例应用尚需深入研究、实践。

［1］Paget A L.Vibration in steam turbine buckets and damping by impacts［J］.Engineering，1937，143:305-307.

［2］Lieber P， Jensen D P. An acceleration damper:development， design and some applications ［J］.Transactions of the ASME，1945，67(7):523-530.

［3］Masri S F.Analytical and experimental studies of multipleunit impact dampers［J］.Journal of the Acoustical Society of America，1969，45(5):1111-1117.

［4］Papalou A，Masri S F.Performance of particle dampers under random excitation［J］.Journal of Vibration and Acoustics-Transactions of the Asme，1996，118(4):614-621.

［5］Panossian H V.Structural damping enhancement via nonobstructive particle damping technique［J］.Journal of Vibration and Acoustics，1992，114(1):101-105.

［6］Saeki M.Analytical study of multi-particle damping［J］.Journal of Sound and Vibration，2005，281(3-5):1133-1144.

［7］Chen L A，Semercigil S E.A beam like damper for attenuating transient vibrations of light strucvtures ［J］.Journal of Sound and Vibration，1993，164(1):53-65.

［8］李 伟，朱德懋，胡选利，等.豆包阻尼器的减震特性研究［J］.航空学报，1999，20(2):168-170.

LI Wei，ZHU De-mao，HU Xuan-li，et al.Study on the damping characteristics of bean bag damper［J］.Journal of Aeronautics，1999，20(2):168-170.

［9］Popplewell N，Semercigil S E.Performance of the bean bag impact damper for a sinusoidal external force［J］.Journal of Sound and Vibration，1989，133(2):193-223.

［10］Li K，Darby A.A buffered impact damper for multi-degreeof-freedom structural control［J］.Earthquake Engineering ＆Structural Dynamics，2008，37(13):1491-1510.

［11］段 勇，陈 前.软内壁颗粒阻尼器阻尼特性试验研究［J］.振动工程学报，2011，24(2):215-220.

DUAN Yong，CHEN Qian.Experimental investigation of damping properties of the particle dampers with soft lining［J］.Journal of Vibration Engineering，2011，24(2):215-220.

［12］ Shah B M，Pillet D，Bai X M，et al.Construction and characterization of a particle-based thrust damping system［J］.Journal of Sound and Vibration，2009，326(3-5):489-502.

［13］杜妍辰，王树林，朱 岩，等.带颗粒减振剂碰撞阻尼的减振特性［J］.机械工程学报，2008，44(7):186-189.

DU Yan-chen，WANG Shu-lin，ZHU Yan，et al.Vibration characteristics of a new fine particle impact damping［J］.Chinese Journal of Mechanical Engineering，2008，44(7):186-189.

［14］杨智春，李泽江.颗粒碰撞阻尼动力吸振器的设计及实验研究［J］.振动与冲击，2010，29(6):69-71.

YANG Zhi-chun，LI Ze-jiang.Design and test for a type of particle impact damped dynamic absorber［J］.Journal of Vibration and Shock，2010，29(6):69-71.

［15］ Semercigil S E，Collette F，Huynh D.Experiments with tuned absorber-impact damper combination［J］.Journal of Sound and Vibration，2002，256(1):179-188.

［16］周宏伟.颗粒阻尼及其控制的研究与应用［D］.南京:南京航空航天大学，2008.

［17］戴德沛.阻尼减振降噪技术［M］.西安:西安交通大学出版社，1986.

［18］ Kerwin E M.Macro-mechanisms of damping in composite structures［A］.Internal Friction Damping and Cyclic Plasticity［C］.Baltimore，Md:ASTM-STP，1965:125-147.

［19］ Lenzi A.The use of damping material in industrial machine［D］.England:University of Southampton，Institute of Sound and Vibration Research，1985.

［20］ Sun J C，Sun H B.Predictions of total loss factors of structures Part II:loss factors of sand filled structure［J］.Journal of Sound and Vibration，1986，104(2):243-257.

［21］屈维德.机械加工中的振动问题［M］.北京:高等教育出版社，1959.

［22］邓危梧.冲击减振器的效应及其基本参数的确定［J］.机械工程学报，1964，12(4):83-94.

DENG Wei-wu.Effects of impact damper and determination of itsparameters［J］. ChineseJournalofMechanical Engineering，1964，12(4):83-94.

［23］张济生，何康渝.关于冲击减振机理的讨论［A］.中国机械工程学会机械动力学会第四届学术年会论文集［C］.天津:天津大学出版社，1990:316-321.

［24］ Grubin C.On the theory of the acceleration damper［J］.Journal of Applied Mechanics，1956，23(8):373-378.

［25］ Oledzki A.New kind of impact damper-from simulation to real design ［J］.Mechanism ＆ Machine Theory，1981，16(3):247-253.

［26］ Skipor E，Bain L J.Application of impact damping to rotary printing equipment［J］.Journal of Mechanical Design，1980，102(2):338-343.

［27］ Moore J J，Palazzolo A B，Gadangi R，et al.Forced response analysis and application of impact dampers to rotor-dynamic vibration suppression in a cryogenic environment［J］.Journal of Vibration and Acoustics，1995，117(3A):300-310.

［28］ Sato T，Takase M，Kaiho N，et al.Vibration reduction of pantograph-support system using an impact damper(influence of curve track)［A］.Proceeding of International Conference on Noise ＆ Vibration Engineering，ISMA ［C］.Leuven，Belgium:2002:1669-1676.

［29］Sims N D，Amarasinghe A，Ridgway K.Particle dampers for workpiece chatter mitigation［J］.Manufacturing Engineering Division，ASME，2005，16(1):825-832.

［30］ Gibson B W.Usefulness of impact dampers for space applications［R］.AFIT/GA/AA/83M-2，147.Wright-Patterson AFB，OH:Air Force Institute of Technoligy，1983.

［31］ Torvik P J，Gibson W.Design and effectiveness of impact dampers for space applications［J］.Design Engineering Division，ASME，1987，5:65-74.

［32］ Friend R D，Kinra V K.Measurement and analysis of particle impact damping［A］.Proceedings of SPIE Conference.Passive Damping and Isolation［C］.San Jose，CA:SPIE，1999:20-31.

［33］ Friend R D，Kinra V K.Particle impacting damping［J］.Journal of Sound and Vibration，2000，233(1):93-118.

［34］ Marhadi K S，Kinra V K.Particle impact damping:effect of mass ratio，material and shape［J］.Journal of Sound and Vibration，2005，283(1):433-448.

［35］ Olson S E.An analytical particle damping model［J］.Journal of Sound and Vibration，2003，264(5):1155-1166.

［36］李 伟，朱德懋，黄协清.柔性约束颗粒阻尼于板结构的减振研究［J］.噪声与振动控制，1998，4(1):2-5.

LIWei， ZHU De-mao， HUANG Xie-qing， Vibration reduction effect of bean bag particle damping on plan structure［J］.Noise and Vibration Control，1998，4(1):2-5.

［37］王青梅，陈 前.基于碰撞理论的颗粒阻尼计算模型及试验研究［J］.振动、测试与诊断，2007，27(4):300-303.

WANG Qing-mei，CHEN Qian.Computational model based on collision theory and experimental study on particle damping［J］.Journal of Vibration，Measurement＆ Diagnosis，2007，27(4):300-303.

［38］段 勇，陈 前，林 莎.颗粒阻尼对直升机旋翼桨叶减振效果的试验［J］.航空学报，2009，30(11):2113-2118.

DUAN Yong， CHEN Qian， LIN Sha. Experimentsof vibration reduction effect of particle damping on helicopter rotor blade［J］.Journal of Aeronautics，2009，30(11):2113-2118.

［39］夏兆旺，单颖春，刘献栋，等.颗粒阻尼应用于平板叶片减振试验［J］.振动、测试与诊断，2008，28(3):269-272.

XIA Zhao-wang，SHAN Ying-chun，LIU Xian-dong，et al.Particle damping tests on cast steel plates［J］.Journal of Vibration，Measurement ＆ Diagnosis， 2008，28(3):269-272.

［40］毛宽民，师汉民，黄其柏，等.NOPD的椭球状散体元建模［J］.工程力学，2000，17(6):65-71.

MAO Kuan-min，SHI Han-min， HUANG Qi-bai，et al.Three dimensional ellipsoidal element DEM model of NOPD［J］.Engineering Mechanics，2000，17(6):65-71.

［41］Mao K M，Wang M Y，Xu Z W，et al.DEM simulation of particle damping［J］.Powder Technology，2004，142(2-3):154-165.

［42］ Hu L，Huang Q B，Liu Z X.A non-obstructive particle damping model of DEM ［J］.International Journal of Mechanics and Materials in Design，2008，4(1):45-51.

［43］ Du Y C， WangS L. Energydissipation in normal elastoplastic impact between two spheres［J］.Journal of Applied Mechanics，2009，76(6):061010-061017.

［44］赵 玲，刘 平，卢媛媛.非阻塞性微颗粒阻尼柱阻尼特性的实验研究［J］.振动与冲击，2009，28(8):1-5.

ZHAO Ling， LIU Ping， LU Yuan-yuan. Experimental investigation on damping characteristics of NOPD columns［J］.Journal of Vibration and Shock，2009，28(8):1-5.

［45］闫维明，黄韵文，何浩祥，等.颗粒阻尼技术及其在土木工程中的应用展望［J］.世界地震工程，2010，26(4):18-24.

YAN Wei-ming，HUANG Yun-wen，HE Hao-xiang，et al.Particle damping technology and its application prospect in civil engineering［J］.World Earthquake Engineering，2010，26(4):18-24.

［46］ Lu Z，Lu X L，Masri S F.Studies of the performance of particle dampers under dynamic loads［J］.Journal of Sound and Vibration，2010，329(26):5415-5433.

［47］ Lu Z，Masri S F，Lu X L.Parametric studies of the performance of particle dampers under harmonic excitation［J］. SturcturalControland Health Monitoring， 2011，18(1):79-98.

［48］ Lu Z，Masri S F，Lu X L.Studies of the performance of particle dampers attached to a two-degree-of-freedom system under random excitation ［J］.Journal of Vibration and Control，2011，17(10):1454-1471.

［49］ Lu Z，Lu X L，Lu W S，et al.Experimental studies of the effects of buffered particle dampers attached to a multidegree-of-freedom system under dynamic loads［J］.Journal of Sound and Vibration，2012，331(9):2007-2022.

［50］Lu Z，Lu X L，Lu W S，et al.Shaking table test of the effects of multi-unit particle dampers attached to an MDOF system under earthquake excitation［J］.Earthquake Engineering ＆Structural Dynamics，2012，41(5):987-1000.

［51］ Masri S F.General motion of impact dampers［J］.The Journal of the Acoustical Society of America，1970，47(1B):229-237.

［52］ Bapat C N.Periodic motion of an impact oscillator［J］.Journal of Sound and Vibration，1998，209(1):43-60.

［53］ Masri S F.Effectiveness of two-particle impact dampers［J］.Journal of the Acoustical Society of America，1967，41(6):1553-1554.

［54］ Bapat C N，Sankar S.Multiunit impact damper-reexamined［J］.Journal of Sound and Vibration，1985，103(4):457-469.

［55］ Bapat C N，Sankar S.Single unit impact damper in free and forced vibration［J］.Journal of Sound and Vibration，1985，99(1):85-94.

［56］ Ema S，Marui E.Fundamental study on impact dampers［J］. International Journal of Machine Tools and Manufacture，1994，34(3):407-421.

［57］Duncan M R，Wassgren C R，Krousgrill C M.The damping performance of a signle particle impact damper［J］.Journal of Sound and Vibration，2005，286(1-2):123-144.

［58］ Papalou A，Masri S F.Response of impact dampers with granular materials under random excitation［J］.Earthquake Engineering ＆ StructuralDynamics，1996，25(3):253-267.

［59］ Papalou A，Masri S F.An experimental investigation of particle dampers under harmonic excitation［J］.Journal of Vibration and Control，1998，4(4):361-379.

［60］ Liu W，Tomlinson G R，Rongong J A.The dynamic characterisation of disk geometry particle dampers［J］.Journal of Sound and Vibration，2005，280(3-5):849-861.

［61］Xu Z W，Chan K W，Liao W H.An empirical method for particle damping design ［J］.Shock and Vibration，2004，11(5-6):647-664.

［62］ Wu C J，Liao W H，Wang M Y.Modeling of granular particle damping using multiphase flow theory of gas-particle［J］.Journal of Vibration and Acoustics，2004，126(2):196-201.

［63］ Fang X，Tang J.Granular damping in forced vibration:qualitative and quantitative analyses［J］.Journal of Vibration and Acoustics，2006，128(4):489-500.

［64］胡 溧，黄其柏，许智生.颗粒阻尼的回归分析研究［J］.中国机械工程，2008，19(23):2834-2837.

HU Li，HUANG Qi-bai，XU Zhi-sheng.Regression analysis of particle damping［J］.Chinese Mechanical Engineering，2008，19(23):2834-2837.

［65］蒋 华，陈 前.恢复力曲面法在颗粒阻尼器研究中的应用［J］.振动、测试与诊断，2007，27(3):228-231.

JIANG Hua，CHEN Qian.Application of resoting force superface method to particle damping research［J］.Journal of Vibration，Measurement＆ Diagnosis，2007，27(3):228-231.

［66］刘雁梅，黄协清，陈天宁.非阻塞性颗粒阻尼加筋板振动功率流的研究［J］.西安交通大学学报，2001，35(1):61-65.

LIU Yan-mei，HUANG Xie-qing，CHEN Tian-ning.Study on power flow of a stiffened plate with non-obstructive particle damping［J］.Journal of Xi'an Jiaotong University，2001，35(1):61-65.

［67］Tanrikulu A H.Application of ANN techniques for estimating modal damping of impact-damped flexible beams ［J］.Advancesin EngineeringSoftware， 2009， 40(10):986-990.

［68］ Saeki M.Impact damping with granular materials in a horizontally vibrating system ［J］.Journal of Sound and Vibration，2002，251(1):153-161.

［69］Cundall A P A，Strack O D L.A distinct numerical model for granular assemblies ［J］.Geotechnique，1979，29(1):47-65.

［70］ Elperin T，Golshtein E.Comparison of different models for tangential forces using the particle dynamics method ［J］.Physica A:Statistical and Theoretical Physics，1997，242(3-4):332-340.

［71］Renzo A D，Maio F P D.Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes［J］.Chemical Engineering Science，2004，59(3):525-541.

［72］ Masri S F.Steady-state response of a multidegree system with an impact damper［J］.Journal of Applied Mechanics-Transactions of the Asme，1973，40(1):127-132.

［73］Veluswami M A，Crossley F R E.Multiple impacts of a ball between two plates，part 1:some experimental observations［J］.Journal of Engineering for Industry，ASME，1975，97(3):820-827.

［74］ Veluswami M A，Crossley F R E，Horvay G.Multiple impacts of a ball between two plates，part 2:mathematical modeling［J］.Journal of Engineering for Industry，ASME，1975，97(3):835-838.

［75］ Sadek M M，Mills B.Effect of gravity on the performance of an impact damper，part 1:steady-state motion ［J］.Journal of Mechanical Engineering Science，1970，12(4):268-277.

［76］Sadek M M，Williams C J H，Mills B.Effect of gravity on the performance of an impact damper，part 2:stability of vibrational modes［J］.Journal of Mechanical Engineering Science，1970，12(4):278-287.

［77］Cempel C，Lotz G.Efficiency of vibrational energy dissipation by moving shot ［J］.Journal of Structural Engineering，1993，119(9):2642-2652.

［78］ Hollkamp J J，Gordon R W.Experiments with particle damping［A］.Smart Structures and Materials 1998:Passive Damping and Isolation［C］.San Diego:SPIE，1998:2-12.

［79］ Yokomichi I，Araki Y，Jinnouchi Y，et al.Impact damper with granular materials for multibody system［J］.Journal of Pressure Vessel Technology，1996，118(1):95-103.

［80］ Yokomichi I，Muramatsu H，Araki Y.On shot impact dampers applied to self-excited vibrations［J］.International Journal of Acoustics and Vibration，2001，6(4):193-199.

［81］ Yang M Y.Development of master design curves for particle impactdampers［D］. PA:The Pennsylvania State University，Department of Mechanical Engineering，2003.

［82］ Yang M Y，Lesieutre G A，Hambric S A，et al.Development of a design curve for particle impact dampers［J］.Noise Control Engineering Journal，2005，53(1):5-13.

［83］ Li K，Darby A P.Experiments on the effect of an impact damper on a multiple-degree-of-freedom system［J］.Journal of Vibration and Control，2006，12(5):445-464.

［84］ Mao K M，Wang M Y，Xu Z W，et al.Simulation and characterization of particle damping in transient vibrations［J］.Journal of Vibration and Acoustics，ASME，2004，126(2):202-211.

［85］Xu Z W，Wang M Y，Chen T N.Particle damping for passive vibration suppression:numerical modelling and experimental investigation［J］.Journal of Sound and Vibration，2005，279(3-5):1097-1120.

［86］ Yao J T P.Concept of structural control［J］.Journal of the Structural Division，ASCE，1972，98(7):1567-1574.

［87］ Kelly J M，Skinner R L，Heine A J.Mechanics of energy absorption in special devices for use in earthquake-resistant structures［J］.Bulletin of New Zealand National Society for Earthquake Engineering，1972，5(3):63-88.

［88］ Skinner R I，Kelly J M，Heine A J.Hysteretic dampers for earthquake-resistant structures［J］.Earthquake Engineering＆ Structural Dynamics，1974，3(3):287-296.

［89］ Ogawa K，Ide T，Saitou T.Application of impact mass damper to a cable-stayed bridge pylon［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，72(1-3):301-312.

［90］Naeim F，Lew M，Carpenter L D，et al.Performance of tall buildings in santiago，chile during the 27 february 2010 offshore maule，chile earthquake［J］.The Structural Design of Tall and Special Buildings，2011，20(1):1-16.

［91］ Liu A Q，Wang B，Choo Y S，et al.The effective design of bean bag as a vibroimpact damper［J］.Shock and Vibration，2000，7(8):343-354.

［92］张向东.高架路交通诱发振动与建筑物减振控制方法研究［D］.北京:北京工业大学，2009.

［93］鲁 正.颗粒阻尼器的仿真模拟和性能分析［D］.上海:同济大学，2011.

［94］ Panossian H V，Bice D L.Low frequency applications of nonobstructive particle damping［A］.61St shock and vibration symposium［C］.Pasadena，CA:1990.