剪式可展机构非线性动力学分析子系统方法

刘树青，王兴松

(1.东南大学 机械工程学院，南京 211189;2.南京工程学院 先进制造技术工程中心，南京 211167)

剪式机构作为可展机构应用广泛，其基本组成单元为由两个连杆与转动销轴连接的“X”型结构，称为剪式单元。由多个剪式单元相互串接可构成平面多级剪式伸缩机构，将其合理搭接，可形成丰富实用的立体剪式单元。在建筑、工程机械、机器人、空间结构等领域广泛应用。随着航天技术的发展，可展机构成为航天领域研究热点，而剪式机构作为应用最广的可展机构形式，对其拓扑结构、可展开性、运动学、结构动力学等方面的相关研究较受重视［1-4］，而对其机构动力学研究相对较少。

对剪式可展机构，若直接建立动力学模型则会导致方程规模大，求解困难，较难实时仿真与控制。剪式可展机构由剪式单元组合而成，模块化程度高，甚至各剪式单元结构相同或相似。因此，将该机构划分为简单子系统建立运动方程，并利用子系统间的拓扑结构，建立整体系统非线性动力学模型，实现程式化建模，可有效缩减求解规模，对此，文献［5-8］均有研究。

本文针对由相互耦合子系统构成的复杂多体系统剪式可展机构提出高效计算子系统方法。该方法将复杂多体系统划分为简单子系统，分别建立各子系统运动方程，并通过子系统间的递推关系建立整系统运动方程，将求解整体系统大规模运动方程转化为求解子系统小规模运动方程，与传统方法相比，计算效率更高。

1 状态空间子系统运动方程

将剪式单元视为子系统，则多数剪式可展机构在拓扑结构上包含相同子系统，如图1所示。因此，子系统模型便可多次重复使用。剪式可展机构中子系统个数发生变化或设计过程中需更改子系统结构时，均可对动力学模型进行修改，建模过程易于程式化。

图1 剪式机构Fig.1 Scissor-like mechanism

1.1 坐标系及各参数递推表示

多体系统中相邻两连接体及相关坐标系如图2所示，其中i为j的内接体。O-XYZ为惯性坐标系，O'i-X'iY'iZ'i为连接体i体坐标系，位于连接体i的内接关节处，其原点在惯性系中的位置向量为ri，相对惯性系方向矩阵为Ai;O″ij-X″iY″iZ″i位于连接体i的外接关节处，其相对于体坐标系O'i-X'iY'iZ'i的方向矩阵为Cij，O'i与O″ij之间的位置向量为sij;同理可定义连接体j的相关坐标系，O″ij与O'i之间的位置向量为dij。

坐标系建立后，连接体j的位置、速度、加速度均可用其内接体i的相关参数递推表示［5］:

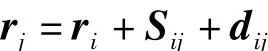
图2 相邻两连接体坐标系Fig.2 Coordinate system of adjacent body

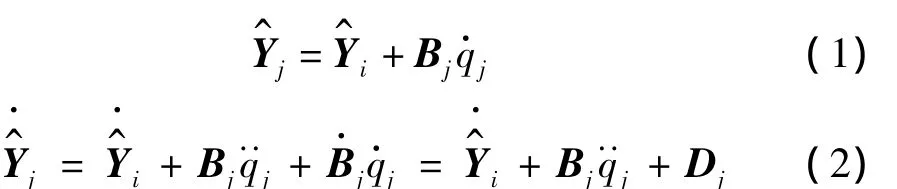
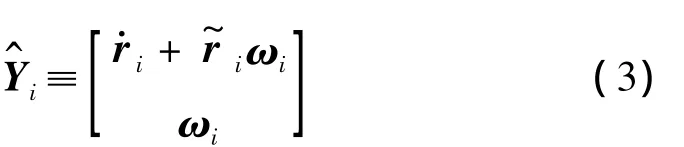
为连接体i的加速度状态向量;为连接体j和i之间的速度转移矩阵;qj为关节j的关节相对坐标，ωi为关节i的角速度向量，Hj为关节j的轴线方向向量。

1.2 子系统运动方程

将式(3)中状态速度用虚位移代替，得虚位移状态变分:

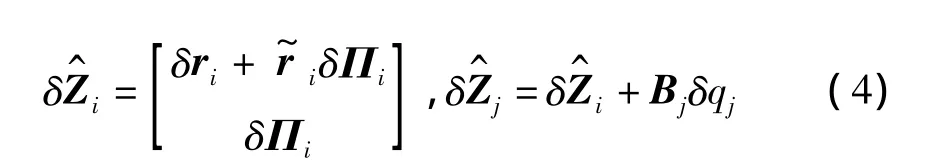
多刚体系统变分形式的牛顿-欧拉方程为［9］:

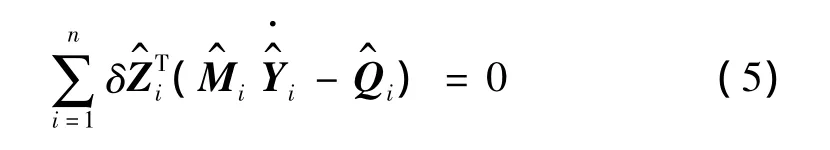
对开环子系统，根据子系统拓扑结构，将式(2)、式(4)的递推关系依次代入式(5)，可得开环子系统运动方程为:

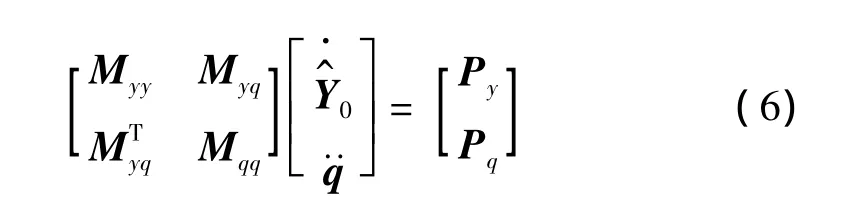
若已知子系统基体加速度，则有:

对闭环子系统，切断连接体n和n'之间的关节，使之成为两个开链，并引入切断关节处的约束力及约束方程，得系统运动方程为:

其中:λ为拉氏乘子，Φq为约束雅各比矩阵。

若已知子系统基体加速度，据式(9)可计算出拉氏乘子及各连接体加速度为:

2 子系统方法

据系统拓扑结构，综合子系统运动方程及约束方程，可建立整个多体系统运动方程，该方程数目多，求解规模大，且在产品设计阶段，如果系统中增加或减少一个子系统，或系统结构发生变化，则需对系统模型做复杂的修正。因此，需一种算法，能使各子系统独立建模计算，且能方便、高效评价对整体系统影响。

2.1 子系统等效

为每个独立子系统增加一个虚物体，子系统通过该虚物体与基体或其他子系统相连，如图3所示。

图3 子系统及虚物体Fig.3 subsystem and virtual body

虚物体无惯量、重力等动力学性质，只用于建立参考系便于描述子系统相对运动。若虚物体运动已知，则其对应的子系统的动力学分析可独立进行。在整体系统动力学分析中，须计算每个子系统的动力学影响。

将式(7)代入式(6)得开环子系统对其基体的等效质量矩阵及等效力向量分别为:

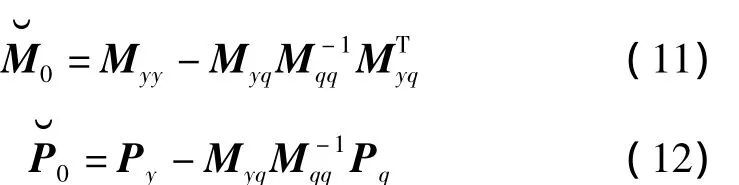
将式(9)、(10)代入式(8)得闭环子系统对基体的等效质量矩阵及等效力向量为:

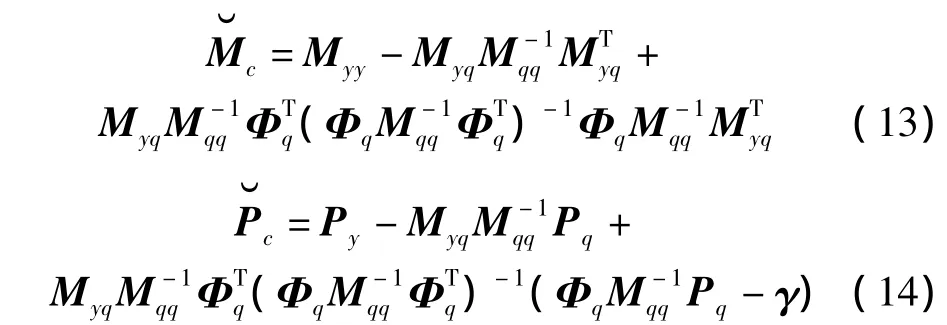
2.2 整体系统运动方程

对图4由相互耦合的开环或闭环子系统构成的复杂多体系统，可将其划分为图5所示几个子系统。每个子系统通过虚物体与内接子系统相连。

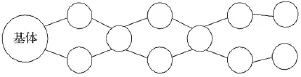
图4 子系统间相互耦合的多体系统Fig.4 Multibody system with intercoupled subsystems

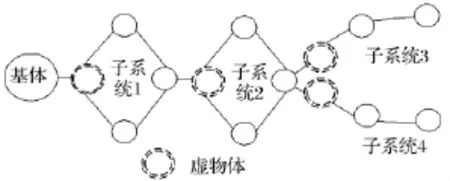
图5 子系统划分及等效Fig.5 Subsystem division and the effective model

由求解闭环约束方程得到的子系统位置与速度，可求得子系统内所有物体与关节的位置及速度。子系统虚物体与其内接子系统的连接体运动相同，因此，位置与速度分析可沿正向从第一个子系统向末端子系统递推。

完成位置和速度分析后，运用式(11)、(12)或式(13)、(14)从末端子系统向内部子系统反向递推，计算每个子系统的等效质量矩阵及等效力向量。在此过程中，外部子系统的等效质量矩阵及等效力向量与相邻内部子系统的连接体质量矩阵及力向量相加。最终得到整条路径等效到基体的质量矩阵及力向量。系统运动方程可表示为:

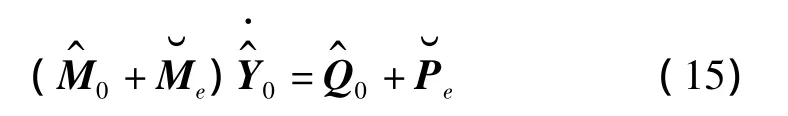
式(15)中，无论子系统自由度多大、有几个子系统相互串接，矩阵维数始终为6×6，向量维数为6×1，大大降低了整体系统的求解规模，提高了计算效率，而编程中也便于增加或删除某个子系统对整体系统的影响，若子系统内部结构发生变化，修改程序也只限于相应的子系统内部。

与传统微分代数方程动力学模型计算效率比较见图6，图中，横坐标为多体系统自由度数(DOF)，纵坐标为两种方法的建模及求解时间，该时间Intel i5 2450 M CPU，2.5 GHz，4 GB RAM 计算机的 Mathematica 软件所得。当系统自由度数小于25时，子系统递推方法的计算效率低于传统微分代数模型;随着系统自由度数目的增加，子系统递推方法的计算效率明显提高，自由度数越多，效率越明显。

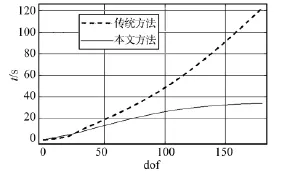
图6 计算效率对比Fig.6 Comparison of computational efficiency

3 剪式可展机构非线性动力学计算

运用上述子系统方法对图7三级平面剪式机构进行多体动力学建模，并在Mathematica环境下编程仿真。

本文剪式机构主要参数为:杆件矩形截面宽b=5 mm，高h=30 mm，干架长度l=1 000 mm，材料密度ρ=2 750 kg/m3，弹性模量E=70 ×109N/m2，初始角度θ1=30°。

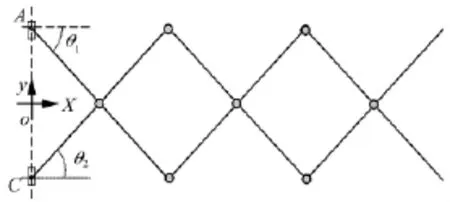
图7 三级剪式机构简图Fig.7 Diagram of 3-level scissor-like mechanism

外力为施加于A、C两点的驱动力:

三级剪式机构由三个相同剪式单元串联，传统建模方法建立的动力学模型为36×36维，本文将每个剪式单元作为一个子系统建立动力学模型，得到其等效质量矩阵及等效力向量，从末端依次向根部递推，则可得整个系统6×6维的等效质量矩阵及等效力向量，从而降低求解规模。各节点位置、速度、加速度可通过从根部向末端的正向递推求得。

为验证子系统方法的正确性，建立三级剪式机构拉格朗日动力学模型，仿真结果为图8中虚线，子系统方法仿真结果为图8中实线。图8(a)、(b)、(c)分别为图7中角度θ1的角位置、角速度及角加速度随时间的变化关系曲线，子系统模型仿真结果与拉格朗日模型仿真结果基本一致，由此验证了子系统方法的正确性。由于拉格朗日模型采用解析方法，而子系统模型采用数值方法，存在一定计算误差，故图中曲线不完全重合。

图8 仿真结果Fig.8 Simulation results

4 结论

将剪式可展机构划分成简单子系统，为每个子系统添加虚物体，独立求解每个子系统的运动方程，并根据子系统间的拓扑关系进行组合或递推，得到整个系统的等效质量矩阵及等效力向量，从而减小了求解规模。该建模方法适用于具有多个相互耦合的开环或闭环子系统的复杂多体系统，建模方法易于程式化。通过与传统方法比较验证了该方法的正确性。

［1］杨 毅，丁希仑.剪式单元可展机构静力学分析与拓扑优化设计［J］.中国机械工程，2010，21(2):184-189.

YANG Yi，DING Xi-lun.Analysis and topology optimization of deployable mechanism based on pantograph［J］.China Mechanical Engineering，2010，21(2):184-189.

［2］ Kipe G，Söylemez E， Özgür Kisisel A U.A family of deployable polygons and polyhedral［J］.Mechanism and Machine Theory，2008，43(5):627-640.

［3］ Cherniavsky A G，Gulyayev V I，Gaidaichuk V V，et al.Large deployable space antennasbased on usage ofpolygonal pantograph［J］.Journal of Aero Space Engineering，2005，18(3):139-145.

［4］ Oh J K，Lee A Y.Design and control of bridge inspection robot system［C］.Proceedings of the IEEE International Conference on Mechatronics and Automation，2007:3634-3639.

［5］ Kim S S.A subsystem synthesis method for efficient vehicle multibody dynamics［J］.Multibody System Dynamics，2002，7(2):189-207.

［6］王 皓，林忠钦，来新民.平面机械系统动力学建模的复合方法［J］.中国科学 E 辑:技术科学，2008，38(5):715-728.

WANG Hao，LIN Zhong-qin，LAI Xin-min.Composite method for dynamics modeling of planar mechanical system［J］.Science in China，2008，38(5):715-728.

［7］ Jain A.Recursive algorithms using local constraint embedding for multibody system dynamics［C］.Proceedings of the ASME 2009 International Design Engineering Technical Conferences＆Computers and Information in Engineering Conference.San Diego，USA:ASME，2009，4:139-147.

［8］ Kim S S，Wang J H.Subsystem synthesis methods with independent coordinates for real-time multibody dynamics［J］.Journal of Mechanical Science and Technology，2007，19(1):312-319.

［9］ Tsai F F，Haug E J.Real-time multibody system dynamic simulation:partⅠ a modified recursive formulation and topologicalanalysis ［J］. Mechanics Based Design of Structures and Machines，1991，19(1):99-127.