基于独立分量分析的欠定盲源分离方法

杨 杰，俞文文，田 昊，关珍贞

(1.军械工程学院，石家庄 050003;2.华阴兵器试验中心，陕西 华阴 714200)

齿轮箱发生故障时常出现多种故障并发情形，用诊断单一故障的频谱诊断法、轴心轨迹法、小波诊断法已不再有效，而盲源分离技术为较有效的机械复合故障诊断方法。但已有研究基本针对超定盲分离而言，即要求观测器个数多于或等于源信号个数。少于源信号个数的欠定盲分离问题，已成为盲信号处理领域中挑战性问题。

源数多于传感器数时，机械故障源分离主要考虑稀疏源，利用源信号稀疏性估计混合矩阵;源稀疏性较好时，通过聚类方法可达到较好的盲分离效果［1-2］。源信号稀疏性较差时，虽可利用稀疏性得到混合矩阵估计，但通过聚类方法得不到较好的分离效果。

独立分量分析(ICA)是解决盲源分离问题(BSS)的主要算法，其可使输出信号各分量统计独立以实现信号分离。已有多种不同算法［3-5］，如扩展Infomax算法。由于其既能分离超高斯信号，也能分离亚高斯信号，因而得到广泛应用。但该算法只能用于超定盲分离。本文提出的欠定ICA算法，通过生成隐藏数据将欠定盲分离转化为超定盲分离问题，再用扩展Infomax算法对信号进行分析。该方法可分离欠定情形下超高斯与亚高斯混合信号。结合包络阶次方法对齿轮箱实测瞬态信号进行分析，找到故障特征，验证该方法的有效性。

1 基于独立分量分析的盲源分离算法

1.1 独立分量分析问题描述

图1为x(t)由m个传感器获得m路观测信号，每个观测信号由n个独立源信号si(t)(i=1，2，…，n)的线性混合，即:

式中:x(t)=［x1(t)，x2(t)，…，xm(t)］T为m个混合信号，s(t)=［s1(t)，s2(t)，…，sn(t)］T为n个未知源信号，A=［a1，a2，…，an］为未知的m×n维混叠矩阵，ICA算法目的为从多路观测信号x中分离出隐含其中的源信号s，即寻找分离矩阵W，有:

式中:u(t)=［u1(t)，u2(t)，…，um(t)］T为对隐含源信号分量s的逼近。

图1 盲源分离原理图Fig.1 The principle sketch of blind source separation

1.2 扩展的Infomax算法

Infomax算法［4］处理过程为:经矩阵W解混后对所得u的每个分量ui分别用一个非线性函数gi(ui)进行处理，得:

自适应处理目标函数可调节W使r的总熵量H(r，W)极大，由信息理论知，H(r，W)极大表示u的各分量间互信息I(u1，…，uN)极小。传统Infomax算法中分离矩阵W迭代式为:

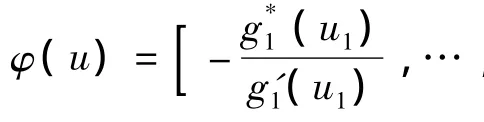
源信号中既有超高斯信号又有亚高斯信号时，采用φ(u)的选择将无法得到满意分离，Lee等［6］在传统Infomax基础上提出扩展的Infomax算法。在信号分离过程中，根据信号峰度变化，转换动态模型系数。分离矩阵调整公式为:

式中:K=diag［sign(k4(u1))，…，sign(k4(uN))］，k4(·)为信号峭度，超高斯情况k4＞0，亚高斯情况k4＜0，输出信号ui峭度可计算如下:

式中:E(·)表示期望，处理过程中可用样本均值进行估计。

过了两天，噩耗传来，水老师病逝了。送葬的人很多，远在上海的蒋海峰也陪父亲来了。他又经历了一次失败的婚姻，还是没有孩子，问题出在自己，他彻底崩溃了。

2 欠定ICA算法

对欠定盲分离问题，大多数算法均在假设源信号稀疏前提下采用聚类或优化算法。该算法对不稀疏信号无能为力;对亚高斯信号缺乏有效欠定盲分离方法。

本文通过生成隐藏数据z，将欠定盲分离问题转化为传统超定盲分离问题，从而应用传统的ICA算法进行分离。隐藏数据z的生成通过最大化已知混叠信号x和解混矩阵W条件概率实现，有:

生成隐藏数据z后，源信号分离问题转化为传统盲源分离问题，如图2所示，新的混叠信号为:

式中:y∈ℝn，z∈ℝn-m。

图2 欠定ICA算法流程图Fig.2 Block diagram of underdetermined ICA

为较好估计隐藏数据z，需较准确估计源信号的概率密度。概率密度估计方法分参数估计与非参数估计。参数估计方法，需假定作为判别依据的、随机取值的数据样本在各个可能的类别中均服从特定分布经验及理论说明，参数模型的基本假定与实际物理模型间常存在较大差距，因此该方法并非总能取得满意结果。鉴于此，Rosenblatt等［7］提出非参数估计方法，即核密度估计方法。由于核密度估计方法不用有关数据分布的先验知识，对数据分布不附加任何假定，从数据样本本身出发研究数据分布特征，因此非常适用于信号盲处理。

给定独立同分布随机变量X的一组实现X1，X2，…，Xn，X的概率密度可估计为:

式中:K(x)称为概率密度函数估计核函数，要求K(x)满足条件:

(1)K(x)对称，即K(x)=K(-x);

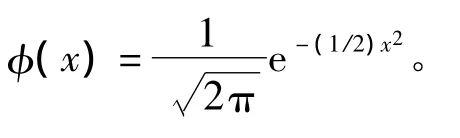
基于扩展Infomax的欠定ICA算法为:

(1)初始化分离矩阵W;

(2)给定观测信号x与分离矩阵W后，据式(10)及当前估计源信号u的核密度估计式(12)由极大似然估计法生成隐藏数据z;

(3)由扩展Infomax算法，式(5)更新分离矩阵W，式(2)估计当前源信号u;

(4)返回步骤(1)直到算法收敛。

3 仿真信号分析

选一标准的Laplace信号作为仿真超高斯源信号s1(t);选s2(t)=sin(40πt)sin(600πt)，s3(t)=sin(200πt)作为仿真两亚高斯源信号，采样点数为1 200，用Matlab产生的随机混合矩阵A对源信号进行混合产生混合信号X=A*［s1;s2;s3］，三个源信号与两路混叠信号波形如图3所示。图4为分离后信号，可以看出，除ICA算法本身固有的分离信号排列顺序及幅值不确定性，信号分离效果较好。

图3 源信号与混叠信号Fig.3 Source signals and mixed signals

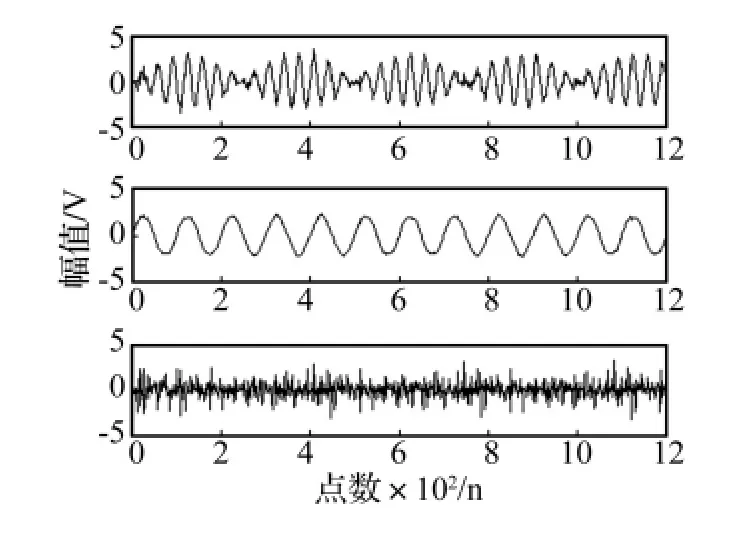
图4 分离信号Fig.4 Separated signals

图5 实测振动信号Fig.5 Vibration signals

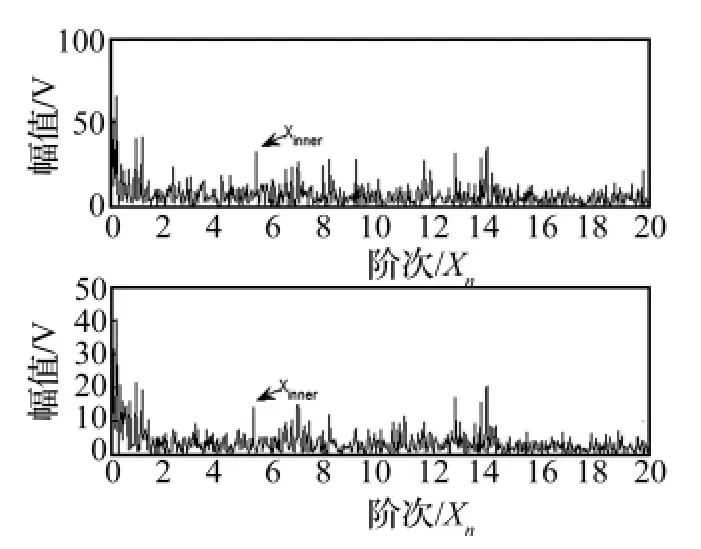
图6 实测振动信号的包络阶次谱图Fig.6 Order envelope spectrum of vibration signals

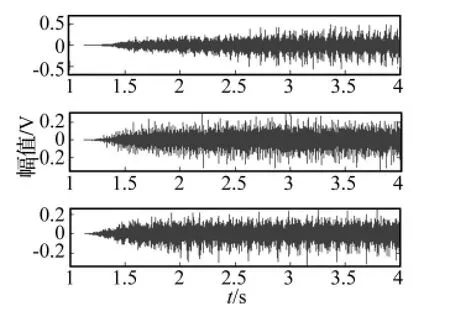
图7 分离信号时域图Fig.7 Separated signals

4 齿轮箱复合故障信号分析

用某型单级齿轮箱进行试验验证。该系统由电机带动输入轴，输出轴带动负载。主动齿轮齿数Z1=30，被动齿轮齿数Z2=50，输入轴轴承为6206型单列向心滚动轴承，输出轴轴承为7207型单列向心滚动轴承，通过在齿轮啮合面切去一定厚度材料模拟齿面磨损故障。轴承故障是在输入轴轴承内圈和滚动体通过线切割实现，对振动信号在时域里进行等时间间隔采样，输入轴转速由0均匀加速1 200 r/min，对加速过程的振动信号进行分离实验。内圈故障特征阶次为Xinner=5.42阶，外圈故障特征阶次为Xouter=3.58阶，滚动体故障特征阶次为Xroller=2.35阶。

由于机械结构振动信号通过结构传递产生延迟，机械系统瞬态特征不会保持不变。但当考虑一刚度很大、位移很小的结构时，其振动传递延迟可忽略不计，可保持瞬态模型。为此，认为齿轮箱振动信号满足线性瞬时混合模型。

在输入轴两端轴承座上各安装一个型号为B＆K4508加速度传感器，两个传感器采集的振动信号时域如图5所示，随转速的提高，信号幅值逐渐增大，此为非稳态过程。由于阶次包络谱［8］能有效提取旋转机械升降速过程中的故障特征阶次，因此本文采用阶次包络谱方法进行分析。实测振动信号阶次包络谱如图6所示，从图中只能看到轴承内圈故障的特征阶次，而外圈及滚动体故障特征却因噪声及混合故障存在变得不明显。

采用本文所提欠定ICA算法对实测振动信号进行处理，分离信号时域图如图7所示，从时域上并不能直观看出分离效果，图8为分离信号包络阶次谱图，从图8(a)、(b)、(c)三幅图中分别可看出内圈、外圈和滚动体故障的特征阶次，说明欠定ICA算法可将三种故障成功分离。

图8 分离信号的包络阶次谱图Fig.8 Order envelope spectrum of separated signals

5 结论

将独立分量分析引入欠定盲分离问题中，解决了欠定情形下超高斯与亚高斯混合信号的分离问题，为欠定盲分离提供了新方法，同时扩展了独立分量分析的应用范围。通过对实测齿轮箱故障信号分析，表明该方法可有效分离齿轮箱故障特征，验证了方法的有效性。

［1］ Li Y，Amari A，Cichocki A.Underdetermined blind source separation based on sparse representation［J］.IEEE Trans Signal Process，2006，54(2):423-437.

［2］ Bofill P，Zibulevsky M.Underdetermined source separation using sparse representations［J］.SignalProcess，2001，81(11):2353-2362.

［3］ Hyvarinen A，Oja E.A fastfixed-pointalgorithm for independent component analysis［J］.Neural Computation，1997，9(7):1483-1492.

［4］ Bell A J，Sejnowski T J.An information-maximization approach to blind separation and blind deconvolution ［J］.Neural Computation，1995，7(6):1129-1159.

［5］ Amari S，Cichochi A.A new learning algorithm for blind source separation［M］.Cambridge:The MIT Press，1996.

［6］ Lee T W，Girolami M，Sejnowski T J.Independent component analysis using an extended infomax algorithm for sub-Gaussian and super-Gaussian sources［J］.Neural Computation，1999，11(2):409-433.

［7］李存华，孙志挥，陈 耿，等.核密度估计及其在聚类算法构造中的应用［J］.计算机研究与发展，2004，41(10):1712-1719.

LI Cun-hua，SUN Zhi-hui，CHEN Geng，et al.Kernel density estimation and its application to clustering algorithm construction［J］.Journal of Computer Research and Development，2004，41(10):1712-1719.

［8］李 辉，郑海起，唐力伟.阶次包络谱在轴承故障诊断中的应用［J］.机械强度，2007，29(3):351-355.

LI Hui，ZHENG Hai-qi，TANG Li-wei.Application of order envelope analysis to bearingfault diagnosis［J］.Journal of Mechanical Strength，2007，29(3):351-355.