周期广义谐和小波变换及重构

孔 凡，李 杰，2

(1.同济大学 土木工程学院，上海 200092;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

小波分析发展历程充分体现出工程与数学领域相互促进关系。小波(wavelet)一词由Morlet等［1］对地震数据分析时提出。Meyer等［2-4］提出连续小波容许性条件及重构公式，并将计算机视觉领域中多尺度分析思想引入小波分析中，提出了多分辨率分析概念及Mallat算法。Daubechies［5］创立了支持离散小波的二进小波理论，并构造出紧支的正交小波基。在小波发展史中，Grossman等［6-7］也做出了杰出贡献。

在完善和发展小波的纯数学理论同时，小波理论在应用数学及工程领域中也颇具前景。Newland等［8］首先将小波分析应用于工程振动信号分析，并提出了谐和小波(Harmonic Wavelet，HW)及广义谐和小波(Generalized Harmonic Wavelet，GHW)概念。HW 与GHW为一类具有解析形式，在频率域上紧支但时域衰减较慢(依t-1)的小波［8-14］。HW被应用在求解常/偏微分方程［15-17］、积分与积分 - 微分方程［18-19］、时频分析［20］、估计随机过程功率谱密度［21-22］以及计算随机激励下系统二阶响应［23-24］等方面。

谐和小波良好的工程应用前景在于其特殊的谐和成分与实际中发生的振动信号结构有相似之处［19］。快速Fourier变换(FFT)技术的应用，使谐和小波变换计算效率更高。HW与GHW均在无穷时域上正交，工程实际中发生的振动信号却不具有无穷持时特征。因此，基于GHW概念，本文提出以有限时间T0为基本周期的周期广义谐和小波(Periodic Generalized Harmonic Wavelet，PGHW);证明了此类小波在有限区间内的正交性;提出了基于FFT的PGHW快速冗余/非冗余小波变换及重构算法，指出了冗余和非冗余小波变换间关系;利用所提小波变换算法，对某地震动时程进行周期广义谐和小波变换及其重构。

1 广义谐和小波

HW与GHW均为具有解析表达、频域紧支且时域衰减很慢的正交复小波［8-10］。其中母小波及尺度函数表达为:

式中:i为虚数单位(除说明显外，正体i为虚数单位，斜体i为下标符号);t为时间。经平移与尺度变换后的HW为:

式中:j为尺度因子;k为平移变换因子，k=2j，2j+1，…，22j-1。

经尺度与平移变换后，HW的Fourier变换为:

式中:Ψ(ω)为母谐和小波的Fourier变换。

尺度函数、母小波函数及经平移与尺度变换后的小波Fourier变换之模见图1。

图1 各级谐和小波的Fourier变换之模Fig.1 Squared modulus of the Fourier transform of HW at different scales

由图1知，谐和小波为二进小波，各级小波频域互不交叠、且逐级宽度加倍高度减倍。如尺度函数频域之模分布于［0，2π)上;0级小波频域之模分布于［2π，4π)上;1级小波频域之模分布于［4π，8π)上;第j级小波频域之模分布于［2j2π，2j+12π)上。每级小波频域宽度为定值，即第j级小波频域宽度为2j2π。因此不具灵活性。为此 Newland［9］提出音乐小波(Musical Wavelet)，也称为GHW。各级GHW的Fourier频宽并不固定为2j2π，而由一对尺度指标确定，即(mj-nj)2π。其中mj，nj为第j级尺度指标。在Newland的原文中，对信号长度进行正规化，因此无论HW或GHW，其各级小波频宽均为2π的倍数(信号长度为T0=1 s)。本文中对GHW采用一般表示方法，即:

式中:i为尺度下标;k=0，1，…，n-m-1为平移变换因子;G表示广义;Δω=2π/T0为信号频域采样间隔;niΔω与miΔω为第i级尺度下小波频域上下限。特别地，可考虑各尺度下小波频带宽相等，即ni-mi=njmj=n-m且ni-1=mi;T0为考虑信号持时。式(5)的GHW在频域内表达为:

各阶GHW在频域内分布见图2。

图2 各阶GHW的Fourier变换模Fig.2 Squared modulus of the Fourier transform of GHW at different scales

2 GHW周期化

据周期化非周期小波的一般过程［5］，周期广义谐和小波可写为:

其中:上标per代表“周期”。

据Fourier变换性质，式(7)右边可写为Fourier变换的逆变换，即:

式(8)右边定义域为mΔω≤ω＜nΔω。据Poisson公式［10，18-19］，有:

式中:δ(ω-qΔω)为函数。当l=π/T0时，式(9)可化为:

结合式(8)与式(10)知:

因此，PGHW可写为:

容易证明，式(12)频域表达为:

由式(12)知，周期广义谐和小波在时域上表现为若干谐和项之和;且平移因子表现为谐和项相位滞后;在频域上表现为若干δ函数之和，且其中每个δ函数坐落于此尺度的频域区间内每个频率采样点处。与GHW相同，PGHW为复小波，其实部为偶函数虚部为奇函数。式(12)中，平移变换因子k=0，1，…，n-m-1，PGHW平移一次，实际在时域上平移了T0/(n-m)。可以证明，平移后的PGHW在基本周期［0，T0)内是正交的。

如果使PGHW每平移一次，在时域上表现为平移了Δt，Δt为时间取样间隔。则式(12)可改写为:

式中:k=0，1，…，N-1为平移变换因子，N为时间取样总数。式(14)可称为冗余PGHW。可证，平移后的PGHW在基本周期上并非两两正交。

图3为在某尺度与平移因子下且基本周期为T0=20.48 s的正交PGHW。由图3知，PGHW的实部与虚部分别为关于其基本周期内中点的偶函数与奇函数。尺度因子越大，振动频率越高。

图3 正交(t)，(t)，(t)(t)小波的实部(实线)与虚部Fig.3 Real and imaginary part of orthogonal PGHW，(t)(t)(t)(t)

据PGHW频域简单性，易证式(12)PGHW在其基本周期［0，T0)上是正交的，即:

其中:〈·〉为函数内积符号，且:

由于PGHW的正交性，可保证其完全重构性(Perfect Reconstruction)。

3 变换与重构

根据定义，正交PGHW的小波变换可写为:

结合式(12)，式(17)可写为:

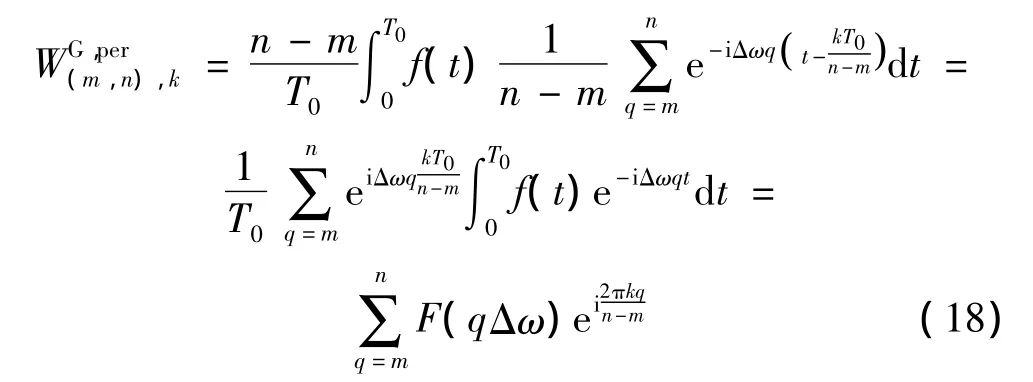
据式(18)，正交PGHW变换见图4。

图4 f(t)正交PGHW的小波变换Fig.4 Flow chart of the fast orthogonal PGHW transform

当原始信号为复值信号时，其重构公式为:

以工程教育认证为指导纲要,在培养社会所需人才的模式和方法上,突出工程应用教育的特点,强调“三结合”(理论与实践结合、课内与课外结合、学校与企业结合),坚持系统更新优化、稳中求新、求进的原则,考虑社会发展、技术革新、需求引导、市场反馈意见等多方面因素,从而形成持续改进的测控技术与仪器专业人才培养模式。

式中:Re表示求实部。

数值试验表明，利用式(21)、式(12)进行PGHW小波逆变换，由于循环求和原因，计算效率不佳。利用FFT技术，可加快PGHW小波变换速度。考察PGHW周期性后，本文提出快速PGHW逆变换算法。式(19)可表达为:

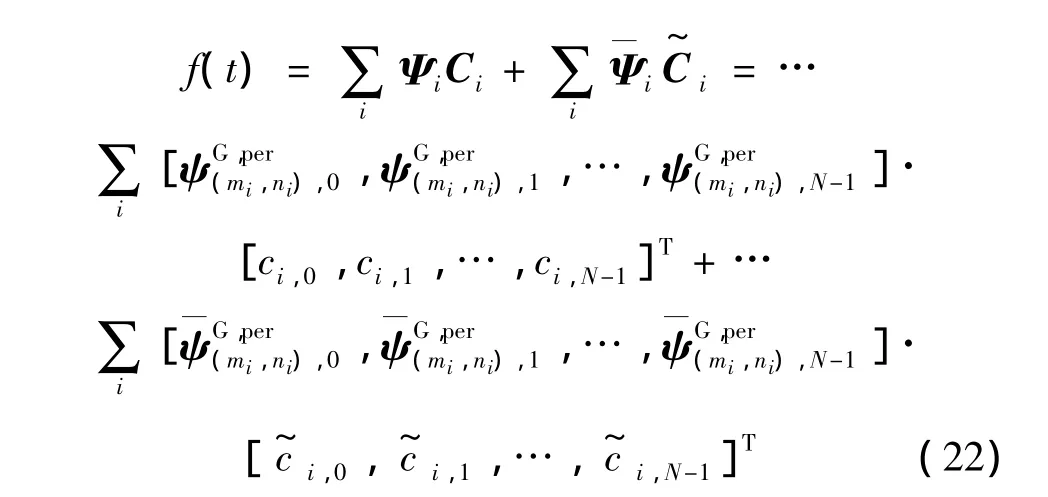
式中:N为时间取样总点数。

式中:t1，t2，…，tN为时间取样点，)，k为的复共轭。

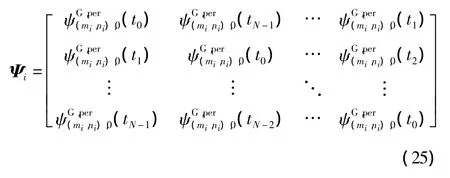
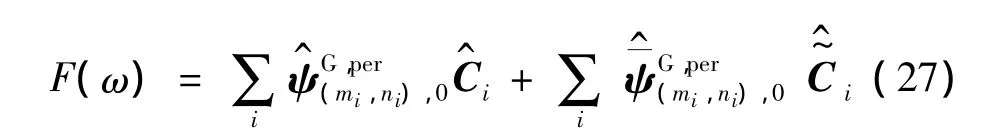
同理，式(14)的非正交小波可变换为:

图5 快速正交PGHW重构算法Fig.5 Flow chart of the fast reconstruction algorithm of orthogonal PGHW

将式(14)代入式(28)得:

非正交PGHW的小波变换见图6。

图6 f(t)非正交PGHW的小波变换Fig.6 Flow chart of the fast redundant PGHW transform

非正交PGHW的小波逆变换也可表达为式(19)、式(21)形式，区别在于该小波变换表达式为式(28)且:

式中:k=0，1，…，N-1为时间平移因子。

虽然快速非正交PGHW的小波重构算法与快速正交PGHW的小波重构算法类似，但区别为无图5中上插值(Upsampling)环节。

显然，式(12)小波在基本周期上构成一完备正交系，小波之间两两正交，称其小波变换为非冗余小波变换。式(14)小波集合包含式(12)小波集合，称其小波变换为冗余小波变换。非冗余小波变换为与离散信号同维向量;而冗余小波变换为矩阵，其中每个尺度下冗余小波变换为矩阵中的某一向量。即，非冗余小波变换与原始信号之间所包含的信息相等，当且仅当有该非冗余小波变换时，即可完全重构原始信号;而冗余小波变换中所包含信息大于原始信号中信息。因此，非冗余小波变换较冗余小波变换更高效，但重构原始信号时，前者较后者对误差更敏感。由于冗余小波的光滑性(图7)，在利用PGHW估计随机过程功率谱应用中，较正交非冗余PGHW更具优势。对比式(18)与式(28)，二者之关系为:

4 数值算例

以非平稳地震动时程为例，利用所提非冗余及冗余PGHW变换的快速算法，进行时程样本的小波变换及重构。平稳随机地震动功率谱采用Kanai-Tajimi谱，即:

式中:ωs，ζs为场地卓越频率及等效阻尼;S0为基岩输入白噪声幅值。

地震动非平稳性由包络函数表达，即:

式中:g(t)为包络函数;S0分别为平稳随机过程与非平稳随机过程样本函数;α=0.25，β=0.5为包络函数参数;k为使gmax(t)=1的正规化系数。

目标非平稳地震动时程样本由式(32)及平稳谱表达方法［25-26］(Spectral Representation Method)生成。

图7为样本地震动在某尺度下的非冗余及冗余小波变换，二者之关系见式(31)。图8为目标非平稳地震动时程与非冗余PGHW快速小波重构后的非平稳时程对比。利用冗余PGHW快速小波重构算法也可得到类似结果。由图8可见，小波变换后重构信号与原信号吻合良好，说明本文所提PGHW快速小波变换与重构算法的可靠性。

图7 某样本地震动在某尺度下非冗余及冗余小波变换Fig.7 Non-redundant and redundant PGHW transform of an earthquake excitation at a certain scale

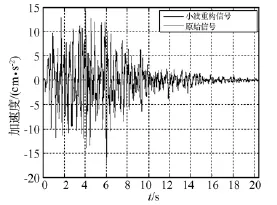
图8 样本目标地震动与重构地震动对比Fig.8 Comparison between the original and the reconstructed signal

5 结论

(1)本文提出在基本周期［0，T0)内正交的谐和小波，即周期广义谐和小波(PGHW)。PGHW母小波可看作经若干谐和分量叠加而得;不仅保留了谐和小波族在频域内的简单性，且非冗余PGHW在基本周期［0，T0)上正交。

(2)本文给出基于快速Fourier变换的快速正交(非冗余)PGHW变换与冗余PGHW变换及相应的快速逆变换，指出冗余及非冗余小波变换之间的关联性。数值算例表明，由于PGHW在有限区间内的正交性，保证了其在相应区间内的完全重构性。

［1］ Grossmann A，Morlet J.Decomposition of Hardy function into square intergrable wavelets of constant shape［J］.Journal on Mathematical Analysis，1984，15:723-736.

［2］Meyer Y.Principe d’incertitude，bases hilbertiennes et algebres d’opérateurs［J］.Seminaire Bourbaki，1985，622:1985-1986.

［3］Meyer Y.Ondelettes et operateurs，I.Ondelettes［M］.Paris:Hermann，1990.

［4］Mallat S. Multiresolution approximations and wavelet orthonormal bases of L2(R)［J］.Transactions of the American Mathematical Society，1989，315(1):69-87.

［5］Daubechies I.Ten lectures on wavelets［M］.Philadelphia:Society for Industrial and Applied Mathematics，1992.

［6］Coifman R R.Wavelet analysis and signal processing，signal processing part I［M］.Springer-Verlag，1990:59-68.

［7］Chui C K.An introduction to wavelets［M］.San Diego:Academic Press Professional，Inc，1992.

［8］ Newland D E.An introduction to random vibrations，spectral and wavelet analysis［M］.New York:Longman Scientific＆Technical，1993.

［9］Newland D E.Harmonicandmusicalwavelets ［J］.Proceedings of the Royal Society of London.Series A:Mathematical and Physical Sciences，1994，444(1922):605-620.

［10］ Newland D E.Harmonic wavelet analysis［J］.Proceedings of the Royal Society of London.Series A:Mathematical and Physical Sciences，1993，443(1917):203-225.

［11］ Newland D E.Ridge and phase identification in the frequency analysis of transient signals by harmonic wavelets ［J］.Journal ofVibrationandAcoustics， 1999， 121(2):149-155.

［12］ Newland D E.Practical signal analysis:do wavelets make any difference?［A］.Proceedings of the 16th ASME Biennial Conference on Vibration and Noise.Sacramento，1997.

［13］ Newland D E.Wavelet analysis of vibrations，part II:wavelet maps ［J］.Journal of Vibration and Acoustics，1994，116(4):417-425.

［14］ Newland D E.Wavelet analysis of vibration，part I:theory［J］.Journal of Vibration and Acoustics，1994，116(4):409-416.

［15］Muniandy S V，Moroz I M.Galerkin modelling of the burgers equation using harmonic wavelets［J］.Physics Letters A，1997，235(4):352-356.

［16］ Cattani C.The wavelet-based technique in dispersive wave propagation ［J］.International Applied Mechanics，2003，39(4):493-501.

［17］ Cattani C. Harmonic waveletstowardsthe solution of nonlinear PDE ［J］.Computers and Mathematics with Applications，2005，50(8-9):1191-1210.

［18］ Cattani C，Kudreyko A.Harmonic wavelet method towards solution of the fredholm type integral equations of the second kind ［J］.Applied Mathematics and Computation，2010，215(12):4164-4171.

［19］Cattani C，Kudreyko A.Application of periodized harmonic wavelets towards solution of eigenvalue problems for integral equations ［J］.Mathematical Problems in Engineering，2010，2010:570136-570143.

［20］ Spanos P，Giaralis A，Politis N.Time-frequency representation of earthquake accelerograms and inelastic structural response recordsusing the adaptive chirpletdecomposition and empirical mode decomposition ［J］.Soil Dynamics and Earthquake Engineering，2007，27(7):675-689.

［21］ Spanos P D，Tezcan J，Tratskas P.Stochastic processes evolutionary spectrum estimation via harmonic wavelets［J］.Computer Methods in Applied Mechanics and Engineering，2005，194(12-16):1367-1383.

［22］ Tratskas P. Wavelet-based excitation Representation and response determination of linear and nonlinear systems［D］.Houston:Rice University，2001.

［23］Spanos P D，Kougioumtzoglou I A.Harmonic wavelets based statisticallinearization for response evolutionary power spectrum determination ［J］. Probabilistic Engineering Mechanics，2012，27(1):57-68.

［24］ Tratskas P， Spanos P D. Linear multi-degree-offreedomsystem stochastic response by using the harmonic wavelet transform［J］.Journal of Applied Mechanics，2003，70(5):724-731.

［25］Liang J W，Chaudhuri S R，Shinozuka M.Simulation of nonostationary stochastic process by spectral representation［J］.Journal of Engineering Mechanics，2007，133(6):616-627.

［26］Shinozuka M.Simulation of stochastic processes by spectral representation［J］.Applied Mechanics Reviews，1991，44(4):191-204.