卷积型小波变换实现及机械早期故障诊断应用

罗 荣，田福庆，李克玉，丁庆喜

(海军工程大学 兵器工程系，武汉 430033)

机械故障诊断领域中通常采用内积型小波变换，并利用Mallat算法实现其快速运算。但Mallat算法用于机械故障诊断存有缺陷:① 该算法引入下采样环节使分解长度随分解层数的增加依次减半，从而使概貌信号信息量减少，时间分辨率降低，不利于机械故障特征提取［1］。若对Mallat算法分解后的频带进行单支重构，不仅会增加计算量，还会使信号产生畸变［2-3］。②任何实际滤波器组的幅频特性与理想幅频特性有一定差距使各滤波器频带有一定重叠及Mallat算法特有的上下抽样环节，共同造成Mallat算法分解后的子带存在频率折叠，并非原信号的真实分量，会影响分析结果的可读性，频率折叠严重时还会造成误判［4-6］。

为消除Mallat算法固有缺陷对机械故障特征提取的不利影响，更好应用小波变换进行机械故障诊断，文献［4-5］提出单子带重构改进算法，用FFT滤波原理强制型去掉多余频率成分;文献［6］提出的巴特沃斯小波变换算法基于性能优良的巴特沃斯滤波器组实现无下抽样环节的小波变换快速算法。本文提出摒弃内积型小波变换，采用卷积型小波变换进行机械故障诊断。基于此，本文首先推导出卷积型小波变换快速分解算法，并给出基于滤波器组的递归分解实现方法。与Mallat算法相比，该快速算法不存在隔点取样过程，只对上一尺度分解结果进行移位，无论信号被分解多少层，每层分解所得逼近信号与细节信号长度始终与原始信号一致。因此该快速算法进行故障特征提取无须单子带重构过程，计算量少，便于工程实现。更重要的是，由于不存在隔点取样过程，该快速算法分解所得各子带信号为信号的真实分量，不存在频率折叠，有利于提取故障特征。可见，卷积型小波变换完全克服了内积型小波变换不利于机械故障诊断问题。文献［7］通过详地比较认为卷积型小波变换对信号的处理效果优于内积型小波变换，不仅频带分离效果较内积型小波变换优越，且所提故障特征信息也较内积型小波变换明显。因此卷积型小波变换更适合机械故障特征提取。

针对滚动轴承早期故障诊断与定量识别难题与共振解调法、冲击脉冲法的不足，本文提出将卷积型小波变换与共振解调法、冲击脉冲法相结合的新方法对滚动轴承早期故障进行诊断与定量识别，并给出具体实现过程。仿真实验与实例分析表明，卷积型小波变换能消除Mallat算法对机械故障特征提取的不利影响，用于机械故障诊断较内积型小波变换优势明显。本文所提新方法可有效实现对滚动轴承早期故障诊断与定量识别，具有一定应用价值。

1 卷积型小波变换及快速分解算法

设{Vj}j∈Z为空间L2(R)的正交多分辨率分析，φ(x)∈V0为{Vj}j∈Z的正交尺度函数，φ(x)∈W0为{Vj}j∈Z的正交小波函数，Wj为Vj在Vj-1中的正交补。由于Vj⊂Vj-1，Wj⊂Wj-1，所以Vj中元素 2-j/2φ(2-jx)与Wj中元素2-j/2ψ(2-jx)可分别用Vj-1的基表示:

设f(t)∈L2(R)，记ψ(t)以s为尺度的扩张函数为:ψs(t)=1/sψ(t/s)，则f(t)与ψs(t)的卷积型连续小波变换定义为［8］:

令s=2j，x=k2j得:

可证明Wjf(k)与内积型小波系数仅相差一个常数，故Wjf(k)即f(t)在Wj中的系数。

记φ(t)以s为尺度扩张函数为:φs(t)=1/sφ(t/s)，且Ssf(x)=f(t)*φs(t)，再令s=2j，x=k2j，则有:

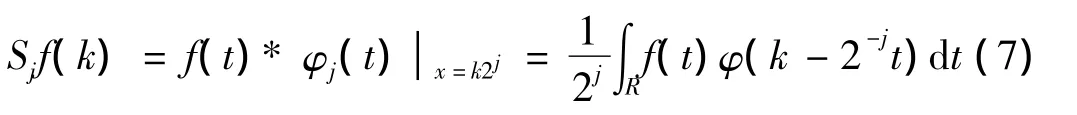
同样可证明Sjf(k)与内积型小波系数也仅相差一个常数，故Sjf(k)即f(t)在Vj中的系数。

1.1 卷积型小波变换快速分解算法推导

对Sjf(x)=f(t)*φj(t)等号两边对x求傅氏变换并将式(3)代入得:

将上式转换到时域得:

令x=k2j得:

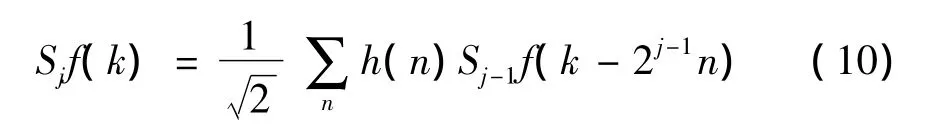
同理对细节系数有:

式(10)、(11)即为卷积型小波变换的快速分解算法，可采用基于滤波器组的递归分解方法实现。实现过程为:

对式(10)等号两边同时进行z变换得:

同理:

式中:Wjf(k)为Sj-1f(k)通过滤波器1/G(z2j-1)后的输出，G(z2j-1)由滤波器G(z)每两点间插入2j-1-1个零所得。卷积型小波变换快速分解算法基于滤波器组的递归分解实现方法见图1。

2 仿真实验

通过两个仿真实验比较两类小波变换对信号的处理效果。

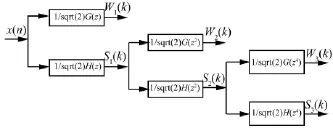
图1 卷积型小波变换快速分解算法基于滤波器组的递归分解实现方法Fig.1 The recursion realization of the fast decomposition algorithm of convolution type of wavelet transformation based on filter banks

2.1 两类小波变换对多频信号分解效果比较

设时间信号y(t)的表达式为:

即信号y(t)包含15 Hz，30 Hz，60 Hz，80 Hz，100 Hz，120 Hz，150 Hz等七个频率成分。以512 Hz采样率对此信号采样512点，分别利用卷积型小波变换快速分解算法与Mallat算法对采样信号进行3层分解，所用小波均为db40小波，分解频谱比较如图2所示。信号y(t)的小波分解得到的各子带理论上的频率成分如表1所示。为便于比较，图2内积型小波分解频谱为单支重构频谱。由图2看出，卷积型小波变换所得各子带无任何虚假频率，为信号的真实分量，只因小波滤波器的非理想频域截止特性造成子带含相邻子带部分频率成分。此因任何实际滤波器均不具有理想频域截止特性所致。而Mallat算法分解所得子带信号，不仅含相邻子带部分频率成分，且存在频率折叠，出现明显的虚假频率成分，如W1子带 136 Hz，W2子带 68 Hz，S3子带34 Hz等。虚假频率混在子带信号中可致子带信号发生畸变。如图3中内积型小波分解所得近似子带S3提取的二倍频信号出现明显畸变，远不及卷积型小波变换提取的清晰，此因内积型小波分解所得近似子带S3中混有频率34 Hz，幅值0.36的虚假成分所致。此仿真实验说明Mallat算法用于信号分解会产生严重频率折叠，所得子带信号并非信号的真实分量，不利于机械故障特征提取。而卷积型小波变换用于信号分解则不会产生任何频率折叠，完全克服了Mallat算法产生频率折叠缺陷。

表1 各子带理论频率成分Tab.1 Frequencys of bands under ideal conditions

图2 两类小波变换所得子带频谱比较Fig.2 The comparison between bands spectrums of two types of wavelet transformation

图3 两类小波变换所得近似子带S3比较Fig.3 The comparison between approximate bands of two types of wavelet transformation

2.2 两类小波变换对多载波调幅信号各调幅波及调制信息提取效果比较

由于轴承故障振动信号大多由复杂的具有多载波与多调制的调幅波，从中提取各调幅波并进行包络解调即可提取故障特征信息进行故障诊断。设多载波调幅信号为:

对式(15)信号以512 Hz采样率采样512点，如图4所示。① 分别利用卷积型小波变换快速分解算法与Mallat算法对该信号进行2层分解(用db40小波)，分解结果及频谱如图5、图6所示。② 分别对两类小波变换的分解结果进行希尔伯特解调，所得包络及包络谱如图7、图8所示。比较图5、图6可知，卷积型小波变换分解所得各子带未产生虚假频率，较完美地提取出各调幅波;而Mallat算法分解所得子带则有明显虚假频率，以致其对各调幅波的提取效果不及卷积型小波变换。比较图7、图8可知，卷积型小波变换分解结果包络基本与各调幅波真实包络一致，而内积型小波变换分解结果包络较粗糙并与真实包络相差较大，甚至包络谱中出现虚假谱峰。因此，卷积型小波变换对多载波调幅信号各调幅波及调制信息的提取效果好于内积型小波变换。此仿真实验说明Mallat算法产生的频率折叠会影响内积型小波变换对各调幅波及调制信息的准确提取，不利于机械特征提取。

由以上两仿真实验可知，卷积型小波变换分解所得子带是信号的真实分量，无频率折叠;内积型小波变换所得子带则存在严重频率折叠。频率折叠严重时必会影响故障特征提取，导致机械故障诊断困难，甚至会造成误诊。故卷积型小波变换较内积型小波变换更适合机械故障诊断。

图4 多载波调幅信号及其频谱Fig.4 The amplitude modulation signal and its spectrum

图5 卷积型小波变换后各子带信号及频谱Fig.5 The results of convolution wavelet transformation and their spectrums

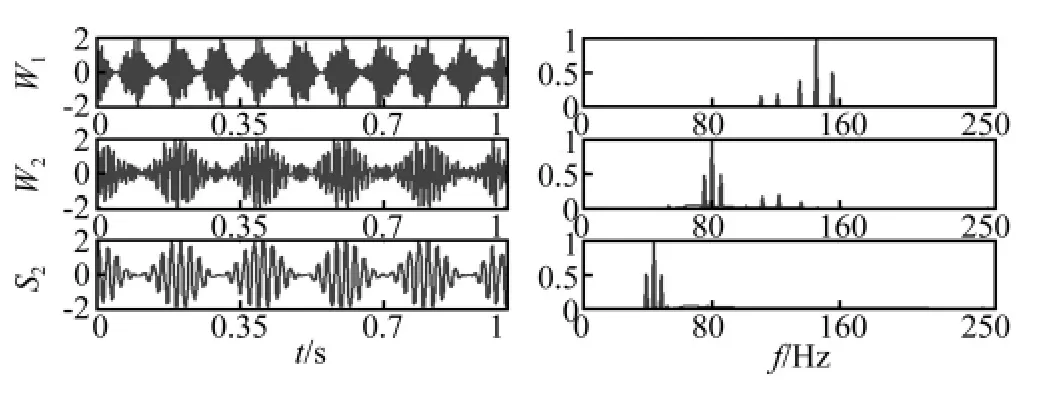
图6 内积型小波变换后各子带及频谱Fig.6 The results of traditional wavelet transformation and their spectrums

图7 卷积型小波变换后各子带包络及包络谱Fig.7 The envelopes of results of convolution wavelet transformation and their spectrums

图8 内积型小波变换后各子带包络及包络谱Fig.8 The envelopes of results of traditional wavelet transformation and their spectrums

3 滚动轴承早期故障诊断与定量识别新方法提出

滚动轴承运转中会因各种原因导致其过早损坏，如装配不当、润滑不良、水分及异物侵入、腐蚀等。即使安装、润滑及使用维护正常，经过一段时间运转也会出现疲劳剥落及磨损而不能正常工作。因此，对滚动轴承早期故障进行诊断、准确判定其损伤的严重程度，预防重大事故发生，成为故障诊断领域中重要研究方向［9］。

共振解调法可将轴承缺陷信息从复杂的调幅振动中分离出来，是目前滚动轴承故障诊断中常用方法之一。共振解调技术关键在于带通滤波的实现。但传统的共振解调技术中，通常采用单一带通滤波器滤除混杂在信息中的无用成分以提高信噪比。主要问题有:① 传统带通滤波器参数选择取决于操作者经验及历史数据，获得满意结果前需多次尝试，费时费力［10］;②滚动轴承发生故障时，通常不止一个载波频率，用单一带通滤波器进行包络分析，难全面提取隐含在振动信号各调制频带内的故障信息特征，甚至包络谱中出现非故障特征频率的谱峰。因此，传统的共振解调技术对滚动轴承中晚期故障诊断虽有一定效果，但不适合滚动轴承早期故障诊断［9］。

冲击脉冲法是另一种简单适用的滚动轴承故障检测方法由瑞典SPM公司提出，被公认为对诊断滚动轴承局部损伤故障工程实用性最强的方法［11］。滚动轴承各元件存在缺陷时，在运转过程中损伤点会反复快速撞击与之接触的其它元件表面而发生冲击，引起脉冲性振动。冲击脉冲的强弱代表故障的严重程度，因此冲击脉冲的大小可用于对故障程度进行定量识别。冲击脉冲法即通过检测冲击点处的冲击波幅值判定轴承工作状态及定量识别故障程度［9，11］。然而，冲击脉冲值不仅与轴承的油膜厚度、操作程度有关，且与轴承几何尺寸及转速有关。为得到衡量各种滚动轴承状态标准，SPM公司规定了只与轴承工作状况有关的标准分贝值，即表示冲击值的增加率，并给出标准分贝值的经验计算公式［9，12-13］:

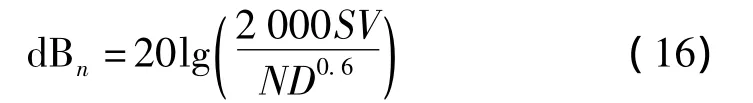
式中:dBn为标准分贝值;N为轴转速(r/min);D为轴承内径(m);SV为冲击值(m/s2)。轴承运转过程中最大标准分贝值dBn，max即可定量识别故障程度。实践证明，对稳态运行设备，评定各类轴承的工作状态的dBn，max为:

(1)0 dB≤dBn，max≤21 dB 正常状态，轴承工作状态良好;

(2)21 dB≤dBn，max≤35 dB 轻微故障，轴承早期损伤;

(3)35 dB≤dBn，max≤60 dB 严重故障，轴承已有明显损伤。

冲击脉冲法可有效判定轴承工作状态及准确定量识别故障，却不能确定故障具体位置。卷积型小波变换与内积型小波变换相同，为较精细的小波分解方法，具有良好时频局域化功能及优良带通滤波功能，无须重构过程，便于工程实现，分解的各子带信号不存在频率折叠，具有较内积型小波变换更好的频带分离特性。因此，为弥补共振解调法与冲击脉冲法不足，实现故障的准确定位与定量识别，本文将卷积型小波变换引入共振解调法与冲击脉冲法中，提出将卷积型小波变换与共振解调法、冲击脉冲法相结合的新方法对滚动轴承早期故障进行诊断与定量识别，具体过程如下:

(1)将原始振动信号按卷积型小波变换快速分解算法进行分解;

(2)将分解所得各子带进行Hilbert包络解调得各子带包络，对包络进行快速FFT变换得各个子带包络谱，即可从中提取滚动轴承早期故障特征，从而定位故障到具体元件;

(3)将各子带包络谱幅值作为冲击值代入式(16)计算标准分贝值，提取各子带故障特征频率处对应的标准分贝值;

(4)选取各子带中同一故障特征频率对应标准分贝值的最大值dBn，max，对滚动轴承故障进行定量识别。

4 实例分析

据实验台实验数据，实验时用电火花制造支撑轴承外圈点蚀损伤模拟早期微弱损伤故障，为支撑轴承座加垫片模拟平行不对中故障。支撑轴承为6205深沟球轴承，几何参数为:轴承节径39.04 mm，滚动体直径7.94 mm，滚动体9个，接触角0°。实验时轴转频约29 Hz。据上述参数计算出外圈故障特征频率为103 Hz。实验数据采样频率8 kHz，数据长度为8 192点，数据单位为10 m/s2。

4.1 两类小波变换对外圈故障特征提取效果比较及故障定量识别

图9为所测故障振动信号及频谱。对此故障振动信号分别进行4层卷积型小波分解与内积型小波分解，所用小波均为db40。卷积型小波分解所得细节子带W1，W2，W3的包络谱与内积型小波分解所得细节子带W1，W2，W3的包络谱比较见图10。由图10知，卷积型小波分解所得细节子带W1，W2，W3的包络谱在外圈故障特征频率103 Hz及2，3，4倍频处均出现明显谱线，而内积型小波分解所得细节子带W1，W2，W3的包络谱仅在外圈故障特征频率103 Hz及2倍频处出现明显谱线。说明卷积型小波提取的外圈故障特征好于内积型小波。卷积型小波分解所得细节子带W1，W2，W3的包络谱分贝值见图11。由图11知，卷积型小波分解各子带外圈故障特征频率及倍频对应的分贝值最大为25.61 dB。说明滚动轴承外圈存在早期损伤故障。因此本文提出的卷积小波包络解调方法可有效诊断并定量识别滚动轴承早期故障。

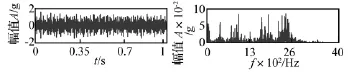
图9 振动信号及频谱Fig.9 The vibration signals and its spectrum

4.2 两类小波变换对不对中故障特征提取效果比较

对此故障信号分别进行6层卷积型小波分解与内积型小波分解，所用小波均为db40。卷积型小波与内积型小波分解所得第6层近似子带S6及频谱见图12、图13。由图12知，卷积型小波分解所得子带S6为基频分量29.3 Hz与二次谐波分量57.62 Hz的叠加。说明经卷积型小波“去粗存精，层层剥离”分解，所得近似信号即“骨架”较清楚地提取到不对中故障的两倍频振动现象。由图13可知，内积型小波提取的两倍频振动现象明显不及卷积型小波提取到的清晰。因为内积型小波分解所得子带S6中存在虚假频率成分67.38 Hz。此虚假频率经分析发现由Mallat算法中隔点插零环节由频率折叠所致。67.38 Hz即为二次谐波分量57.62Hz关于S6子带理论上最大频率62 Hz的映像，该映像经重构低通滤波器后未完全滤掉而留在S6子带中。由此可见，小波滤波非理想特性及Mallat算法上下抽样环节共同造成了Mallat算法中的频率折叠;而卷积型小波无上下抽样环节，不会产生频率折叠，且分解后的频带无须重构。故卷积型小波变换无上下抽样环节使其在机械故障诊断中较内积型小波变换更具优势。

图10 两类小波变换后各子带包络谱比较Fig.10 The comparison between bands envelope spectrums of two types of wavelet transformation

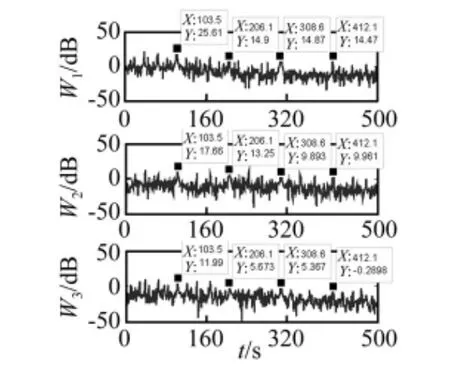
图11 卷积型小波变换后各子带包络谱分贝值图Fig.11 The dB values of bands envelope spectrums of convolution wavelet transformation

图12 卷积型小波变换后子带S6及其频谱Fig.12 The band S6 of convolution wavelet transformation and its spectrum

图13 内积型小波变换后子带S6及其频谱Fig.13 The band S6 of traditional wavelet transformation and its spectrum

5 结论

(1)与内积型小波变换相比，卷积型小波变换无须重构过程，便于工程实现，分解的各子带不存在频率折叠，具有较内积型小波变换更好的频带分离特性，可消除Mallat算法存在频率折叠等固有缺陷对机械故障诊断的不利影响。

(2)采用卷积型小波变换进行机械故障诊断，推导出卷积型小波变换快速分解算法，给出基于滤波器组的递归分解实现方法。

(3)提出的将卷积型小波变换与共振解调法、冲击脉冲法相结合的新方法及具体实现过程，弥补了滚动轴承早期故障诊断与定量识别难题及共振解调法、冲击脉冲法的不足。

(4)卷积型小波变换能消除Mallat算法存在频率折叠等固有缺陷对机械故障诊断的不利影响，用于机械故障诊断较内积型小波变换更有优势。本文所提新方法可有效实现对滚动轴承早期故障诊断与定量识别，具有一定工程应用价值。

［1］万书亭，吕路勇，何玉灵.基于提升模式非抽样小波变换的滚动轴承故障诊断方法研究［J］.振动与冲击，2009，28(1):170-173.

WAN Shu-ting，LÜ Lu-yong，HE Yu-ling.Fault diagnosis method of rolling bearing based on undecimated wavelet transformation of lifting scheme［J］.Journal of Vibration and Shock，2009，28(1):170-173.

［2］ Zhao X Z，Ye B Y.Convolution wavelet packet transform and its applications to signal processing［J］.Digital Signal Processing，2010，20(5):1352-1364.

［3］张兆伟，陈维义，林春生.一种对称小波重构算法及其在突变信号检测中的应用［J］.武汉理工大学学报(交通科学与工程版)，2005，29(6):685-688.

ZHANG Zhao-wei，CHEN Wei-yi，LIN Chun-sheng.Symmetric wavelets based non-distortion decomposition and reconstruction algorithm［J］.Journal of Wuhan University of Technology(Transportation Science ＆Engineering)，2005，29(6):685-688.

［4］ Yang J G，Park S T.An anti-aliasing algorithm for discrete wavelet transform ［J］.Mechanical Systems and Signal Processing，2003，17(5):945-954.

［5］杨建国.小波分析及其工程应用［M］.北京:机械工业出版社，2005:47-55.

［6］何岭松，王峻峰.巴特沃斯小波变换算法在故障诊断中的应用［J］.华中理工大学学报，2000，28(10):31-33.

HE Ling-song WANG Jun-feng.Butterworth based on discrete wavelettransform and itsapplication in machine fault diagnosis［J］.J.Huazhong Univ.of Sci.＆ Tech，2000，28(10):31-33.

［7］赵学智，陈统坚，叶邦彦，等.内积型和卷积型小波变换对信号处理效果的研究［J］.机械工程学报，2004，40(3):55-60.

ZHAO Xue-zhi，CHEN Tong-jian，YE Bang-yan，et al.Research on signal processing effect of both inner product type of wavelet transformation and convolution type of wavelet transformation［J］.Chinese Journal of Mechanical Engineering，2004，40(3):55-60.

［8］秦前清，杨宗凯.实用小波分析［M］.西安:西安电子科技大学出版社，1995.

［9］何正嘉，訾艳阳，张西宁.现代信号处理及工程应用［M］.西安:西安交通大学出版社，2007.

［10］苏文胜，王奉涛，张志新，等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用［J］.振动与冲击，2010，3(29):18-21.

SU Wen-sheng，WANG Feng-tao，ZHANG Zhi-xin，et al.Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings［J］.Journal of Vibration and Shock，2010，3(29):18-21.

［11］黄 海，王晓萍，张卫东.冲击脉冲法评价滚动轴承故障的系数自修正方法［J］.机械工程学报，1999，35(2):85-87.

HUANG hai，WANG Xiao-ping，ZHANG Wei-dong.Parameter self-modification method for SPM using in rolling bearing fault diagnosis［J］.Chinese Journal of Mechanical Engineering，1999，35(2):85-87.

［12］姜洪开，王仲生.第二代小波包构造及发动机微弱损伤识别［J］.北京航空航天大学学报，2007，33(7):777-780.

JIANG Hong-kai，WANG Zhong-sheng.Second generation wavelet packet construction and aircraft engine weak damage identification［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(7):777-780.

［13］徐玉秀，原陪新，王占国.冲击脉冲法在电机轴承故障诊断中的应用［J］.沈阳工业大学学报，2000，22(6):453-455.

XU Yu-xiu，YUAN Pei-xin，WANG Zhan-guo.Application of shock impulse method on motor bearing fault diagnosis［J］.Journal of Shenyang University of Technology，2000，22(6):453-455.