基于概率地震需求分析的铅芯橡胶支座抗震性能研究

李 圣，钟铁毅，张常勇

(北京交通大学 土木建筑工程学院，北京 100044)

地震是强随机性事件。但长期以来，限于对地震了解与计算方法不足，多习惯于研究结构对确定地震时程响应进行确定性抗震分析。随着基于性能抗震设计(Performance-Based Earthquake Engineering，PBEE)方法取得进展及推广运用，越发意识到用确定性分析方法评价结构抗震性能的不足。

桥梁减隔震设计中，铅芯橡胶支座运用广泛。大多数研究通过对确定地震时程分析结果进行简单统计研究支座隔震效果。本文据太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center，PEER)提出的基于一致可靠度概率评价思想，从概率地震需求角度研究铅芯橡胶支座的隔震性能。

1 概率地震需求分析(PSDA)概述

基于性能的地震工程要求设计能准确描述结构在特定地震危险环境下的失效概率，通过特别设计使结构达到预期目标。为实现对基于性能的地震工程进行全面概率分析，PEER提出基于一致可靠度的概率决策框架［1-2］，通过将问题分解为易求解的模块，得到不同社会经济决策指标(Socio-economic Decision Variables，DV)的年超越概率。其模块分别为:场地危险性分析、概率地震需求分析、概率地震损伤分析、概率地震损失分析与决策。其中，概率地震需求分析(Probabilistic Seismic Demand Analysis，PSDA)是为估计在某特定地震危险环境下结构需求参数达到不同数量等级的超越概率。概率地震需求分析包括三部分:① 建立结构概率地震需求模型(Probabilistic Seismic Demand Model，PSDM);② 得到结构对特定破坏状态的易损性(Fragility)，即概率地震易损性分析(PSFA);③ 得到结构在特定地震环境下的危险性(Hazard)，即需求危险性分析(PSDHA)。其中场地危险性分析(PSHA)为需求危险性分析前期工作。

针对概率地震需求分析，Shome等［3］阐述了建立非线性结构概率地震需求模型方法;Kevin等［2，4］对美国加州高速公路跨线桥建立了概率地震需求模型，并进一步分析了基于性能抗震设计的桥梁地震需求;Nielson等［5］对高速公路桥梁进行了概率地震易损性分析;Zhang［6］用概率方法对一完整桥梁结构性能进行了评价;陈亮等［10］研究了地震持时对钢筋混凝土桥墩地震需求影响;吕大刚等［11］对概率地震需求分析的云图法进行了改进。

1.1 概率地震需求模型(PSDM)

概率地震需求模型通过求解地震强度(Intensity Measure，IM)及工程地震需求参数(Engineering Demand Parameter，EDP)之间的条件相关性，即GEDP|IM，表征结构自身抗震性能。其中地震强度IM可为地震烈度(MW)，或地震动峰值(PGA，PGV，PGD)，或结构对应的地震动反应谱值(Sa，Sv，Sd)等参数;地震需求参数(EDP)可为局部等级钢筋应力，或中间等级截面内力、延性系数等，或整体等级漂移率等。

据文献［3］，EDP与IM之间服从指数回归关系:

其中:c，b为回归系数，转换到对数坐标后用最小二乘法可进行一元线性回归:

记y=ln(EDP)，x=ln(IM)，a=ln(c)

由线性回归理论，对给定x0有:

式中:t［n-2］表示自由度为(n-2)的t分布，n为样本数。其中:

1.2 概率地震需求易损性分析(PSFA)

概率地震需求模型能很好预测结构在不同强度等级地震(IM)作用下需求参数(EDP)的估计值及分布。概率地震需求模型构建后，也可解特定地震强度(IM)下工程地震需求参数(EDP)超过某值d概率P［EDP＞d| IM］，得:

式中:Tn-2［·］表示自由度为(n-2)的t分布累积概率密度函数。

1.3 概率地震需求危险性分析(PSDHA)

在概率地震需求易损性分析基础上，结合场地危险性分析结果(场地概率地震危险性函数)，可得结构对不同大小需求参数(EDP)的超越概率，即概率地震需求危险性曲线。

场地危险性函数指某场地发生不同地震动强度(IM)的超越概率。据Cornell等［7-8］研究，在感兴趣范围内场地危险性函数可表示为:

取对数后记为:

场地危险性函数可由上述理论，结合场地加速度反应谱数据由回归分析得到。

概率地震需求危险性定义:

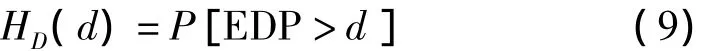
结合式(7)，得HD(d)计算方法为:

概率地震需求危险性分析，结合结构自身抗震性能分析结果与场地危险性分析结果，定量描述了结构在该场地下的危险性。

2 隔震结构与非隔震结构概率地震需求模型建立

2.1 计算模型参数

选铁路桥梁结构广泛采用的32 m简支梁桥为原型，考虑墩高为变异参数，简化为单墩模型进行计算分析。图1(a)、(b)分别为非隔震桥梁模型与铅芯橡胶支座隔震桥梁模型，墩底固接。上部结构重500 t。桥墩为实心圆端截面，为比较方便，各墩采用相同截面，尺寸见图2。桥墩采用C35混凝土;纵筋采用HRB335钢筋，直径32 mm;配箍间距100 mm，箍筋采用Q235钢筋，直径12 mm。

铅芯橡胶支座模拟采用等效双线性模型，如图3［9］所示，其中Fy为支座屈服力，Fu为支座水平极限承载力;dy为支座屈服位移，du为支座极限位移;ku为支座屈服前刚度，ku=Fy/dy，kd为支座屈服后刚度，硬化比η=kd/dy。各墩铅芯橡胶支座参数相同。计算参数见表1。

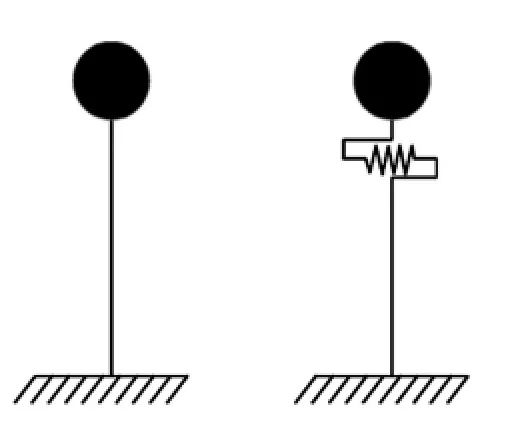
图1 计算模型示意图Fig.1 Models of the structure

图2 截面尺寸图Fig.2 Sectional dimensions

图3 支座力学性能模型Fig.3 Mechanics mode of the bearing

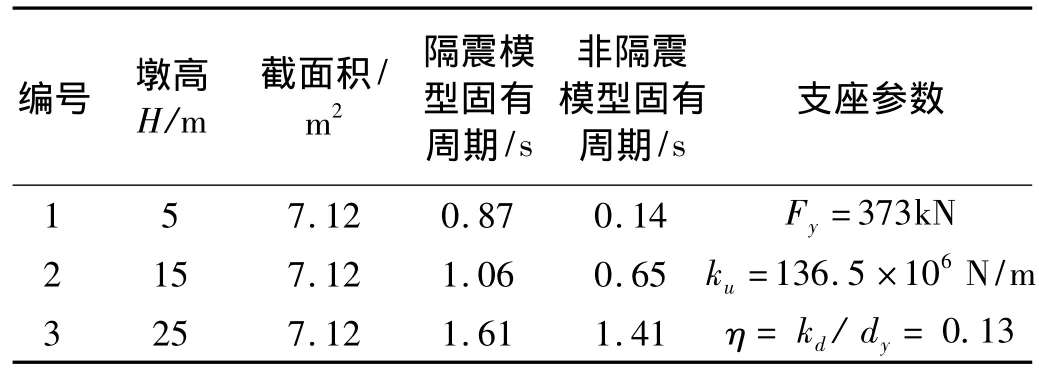
表1 模型计算参数统计Tab.1 Parameters of the models

2.2 离散地震动选取

概率地震需求分析基于选择反映该类结构所在场地的离散地震动集合，以构成‘地震动-结构’样本对，作为构建概率地震需求模型抽样。文献［3］提出用于选择地震动的‘分区法’(Ground motion bin approach)，即通过选择两个地震动特征参数，将平面划分为4个基本地震动域，在每个基本地震动域中选择合适的地震动纪录，用矩震级与震中距作为离散条件，考虑地震的普遍特性，在保证回归分析需要前提下减少所需地震动纪录数量。

本文以矩震级Mw=6.5为区分小震与大震标准，以距断层最短距离R=30 km为区分近场地震与远场地震标准［2-3］，且去除R＜15 km的地震动纪录，以排除近断层效应干扰。用‘分区法’选择40条离散的原始地震动纪录［12］，平均分布于四个区域，保证地震动纪录选择的离散性。在场地类别上，按场地剪切波速分类，含Ⅰ类、Ⅱ类场地纪录34条，Ⅲ类场地纪录6条，不含Ⅳ类场地震动纪录，以符合隔震支座适合在坚硬场地应用原则。选择地震动纪录分布见图4，选择40条地震动纪录分别与3种墩高的隔振与非隔振结构形成240个样本对。

2.3 概率地震需求模型求解

图4 地震动纪录Fig.4 The selected ground motion records

据文献［2，4］的分析与结果，本文选择Sa为IM参数，最大墩底弯矩M为EDP参数，进行概率地震需求模型构建。墩高15 m隔震结构与非隔震结构在San Fernando地震纪录为输入下，墩底弯矩响应时程见图5。墩高5 m，隔震结构周期为1.06 s，对应San Fernando地震波谱加速度值为Sa=0.16 g，时程分析得到最大墩底弯矩为M=1.19×107N·m，分别取对数后用符号‘o’标于图6(a)中;墩高15 m非隔震结构周期为0.65 s，对应San Fernando地震波谱加速度值为Sa=0.25 g，时程分析得到最大墩底弯矩为M=2.28×107N·m，分别取对数后用‘+’标于图6(b)中。

调查得知，新生信息素质教育平台目前对应的是图书馆“新生入馆教育平台”。平台内容包括本校图书馆规章制度、馆藏资源布局以及电子资源的查找利用，联机公共查询目录系统的使用方法、查找纸本、电子文献的途径及技巧等等。平台形式多样化，包括图书馆介绍视频、图书馆利用教程、新生答题系统、MOOC学习平台等。平台功能也不断扩展，可以实现网上新生培训、网上考试、实时开通借阅权限等功能。

图5 墩高15 m结构San Fernando地震纪录输入下墩底弯矩响应时程Fig.5 Pier bottom bending moment time history response of San Fernando earthquake(H=15 m)

按上述方法对2.2中抽样的40条强震纪录分别输入到各墩高隔震结构与非隔震结构中，进行非线性时程分析，计算采用SAP2000程序，并用ANSYS程序进行校核计算。对得到结果并进行回归分析。图6分别为3种墩高隔震结构和非隔震结构的样本点及回归直线。回归结果见表2。

表2 铅芯橡胶支座隔震结构与非隔震概率地震需求模型Tab.2 PSDMs of LRB isolated structures and non-isolated structures

从3种墩高铅芯橡胶支座隔震与非隔震简支桥梁模型动力时程分析结果看出，本文所得样本点(以谱加速度Sa为横坐标，最大墩底弯矩M为纵坐标，并均取对数)线性回归效果显著，表明构建的概率地震需求模型正确可靠。

隔震简支桥梁结构需求模型斜率均小于非隔震简支桥梁结构需求模型斜率，由于回归方程斜率b的意义为横坐标ln(Sa)增加一个单位时，纵坐标ln(M)的增加量。因此反映出隔震简支桥梁结构对地震动强度改变的敏感性小于非隔震简支桥梁结构;墩高增大时，隔震结构与非隔震结构需求模型斜率差距缩小，因为墩高较大的结构自身刚度小，因而隔震支座作用不明显。

对图6回归参数外的表意进一步说明:以图6(a)为例，当ln(Sa)=3.5时，两直线相交，隔震结构与非隔震结构对应的需求参数回归值ln(M)相同，但由于铅芯橡胶支座作用延长了结构自振周期(表1)，相同场地下，隔震结构遇到强度ln(Sa)=3.5的地震概率明显小于非隔震结构，如图6(a)中的非交点处。

图6 IM-EDP的回归分析Fig.6 IM-EDP regression analysis

上述3种墩高结构的回归方差均很小，但隔震结构回归方差均明显大于非隔震结构回归方差。回归方差体现了样本点相对回归方程的离散程度，由于隔震结构含有铅芯橡胶支座隔震单元，体系复杂程度提高，隔震结构响应较非隔震结构响应更离散。

3 隔震结构与非隔震结构概率地震易损性分析

地震作用下结构损害程度可分为不同等级，对应不同极限状态及EDP限值。找到这些限值，运用回归分析所得概率地震需求模型，可进一步得到桥墩概率地震易损性曲线。限于篇幅，本文仅求解桥墩中度损伤(对应桥墩墩底纵筋屈服)等级的易损性曲线，此时EDP限值为屈服弯矩My。

EDP限值与截面配筋直接相关，为对比方便，本文对3种墩高取相同配筋率:ρ=1.8%。进行弯矩-曲率分析，得到屈服弯矩My=4.97×107N·m。即EDP限值为4.97×107N·m。

由表2结果，代入式(7)计算，得到隔震结构与非隔震结构中度损伤等级下概率地震易损性曲线(ln(Sa)坐标转换为Sa坐标)，如图7所示。

由以上分析知，超越概率指发生在墩底的纵筋屈服超越概率，且对不同墩高结构采用相同截面及配筋，H=5 m隔振结构，相同梁体加速度下产生的墩底弯矩仅为H=25 m情况的1/5，表明发生墩底纵筋屈服概率在图示范围内均很小。实际中，对墩高较小结构，主要为受剪破坏，受弯破坏其次。本文目的以基于概率的方法研究支座性能，受篇幅限制，主要考察铅芯橡胶支座在减少桥墩受弯破坏的作用。

由图7知，非隔振结构均在地震强度达到某个值时出现失效概率急剧增大情况。因本文采用了简化模型，ln(M)与ln(Sa)的线性相关性显著，需求模型回归方差均很小(表2)，且非隔振结构需求模型回归方差均小于隔振结构对应值，由式(4)，当*2较小时，β值也较小，再由式(7)，结合t分布的累积概率密度曲线性质可知FR(x)曲线呈现急变的递增趋势。在极限情况下，当需求模型回归方差值为0时，ln(M)与ln(Sa)为线性关系，此时存在某一临界值，Sa小于该值时失效概率为0，Sa大于该值时失效概率为1，此极限情况下易损性曲线将呈折线形式。

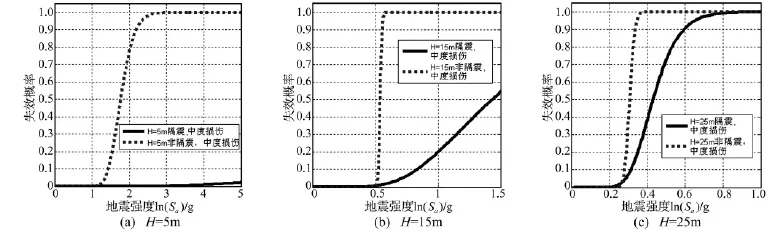
图7 概率地震易损性曲线Fig.7 Seismic demand fragility curves

从图7看到，相同谱加速度地震作用下，隔震桥梁结构失效概率远小于非隔震结构，但随墩高的增高，隔震结构优势逐渐减小。与上节分析结果一致。

4 隔震结构与非隔震结构概率地震需求危险性分析

4.1 场地危险性分析

图8 某地表加速度反应谱Fig.8 Ground acceleration response spectrum

某中硬土场地，土层等效剪切波速360 m/s，地表加速度反应谱(阻尼比0.05)如图8所示。墩高15 m的隔震结构与非隔震结构一阶自振周期分别为T=1.06 s，T=0.65 s，由加速度反应谱得:隔震结构 50 年超越概率50%，10%，2%对应的加速度反应谱值分别为 0.25 g，0.65 g，1.11 g;非隔震结构相应值为0.41 g，0.99 g，1.64 g。将该数据转换为年超越概率代入式(8)，可得该场地墩高15 m的隔震结构与非隔震结构对应的场地危险性曲线，见图9(b)。该曲线表达了不同等级地震强度及在一年内发生的超越概率。

可用同样方法得到墩高5 m，25 m的隔震结构与非隔震结构对应的场地危险性曲线，如图9(a)、图9(c)。

由图9看到，同一场地，桥梁结构体系遭遇某水平谱加速度的超越概率，隔震结构小于非隔震结构，隔震支座的应用降低了结构对应的场地危险性。且对墩高较小结构优势更明显。

4.2 概率地震需求危险性分析—铅芯橡胶支座减隔震作用总体表现

按1.3节理论，求解隔震结构与非隔震结构的概率地震需求危险性曲线，见图10。此为墩底弯矩-年超越概率曲线。

图9 场地危险性曲线Fig.9 Site hazard curves

由图10看到，在该场地条件下，墩高5 m，15 m，25 m非隔震结构发生墩底纵筋屈服的年超越概率分别为6.49 ×10-4，7.53 ×10-3，5.82 ×10-3;墩高 5 m，15 m，25 m隔震结构对应的年超越概率分别为2.45×10-6，4.22 ×10-4，2.23 ×10-3。

芯橡胶支座的隔震作用，表现在两方面:① 改善了桥梁结构的耗能机制;② 减少了地震动输入到桥梁结构的能量。不同等级墩底弯矩的年超越概率是铅芯橡胶支座的隔震性能总体表现。由图10看出，铅芯橡胶隔震支座的应用，明显减小了桥梁结构发生损害的年超越概率，且墩高越小，作用越明显。对实际工程，墩高一旦确定，即可对用不同参数的隔震支座桥梁进行计算。用本文方法定量比较墩底屈服年超越概率，从而选择最优参数的隔震支座。

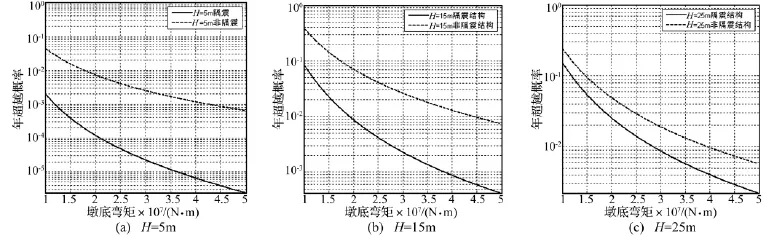
图10 概率地震需求危险性曲线Fig.10 Probabilistic seismic demand hazard curves

概率地震需求危险性曲线(图10)较结构易损性曲线(图8)优势明显:① 需求危险性曲线综合了易损性分析及场地危险性分析所得结果(式(10))，表达某结构在特定场地的危险性;而图8中结构易损性曲线仅表现结构自身抗震特性，与所处场地无关，故需求危险性曲线较易损性曲线工程应用价值更大。② 需求危险性曲线表现不同数值墩底弯矩的年超越概率，对较大墩底弯矩其对应的年超越概率相应较小，曲线呈逐渐下降的、趋势;而图8中结构易损性曲线表达为对某一特定墩底弯矩值，随地震强度的增大，墩底弯矩响应超过该值的概率也增大，曲线呈急变递增趋势，因此，需求危险性曲线的表达方式更符合工程技术人员习惯。

5 结论

综合以上计算及分析，结论如下:

(1)本文通过地震动分区法，保证了输入地震动的离散性，由谱加速度Sa与最大墩底弯矩M构成的样本点回归方差小，建立的概率地震需求模型结果正确可靠。

(2)概率地震需求模型计算结果表明，铅芯橡胶隔震支座隔震桥梁结构需求模型斜率均小于非隔震结构对应斜率，反映出隔震结构对地震动强度改变的敏感性小于非隔震结构。

(3)场地危险性分析表明，同一场地桥梁结构体系遭遇某水平谱加速度的超越概率，隔震结构小于非隔震结构，隔震支座的应用降低了结构对应的场地危险性。

(4)不同墩底弯矩的年超越概率(概率地震需求危险性曲线)是铅芯橡胶支座减隔震性能的总体表现，在本文设定的场地及结构下，隔震桥梁结构发生墩底纵筋屈服年超越概率远小于非隔震结构相应概率。且墩高越低，隔震作用越明显。

(5)概率地震需求分析方法作为基于概率的定量分析方法，可应用于不同结构体系桥梁结构抗震性能的评价。

［1］Porter K A.An overview of PEER’s performance-based earthquake engineering methodology［C］.Proceedings of the 9th International Conference on Applications of Statistics and Probability(ICASP9)in Civil Engineering，2003，2:973-980.

［2］Kevin M，Bozidar S，Seismic demands for performance-based design of bridges［R］.Pacific Earthquake Engineering Research Center，University of California，Berkeley，2003.

［3］Shome N.Probabilistic seismic demand analysis of nonlinear structures［D］.PhD Dissertation:Stanford University，1999.

［4］Kevin M，Bozidar S，Probabilistic seismic demand model for california highway bridges［J］. Journal of Bridge Engineering，ASCE，2001，6(6):468-481.

［5］Nielson B G，DesRoches R.Seismic fragility methodology for highway bridges［C］.Proceedings of the 2006 Structures Congress，2006.

［6］Zhang Y Y.Probabilistic structure seismic performance assessment methodology and application to an actual bridgefoundation-ground system［D］.PhD Dissertation:University of California，San Diego，2006.

［7］ Cornell C A.Engineering seismic risk analysis［J］.Bulletin of the Seismological Society of America，1968，58(5):1583-1606.

［8］ Cornell C A， Jalayer F，Hamburger R O， et al. A probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines ［J］.Journal of Structural Engineering，ASCE，2002，124(4):526-533.

［9］钟铁毅，杨风利，吴 彬.铅芯橡胶支座隔震铁路简支梁桥双向地震响应分析［J］.中国铁道科学，2007，28(3):38-43.

ZHONG Tie-yi，YANG Feng-li，WU Bin.Analysis of the bidirectional seismic response for seismically isolated railway simple supported beam bridge by lead rubber bearing［J］.China Railway Science，2007，28(3):38-43.

［10］陈 亮，李建中，管仲国，等.强地面运动持时对钢筋混凝土桥墩地震需求的影响［J］.振动与冲击，2008，27(11):154-159.

CHEN Liang，LI Jian-zhong，GUAN Zhong-guo，et al.Influence of strong-motion duration on seismic inelastic demand for columns of RC bridges［J］.Journal of Vibartion and Shock，2008，27(11):154-159.

［11］吕大刚，于晓辉，潘 峰，等.基于改进云图法的结构概率地震需求分析［J］.世界地震工程，2010，26(1):7-15.

LÜ Da-gang，YU xiao-hui，PAN Feng，et al.Probabilistic seismic demand analysis of structures based on an improved cloud method ［J］.World Earthquake Engineering，2010，26(1):7-15.

［12］ Peer strong ground motion database［C］.http://peer.berkeley.edu/peer_ground_motion_database/.