连续梁桥墩底自复位减隔震机理及参数优化分析
2018-09-28张文学赵汗青
张文学, 赵汗青, 赵 旭, 张 红
(1. 北京工业大学 建筑工程学院, 北京 100124;2. 北京工业大学 城市与工程安全减灾省部共建教育部重点实验室, 北京 100124)
连续梁桥具有整体刚度大、行车平顺、维护费用较低等优点,在我国铁路工程中广泛应用。然而连续梁桥一般每联只设一个固定墩,其他各墩均为活动墩。在纵向地震作用下,上部结构的地震作用几乎全部由单个固定墩承担,这使得固定墩的能力往往难以满足抗震需求。虽然通过在桥墩指定位置设置塑性铰,使桥墩在罕遇地震情况下发生塑性变形,可以降低结构的整体地震响应[1],但由于铁路桥墩截面较大,配筋率较低,很难实现塑性铰设计。其次,即便通过精心设计,在强震作用下固定墩在指定位置形成了塑性铰,避免结构倒塌震害的发生,但因残余变形过大及主要承重构件破损严重等原因,致使灾后修复极为困难,甚至不得不拆除重建[1]。为此有学者提出通过支座实现减隔震的抗震设计思想,在墩顶安装减隔震支座隔绝地震能量向上部结构的传递。目前在实际工程中使用较多的减隔震支座有铅芯橡胶支座、摩擦摆支座、高效阻尼型支座和牵拉限位支座等[1]。杨喜文等[2]研究认为摩擦支座并联阻尼器或双曲面球型减隔震支座均可减小固定墩的地震响应。袁万城等[3-4]提出的拉索减震支座,在理论研究与多种结构形式的桥梁实验中均表现出较好的减震效果。黎雅乐等[5]设计了1个1∶3的连续梁桥振动台模型,进行了强震作用下连续梁桥地震响应实验,研究表明采用高阻尼橡胶支座可以有效控制边墩的地震响应,降低落梁风险。Kataria等[6]在连续弯桥上将半主动变刚度阻尼器与铅芯橡胶支座组合使用,并取得了很好的减震效果。Alam等[7]和Hedayati等[8]分别对不同支座安装形状记忆合金限位器后的地震响应进行研究,结果表明:形状记忆合金限位器的存在能显著减小板式橡胶支座的失效概率,增加高阻尼橡胶支座的侧向刚度,并具备自动复位的功能。Lu等[9]结合静力实验发现选择适当的参数后的摇摆支座能有效的减小近断层地震引起的支座位移。综上所述,在墩顶安装减隔震支座可以阻止地震能量传递到连续梁桥的上部结构,在一定程度上降低结构的地震响应,但仍不能减小桥墩自身引起的地震响应,特别是对于超高墩不能有效保证桥墩在地震作用下不会发生损伤。
近些年有学者提出基底减隔震技术,即将墩底和承台之间采用分离式设计,同时在分离界面附近安装一些耗能装置[10]。Jonsson等[11]依托冰岛某座370 m震损桥梁,提出基底隔震代替原有的铅芯橡胶支座的改进设计。Lolil等[12]实验后发现,地基土具有一定的能量耗散机制,摇摆桥墩具有显著的隔震效果。王军文等[13]根据基于性能抗震设计的思想,提出一种摇摆式预应力混凝土桥墩的抗震设计方法。杨浩林[14]将传统桥梁桩基础的承台一分为二,使承台上部能够在地震作用下摇摆,从而在基础部位隔断地震传播途径,达到减隔震的目的。夏修身等[15-16]对墩底隔震技术进行了较为系统的研究,先后提出了墩底隔震简化计算的两弹簧模型和考虑限位装置的三弹簧模型,研究表明采用墩底摇摆隔震技术具有较好的隔震效果,可以实现墩底最大弯矩不受地震输入特性的影响,且可以同时保护桥墩和基础。但进一步的研究表明采,用平面接触的基地摇摆隔震技术的减隔震效果受近场竖向地震作用和提离弹簧刚度等参数影响明显[17-19]。
虽然已有的研究表明采用墩底减隔震技术具有很好的减隔震效果,但目前研究多采用平面或球形接触面的基底减隔震结构。进一步深入研究发现采用平面接触基底减隔震结构时,结构的地震响应是不连续的,存在明显的“反磕”现象,甚至会因此增大结构的地震响应。而采用球形接触面的基底减隔震结构,虽然结构的地震响应是连续的,也可以有效降低结构的内力响应,但结构的位移响应过大,且不具备自复位功能,震后残余变形过大。为此,从铁路连续梁桥的结构形式及特点出发,提出一种新型自复位墩底减隔震结构,在正常使用情况下该结构具有一定的稳定刚度,可以满足安全行车需求;在强震作用下,固定墩墩底与承台之间发生相对往复摇摆,不仅起到隔震效果,而且可以通过往复摩擦摇摆消耗部分地震能量;更重要的是该墩底减隔震结构具有震后自复位功能,便于震后修复与加固。以典型铁路三跨连续梁桥为例,建立非线性有限元模型,系统研究了墩底自复位减隔震结构的减隔震机理及其主要结构参数对减隔震效果的影响。
1 连续梁桥固定墩墩底自复位减隔震结构
1.1 墩底自复位减隔震结构设计
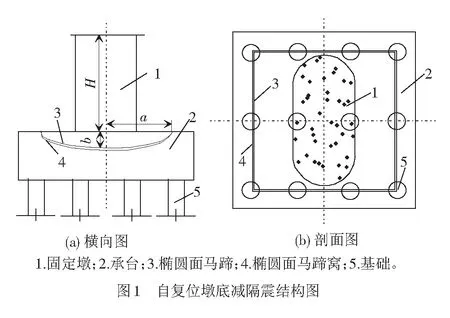
墩底自复位减隔震结构由固定墩、承台、椭圆面马蹄、椭圆面马蹄窝和基础组成,见图1。桥墩底部的椭圆面马蹄与承台上方的椭圆面马蹄窝处于隔离状态。在正常使用情况下,桥墩可在竖向自重作用下与承台之间保持相对固定以满足正常使用需求。地震突发时,固定墩底的马蹄与承台马蹄窝之间发生相对滑移和摆动,整个连续梁桥的上部结构和固定墩一起绕马蹄窝做往复摆动,不仅起到隔震效果,还可利用固定墩墩底马蹄与承台马蹄窝之间摩擦滑移而耗散部分地震能量,起到减震效果,进而降低固定墩的地震需求,提高连续梁桥的整体抗震性能。地震动峰值过后,在结构自重和地震余能的共同作用下,上部结构和固定墩均能自动恢复到初始平衡位置,有利于震后及时通车和灾后维修加固。
1.2 墩底自复位减隔震结构的减隔震效果
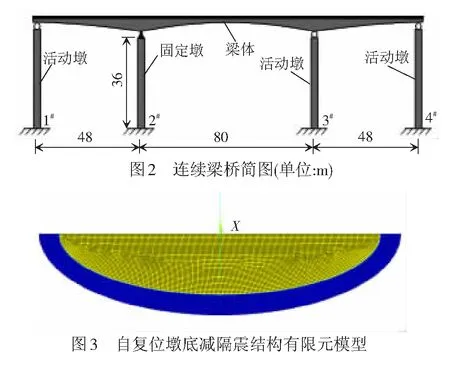
为验证墩底自复位减隔震结构的减隔震效果,以客运专线(48+80+48)m标准连续梁桥为例进行了减隔震分析,见图2。连续梁的混凝土标号为C50,混凝土弹性模量Eb=3.45×1010N/m2,总重量W=73 138 kN;桥墩混凝土标号为C30,混凝土弹性模量Ep=3.00×1010N/m2,取墩高H=36 m,各桥墩的纵向抗弯惯性矩I=118.54 m4。采用ANSYS软件分别建立2种分析模型,模型1为常规连续梁桥模型(暂不考虑地震作用下的塑性变形),模型中1#、3#、4#墩为活动墩,2#墩为固定墩,4个桥墩墩底均简化为固结。模型2为墩底自复位减隔震模型,模型中1#、3#、4#墩为活动墩,墩底简化为固结,2#固定墩墩底采用自复位减隔震结构。模型1和模型2均不考虑桩土相互作用。模型中连续梁和桥墩均采用线性梁单元BEAM3模拟。模型2的墩底自复位减隔震结构采用2D面单元PLANE82模拟,马蹄与马蹄窝间非线性摩擦接触采用CONTA172接触单元和TARGE169目标单元模拟,接触摩擦系数μ=0.3,马蹄和马蹄窝的椭圆长半径a=4 m,短半径b=1.5 m,桥梁结构的阻尼比c=5%。墩底自复位减隔震结构局部模型见图3。
为方便分析墩底自复位减隔震结构对连续梁桥的减隔震效果,定义墩底剪力、墩底弯矩的减震率λ和梁端纵向位移放大倍数γ为
( 1 )
( 2 )
式中:R1为模型1所得结构最大地震响应;R2为模型2所得结构最大地震响应。
选取Ⅰ类场地广州波、Ⅱ类场地El-Centro波、Ⅲ类场地兰州波和Ⅳ类场地天津波为地震动输入,且所有地震波的加速度峰值均为0.4g,计算结果见表1。4种不同场地类型的纵向输入地震波频谱特性见图4。在El-Centro波作用下的地震响应时程曲线见图5。
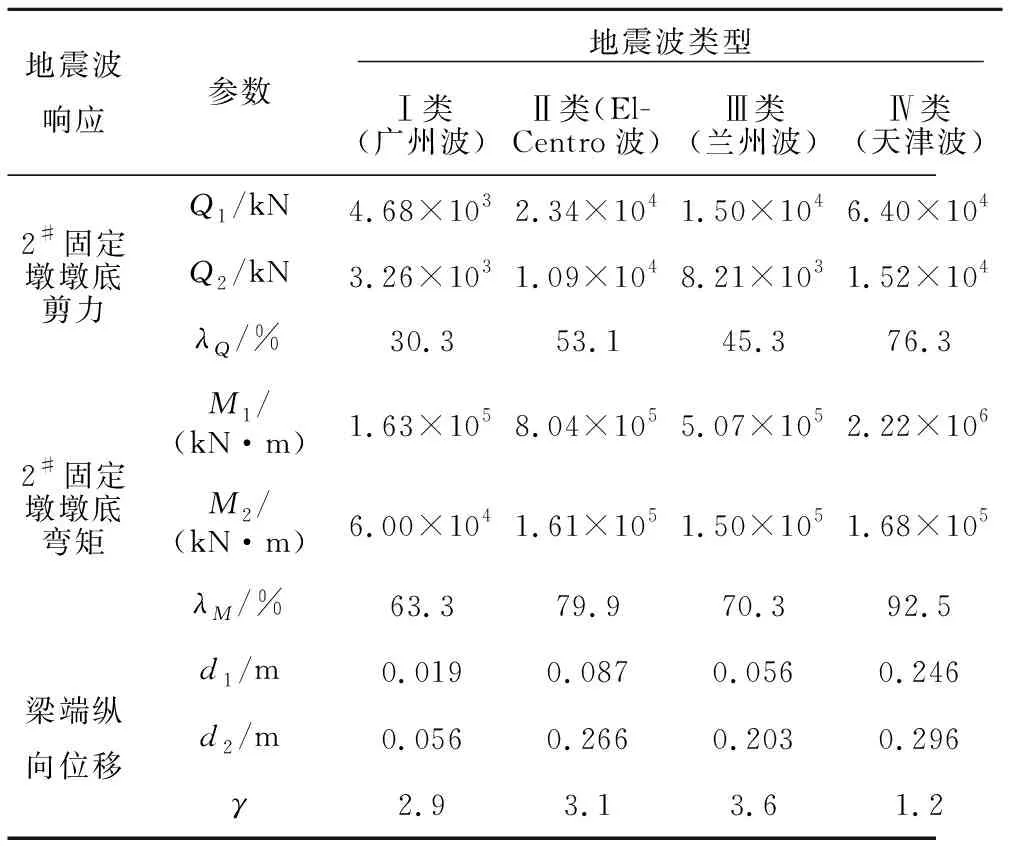
表1 减隔震效果
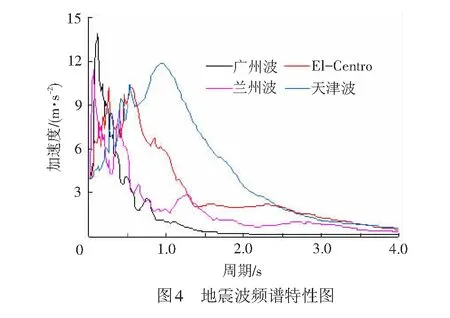
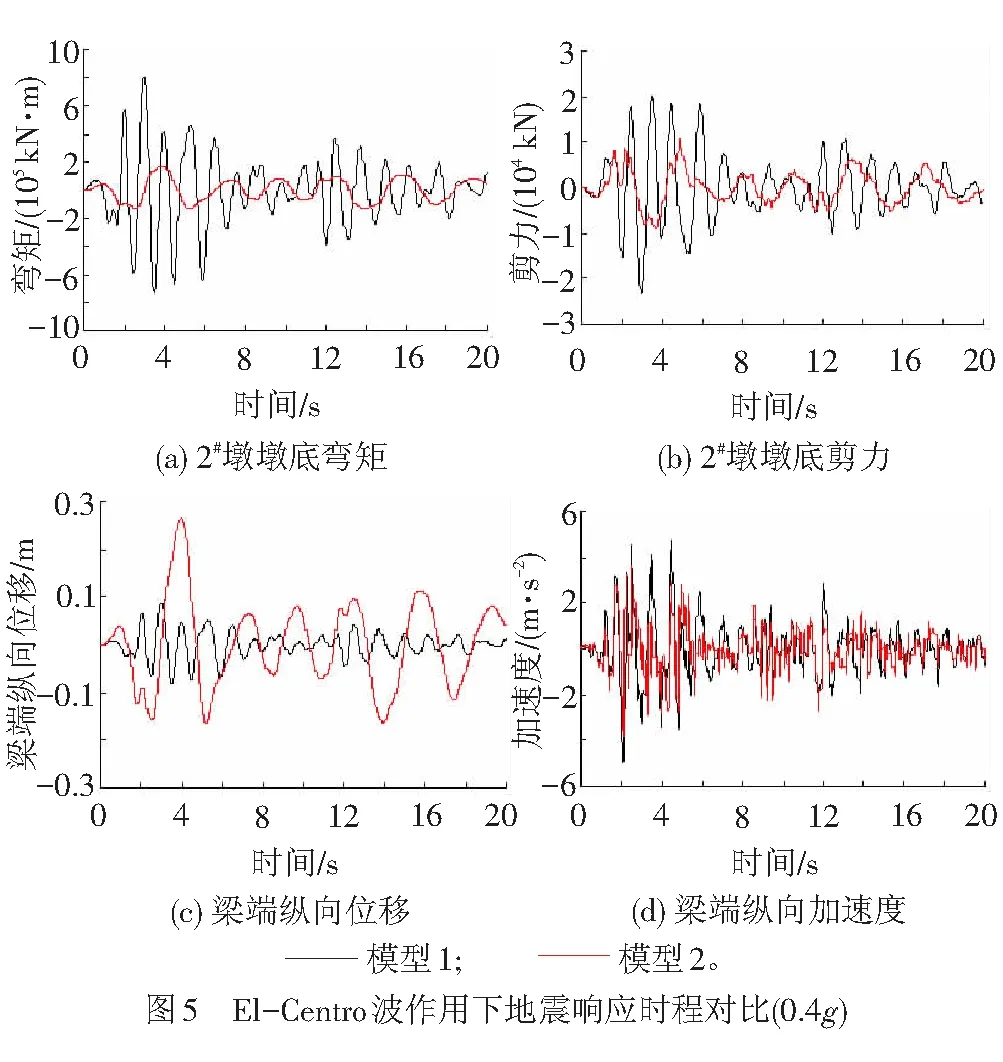
由表1和图4、图5可知:
(1) 墩底设置自复位减隔震结构对连续梁桥固定墩墩底的剪力和弯矩响应均有非常明显的减隔震效果,在给定地震波作用下墩底剪力响应的减震率为30.3%~76.3%,墩底弯矩响应的减震率为63.3%~92.5%。具体减隔震效果受场地类型影响比较明显,在本文采用的4种不同场地类型地震波作用下,固定墩墩底剪力响应的减震率相差40%以上,墩底弯矩响应的减震率相差约29%;在Ⅰ类场地地震波作用下的减隔震效果不如Ⅱ~Ⅳ类型场地地震波作用下的减隔震效果好;在相同类型场地条件下固定墩墩底弯矩的减隔震效果明显优于墩底剪力响应的减隔震效果。
(2) 墩底自复位减隔震结构在有效降低固定墩地震内力需求的同时也增大了梁端的纵向位移响应,在表1给出的4种不同场地类型地震波作用下,梁端纵向位移的放大倍数在1.2~3.6间。本文分析模型采用墩底自复位减隔震结构后,在最大加速度峰值0.4g的地震波作用下梁端的最大位移为0.296 m,仍小于本算例桥梁伸缩缝允许的伸缩范围,但在实际应用中应予以重视。
(3) 固定墩墩底设置自复位减隔震结构后,固定墩的剪力、弯矩和梁端纵向位移响应的周期明显增大,增大幅度在2.5倍以上。
1.3 墩底自复位减隔震结构的减隔震机理
为了进一步研究墩底自复位减隔震结构的减隔震机理,以El-Centro波和天津波为地震输入,研究不同地震加速度峰值(PGA=0.05g、0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g)作用下,各个分析模型2#固定墩墩底内力的变化规律,见图6、图7。其中,模型1-1为不考虑墩底塑性铰的常规结构对照模型;模型1-2为考虑墩底塑性铰的常规结构对照模型,即在2#固定墩墩底建立塑性铰单元,其M-φ曲线通过UCFyber程序求得,等效屈服弯矩Me=7.26×105kN·m;模型2为墩底自复位减隔震模型。在图7中,Mmax为设置墩底自复位减隔震结构后2#固定墩墩底的理论最大弯矩响应,Mmax=N·a=2.27×105kN·m(N为静力分析下2#固定墩的墩底支反力,a为墩底马蹄的长轴半径)。天津波作用下地震响应时程与地震加速度峰值的关系见图8,固定墩墩底内力的减震率与地震加速度峰值的关系见图9。

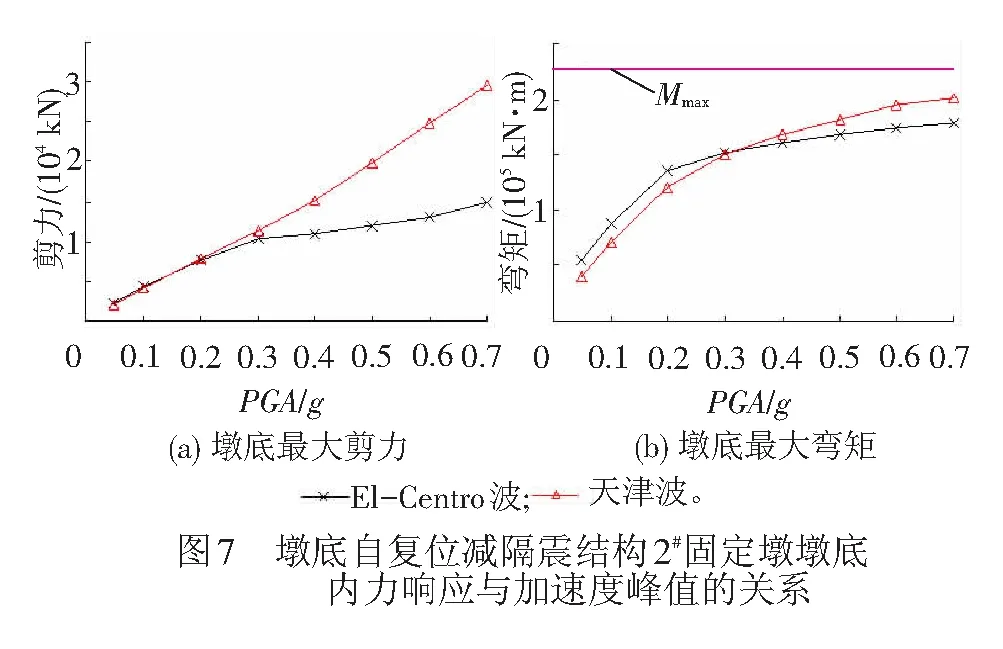
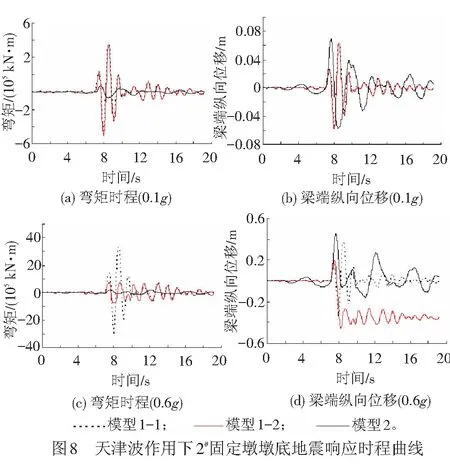

由图6~图9可知:
(1) 模型1-1在两种地震波作用下,固定墩墩底地震内力响应随着加速度峰值的增大而增大,呈现出线性变化规律。模型1-2在两种地震波作用下,固定墩墩底地震内力响应随着加速度峰值的增大而增大,呈现出两线性变化规律。此外,在天津波(0.1g)和El-Centro波(0.3g)时,模型1-2开始出现塑性铰,进入塑性阶段,并在天津波(0.2g)和El-Centro波(0.5g)时达到等效屈服弯矩Me。在模型1-2墩底发生塑性变形之前,模型1-1和模型1-2的2#固定墩墩底内力响应随地震加速度峰值增加而增大的规律基本一致,墩底弯矩响应和剪力响应均随加速度峰值的增加而线性增加。当固定墩的墩底弯矩响应达到等效屈服弯矩Me时,即模型1-2墩底出现塑性铰后,固定墩墩底的弯矩响应几乎不再随PGA的增加而增大,而固定墩墩底的剪力响应随PGA的增加而略有增大,但增大速率明显减小。
(2) 设置墩底自复位减隔震结构后的模型2,在两种地震波作用下,固定墩墩底地震弯矩响应随着地震动加速度峰值的增大而增大,且呈现出两阶段线性变化规律,第一阶段为地震加速度峰值小于0.2g时,固定墩墩底弯矩响应随地震加速度峰值增大而增大的速率较快(斜率较大);地震加速度峰值大于0.2g后,进入第二阶段,此时固定墩墩底弯矩响应随地震加速度峰值增大而增大的速率明显下降,墩底最大弯矩始终小于理论计算值Mmax。虽然模型2固定墩墩底最大剪力响应仍随地震加速度峰值的增加而有所增大,但增加幅度明显小于模型1-1和模型1-2,仍具有很好的减隔震效果。在采用本文提出的墩底自复位减隔震结构进行连续梁桥减隔震设计时,建议取理论最大弯矩Mmax小于固定墩的等效屈服弯矩Me,进而确保在强震作用下固定墩不发生严重破坏,以便灾后修复。
(3) 按常规连续梁桥进行抗震设计,在强震作用下固定墩墩底形成塑性铰,可以有效控制固定墩的内力响应,弯矩和剪力均呈现出两阶段线性变化的规律,但结构位移响应因塑性铰而偏离了初始平衡位置,震后残余变形较大,不利于灾后及时通车和修复。
(4) 采用本文提出的墩底自复位减隔震结构后,在强震作用下不仅对固定墩内力响应具有很好的减震效果,而且震后残余变形小,具有较好的自复位功能。
2 墩底自复位减隔震结构参数分析
2.1 摩擦系数μ的影响
摩擦系数μ的取值大小对墩底自复位减隔震结构的减隔震效果有一定影响,不仅决定固定墩墩底的椭圆面马蹄何时开始与椭圆面马蹄窝相对滑动,起到隔震作用,而且影响相对滑移时消耗地震能量的多少。因此有必要分析μ对减隔震效果的影响。以上述三跨等高连续梁桥为例,地震波选择El-Centro波和天津波,加速度峰值均为0.4g,墩高H=36 m,椭圆长半径a=4 m,短半径b=1.5 m,马蹄与马蹄窝之间的μ分别取为0.15、0.20、0.25、0.30、0.35,分析μ对墩底自复位减隔震结构减隔震效果的影响,分析结果见图10,由图10可知:
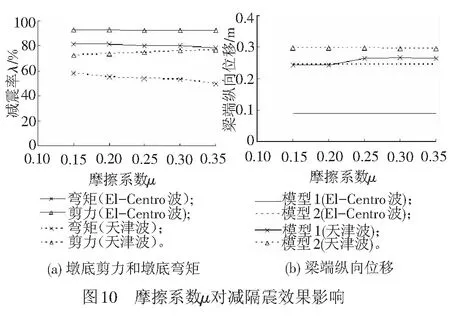
(1) 摩擦系数对墩底自复位减隔震结构的减隔震效果有一定影响,但影响幅度非常小。在El-Centro波和天津波作用下,随摩擦系数的增大,墩底弯矩的减震率均略有降低。在El-Centro波作用下墩底剪力的减震率随摩擦系数的增大而有所减小,在天津波作用下墩底剪力的减震率随摩擦系数的增大反而有所增大。
(2) 摩擦系数对采用墩底减隔震结构连续梁桥的梁端纵向位移响应的影响很小,且不具有规律性,当摩擦系数μ在0.15 ~ 0.35间时,采用墩底自复位减隔震结构后的梁端纵向位移响应均大于传统连续梁桥的梁端纵向位移响应。
(3) 当摩擦系数μ的取值范围为0.15 ~ 0.35时,墩底自复位减隔震结构对固定墩墩底弯矩响应的减震率均大于75%,对固定墩墩底剪力响应的减震率均大于50%;说明本文提出的墩底自复位减隔震结构不仅具有较好的减隔震效果,而且对结构摩擦系数的适应性较好。
2.2 长半径a的影响
墩底自复位减隔震结构椭圆面长半径a会直接影响其减隔震效果和自复位能力。因此,有必要研究椭圆面长半径a对减隔震效果的影响。仍采用上述三跨等高连续梁桥,地震波选择El-Centro波和天津波,加速度峰值均为0.4g,保持墩高H=36 m、短半径b=1.5 m和摩擦系数μ=0.30不变,分别取长半径a为2、3、4、5、6 m(桥墩厚度B=4 m,承台顺桥向尺寸一般为12~15 m),分析长半径a对自复位墩底减隔震结构减隔震效果的影响,分析结果见图11。

由此可知,在减隔震结构椭圆短半径b、摩擦系数μ和桥墩高度H一定的情况下,减隔震结构椭圆长半径a对固定墩墩底弯矩和剪力的减震率有一定影响,墩底弯矩减震率随长半径a的增大略有降低,但对墩底剪力减震率的影响不具规律性。自复位减隔震结构椭圆长半径a对连续梁桥梁端纵向位移响应有一定影响,但其影响不具明显规律性。对本算例中的连续梁桥,当长半径a的取值范围为2~6 m时,墩底自复位减隔震结构对固定墩墩弯矩响应的减震率均大于70%,对固定墩墩底剪力响应的减震率均大于45%。
2.3 短半径b的影响
采用上节分析模型,地震波为El-Centro波和天津波,加速度峰值均为0.4g,墩高H=36 m,长半径a=4 m,摩擦系数μ=0.30,取减隔震结构短半径b为1.0、1.5、2.0、3.0、4.0 m(当b=4.0 m=a,接触面为圆形),分析短半径b对墩底自复位减隔震结构减隔震效果的影响,分析结果见图12、图13。
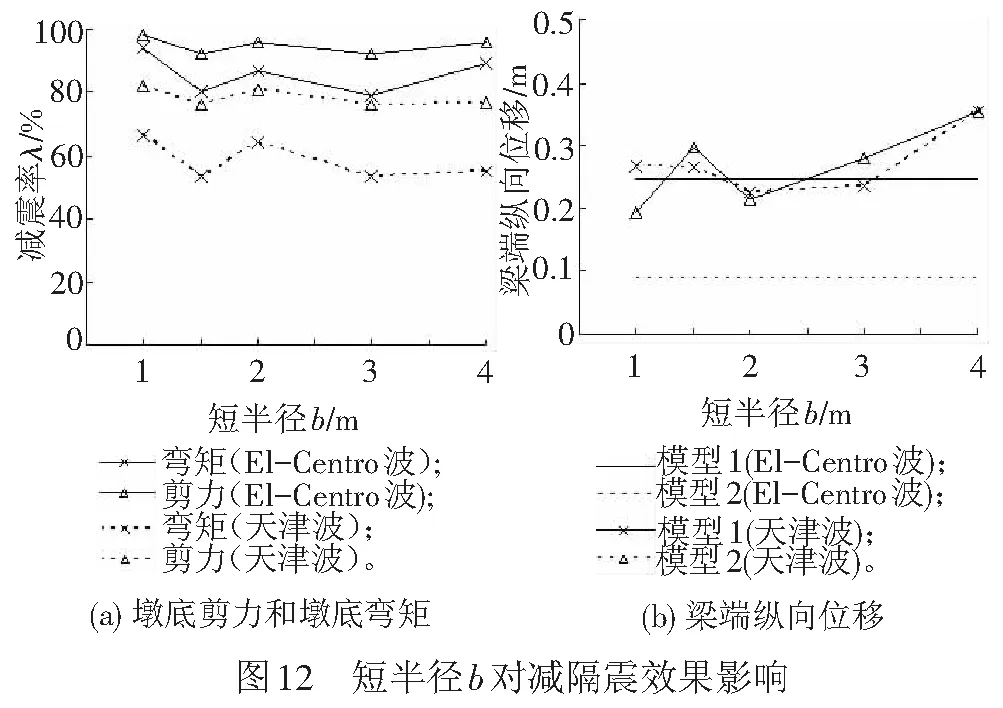
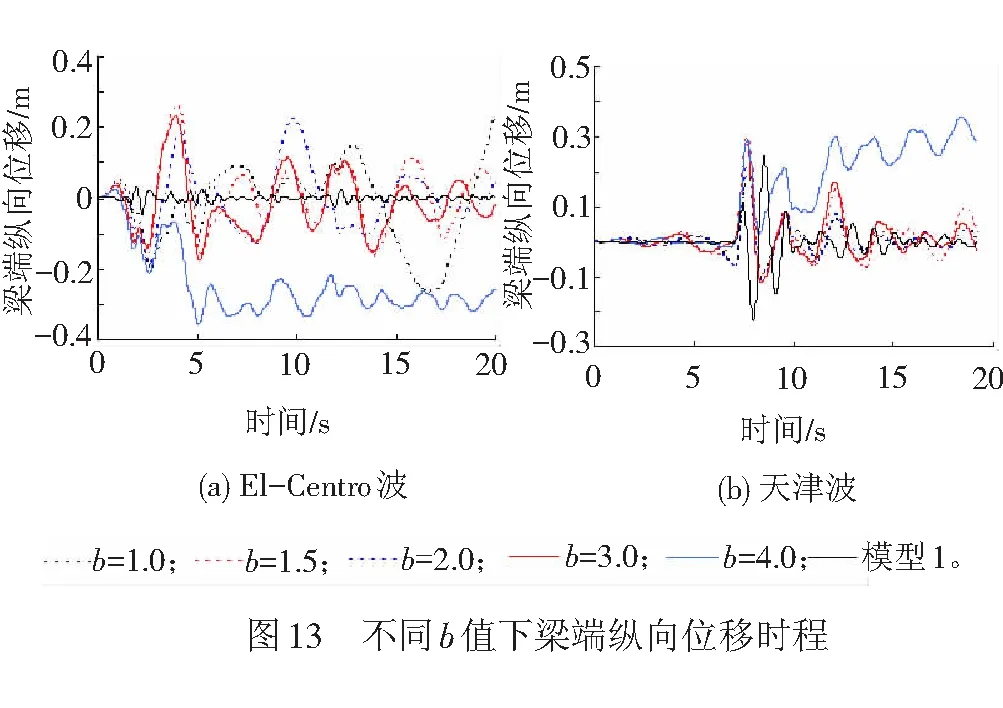
由图12和图13可知:
(1) 当长半径a、摩擦系数μ和墩高H不变时,短半径b的取值对固定墩墩底弯矩和剪力的减震率均有较大影响。短半径b取值在0.25a~1.00a范围时,固定墩墩底弯矩和剪力的减震率均呈现出无明显规律的波动趋势。
(2) 当长半径a、摩擦系数μ和墩高H不变时,短半径b的取值对采用墩底自复位减隔震结构后连续梁桥梁端纵向位移响应有较大影响。当短半径b取值在0.25a~0.50a范围时,梁端纵向位移响应呈现出无明显规律的波动趋势;当短半径b取值在0.50a~1.00a范围时,梁端纵向位移响应随短半径b取值的增大而增大。
(3) 当短半径b与长半径a相等时,在地震过程中上部结构偏离原位置而振动,不仅梁端纵向位移响应较大,而且震后结构不能回到原位置,结构纵向残余变形较大,不具备震后自复位能力。此时虽然具有很好的减隔震效果,但对桥梁伸缩缝和滑动支座不利,不利于灾后修复。
(4) 考虑到对固定墩内力响应减震率和对梁端纵向位移响应的影响及震后残余变形的控制,建议取墩底自复位减隔震结构短半径b取值范围为a/3~a/2比较合理。
2.4 墩高H的影响
仍采用上述三跨等高墩连续梁桥为分析对象,地震波选择El-Centro波和天津波,取减隔震结构的长半径a=4.0 m、短半径b=1.5 m、摩擦系数μ=0.30,墩高H分别取24、36、48、60 m,分析墩高对墩底自复位减隔震结构减隔震效果的影响,分析结果见图14,由图14可知:
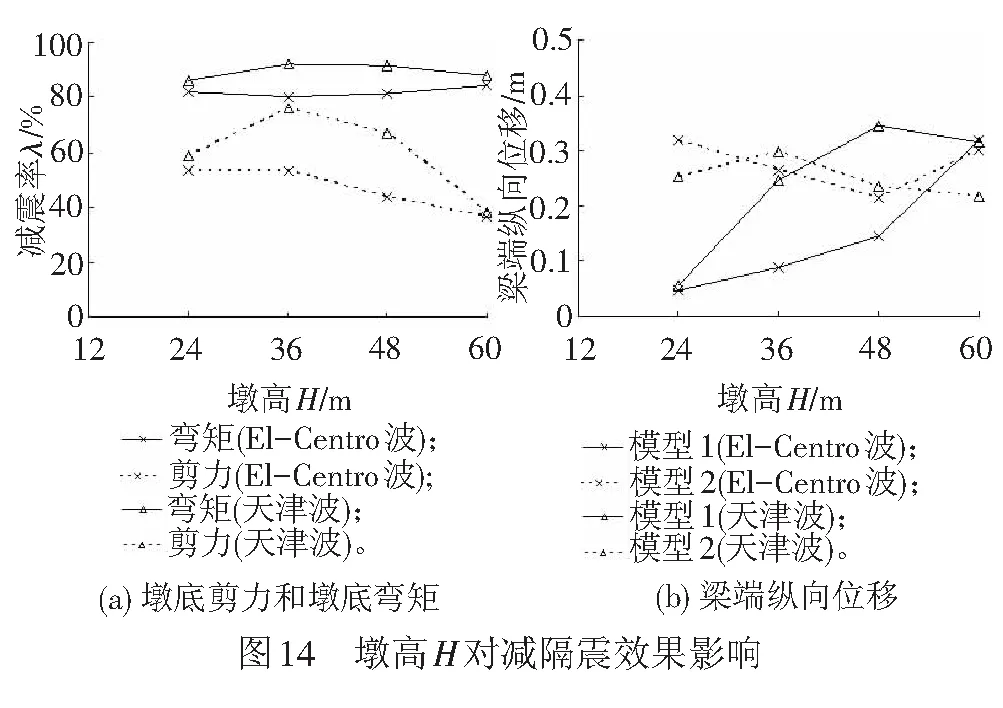
(1) 在减隔震结构的长半径a、短半径b和摩擦系数μ不变的情况下,墩高H对固定墩墩底弯矩的减震效果影响很小,但对墩底剪力的减震效果影响较大,当墩高H较大时固定墩墩底剪力的减震率明显降低。
(2) 在减隔震结构的长半径a、短半径b和摩擦系数μ不变的情况下,墩高H对梁端纵向位移响应有较大影响,随着墩高H的增大,采用墩底自复位减隔震结构后梁端纵向位移响应放大倍数γ随之有所降低,甚至会出现采用墩底自复位减隔震结构后,梁端纵向位移响应低于传统连续梁桥的情况。说明对于桥墩较高的连续梁桥,采用本文提出的墩底自复位减隔震结构后不一定增加梁端的纵向位移需求。
3 自复位结构长短半径比a/b对滞回性能影响分析
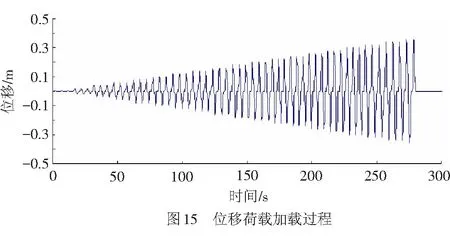
为进一步研究墩底自复位减隔震结构的滞回性能,采用控制位移逐步循环加载方法,以上述的3跨等高墩连续梁桥为原型,研究了墩底自复位减隔震结构长短半径比a/b对其滞回性能的影响规律。位移荷载初始值为0 m,最大纵向位移值为0.4 m,每级荷载值循环加载3次。具体加载过程见图15。共建立6组不同长短半径比墩底减隔震模型,取摩擦系数μ=0.30、长半径a=4 m,长短半径比a/b的取值为1~6。分析得出的墩底自复位减隔震结构的滞回曲线见图16,由图16可知:
(1) 当墩底减隔震结构的长短半径比a/b=1时,即接触面为常规圆形,此时减隔震结构的滞回曲线非常饱满,且具有很好的耗能性能,但其不具备自复位功能,不是理想的减隔震结构。
(2) 随着墩底减隔震结构长短半径比a/b的增加,减隔震结构的滞回曲线迅速收窄。当a/b=2,且位移较小时,滞回曲线接近于直线型,残余变形非常小;随着位移幅度的增大,滞回曲线越来越饱满,呈现出“鸟翼”型,两端饱满,中间收窄,不仅具有较好的耗能能力,而且残余变形小,表现出较好的自复位功能。当a/b=3时,墩底减隔震结构的滞回曲线进一步收窄,两头尖,中间稍宽,呈S型,虽残余变形越来越小,自复位功能越来越好,但耗能性能迅速降低。随着长短半径比a/b的进一步增加,墩底减隔震结构的滞回曲线越来越窄,由S型过渡到近似直线型,虽然自复位功能越来越好,但耗能性能迅速消失。
(3) 综合分析,建议取墩底减隔震结构的长短半径比a/b=2~3比较合理,不仅具有较好的耗能性能,而且具有很好的自复位功能。在实际的抗震设计中,应分析墩底自复位减隔震结构的长短半径比a/b对其滞回性能的影响,确定出最优长短半径比a/b,使得墩底自复位减隔震结构具有较好的耗能性能和自复位功能。
4 结论
针对强震区铁路连续梁桥固定墩内力响应过大,常规减隔震措施难以满足抗震需求这一问题,提出在连续梁桥固定墩墩底设置椭圆形自复位减隔震结构来降低固定墩的地震需求。以一典型铁路连续梁桥为例,建立减隔震结构非线性分析模型,研究了自复位减隔震结构的减隔震效果和减隔震机理,分析了结构参数对墩底自复位减隔震结构减隔震效果的影响,得出如下主要结论:
(1) 本文提出的连续梁桥墩底自复位减隔震结构不仅具有较好的减隔震效果,而且具有较好的自复位功能,有利于灾后修复加固。
(2) 在固定墩出现塑性铰之前,墩底自复位减隔震结构的减隔震效果随地震加速度峰值的增加而增大;在相同情况下,墩底自复位减隔震结构对固定墩墩底弯矩响应的减震率明显优于对墩底剪力响应的减震率。采用本文提出的墩底自复位减隔震结构时,为确保固定墩不发生破坏,建议取固定墩墩底的最大理论弯矩Mmax=Na小于固定墩的等效屈服弯矩Me。
(3) 墩底自复位减隔震结构的长半径a、短半径b及连续梁墩高H对减隔震效果影响较大,而摩擦系数μ对其减隔震效果影响很小,可以忽略。
(4) 墩底减隔震结构的长短半径比a/b对其滞回性能有较大影响,当a/b=1时减隔震结构的耗能性能最好,但不具备自复位功能;随着a/b的增加,减隔震结构的自复位性能迅速增加,但耗能性能迅速降低。
(5) 综合考虑固定墩内力响应减震率、梁端纵向位移响应及震后残余位移等因素,取墩底自复位减隔震结构的长短半径比a/b=2~3比较合理。
