基于小波变换的图像水印技术

邓文权，廖述剑

(太原理工大学 信息工程学院，山西 太原030024)

随着现代科技的飞速发展，人们日益频繁地接触到各种各样的数字化产品。在开放的网络环境下也滋生出一系列的关于版权保护的问题。当今时代，盗版者轻易就可得到与原版相同的复制品，某些重要的机密，如涉及司法诉讼、政府机要等信息也会遭到恶意攻击和篡改伪造。数字水印是一种非常有效的信息安全技术，相对于其他的版权保护系统，数字水印技术有着先天的巨大优势，只需要稍稍一点失真度就可以把数字水印永久地嵌入到多媒体数据中。受版权保护图像中嵌入水印信息，水印检测过程中，通过密钥提取水印并检测图像的所有版权，对版权信息进行确认。在出现版权纠纷时，作品所有者利用从盗版作品中提取的水印信号作为指证的依据，依法维护自己的合法权益，数字水印技术逐渐成为知识产权保护和数字多媒体防伪的有效手段［1］。

早期的数字水印算法多是基于空间域的方法，在嵌入水印时，只是直接改变宿主图像的像素值，多是在图像的纹理变化区域。这种方式嵌入的水印在遇到有损压缩、裁剪等攻击时极易受到破坏。而变换域算法［2］则是先把原始图像进行变换，然后把水印信息嵌入在频率系数上，水印信息是分布在图像的各个角落，稳健性大大加强。其中被广泛使用的一种变换域方法就是小波变换。

小波域的数字水印算法是MPEG-4和JPEG-2000压缩标准的核心技术［3］，应用小波域的算法在未来必将占有比较重要的席位。本文提出的是一种不可见小波变换域水印算法，通过在小波分解后的中频系数的较大值上嵌入二值信息。这种算法具有很好的稳健性，且能抵御一般的噪声攻击。

1 小波变换

1.1 相关理论

小波变换是时间和频率的局部变换，它能对高频部分进行细致观察，对低频部分做粗略观察［4］。

小波变换的定义:设f(t)是平方可积函数(即f(t)∈L2(R)R为实数集)，在满足容许性条件Cψ=为ψ(t)的傅里叶变换)下，其连续小波变换为

式中:a＞0，称为尺度;b∈(-∞，+∞)，称为位移;上标*表示取共轭，而ψ(t)为基本小波。

1.2 多分辨率分解

图像经小波分解后，可分成低频、水平、垂直及对角线频率带［5］。下一层分解是对上一层的低频频率带进一步分解出上述4个频率带，依此类推，可以进行多次小波分解。

图1是原始信号经过三级小波分解后的分解示意图，图像经过二维小波变换，被分解为LL，LH，HL，HH。其中，HH1是高频子带(细节子图)，LL3是低频子带(逼近子图);LH2，HL2，HH2，LH1，HL1，LH3，HL3，HH3是中频子带(细节子图)。

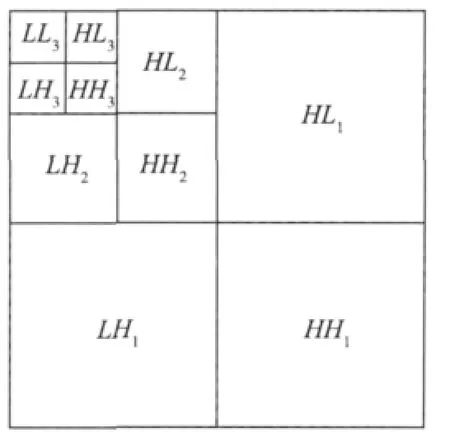
图1 三级小波分解

2 水印算法

数字水印系统包括水印嵌入器和水印检测器，主要成分为原始数据、水印本身和用户密钥。水印通常有两种:有意义水印和无意义水印。嵌入的载体可以是图像、音频和视频等。用户密钥是为了进一步提高水印的可靠性和安全性。

通过小波分解后的图像的能量主要在低频部分，在低频嵌入水印具有极好的稳健性，但是人眼对低频极其敏感，嵌入大容量的水印，会大幅度降低图像质量;高频是图像的纹理区域，嵌入高频具有很好的透明性，但是抗攻击性较差，在高频中嵌入水印，容易因受到外界有意或无意的攻击遭到破坏，降低图像的稳健性。如果采取中频嵌入，只要合理的选取嵌入系数，就能够很好地结合其优点，在保证不可见的前提下，很好地确保了水印的抗攻击能力。

2.1 水印的嵌入

水印嵌入算法的基本思路如图2所示，首先将水印进行置乱，再调制成二值序列，同时将原始图像进行离散小波分解，选取分解后的较大中频系数，然后把二值序列嵌入其上，再经过小波逆变换就得到了含水印图像。

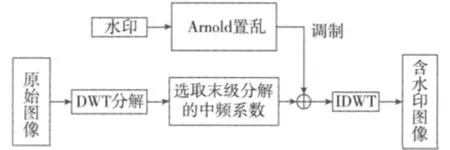
图2 嵌入水印框架图

算法的详细步骤如下:

第1步，水印的随机置乱。为防止出现大面积地嵌入同值的水印信号，也为了加强水印信息的保密性，先对水印进行Arnold置乱操作。Arnold变换是Arnold V J提出的一类裁剪变换，其二维变换定义为

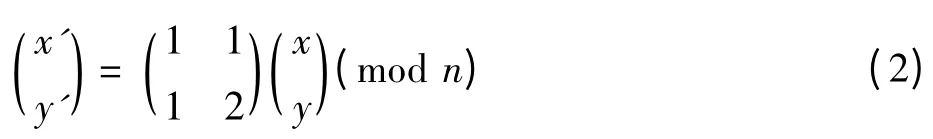
式中:x，y∈{0，1，…，n-1}:(x，y)是原始图像的像素点;(x'，y')是置乱后图像的像素点;是图像的阶数［6］。将经过Arnold变换后的水印信息调制成二值序列W(k)∈{-1，1}，将变换的次数作为密钥妥善保管。

第2步，小波分解。将原始图像进行多维小波分解，分解的原则是最终达到水印信息的尺寸和最后一级分解的频带的大小相同，然后在中频子带上选取绝对值最大的N(二值水印序列的长度)个系数，嵌入水印信息。

第3步，选取系数。水印进行的最后一级分解分为低频分量、水平分量、垂直分量和对角分量。在除低频分量之外的子带上选取较大的系数，选取系数的方法可以采用阈值法，先设置一个阈值A，选择绝对值超过A的系数，若选出的总数小于N，则降低阈值为A=A/2，继续选择系数;如果选出的总数大于等于N，则挑选结束。否则继续降低阈值，直到总数大于等于N为止。

第4步，嵌入水印。依据第一步调制的水印信息W(k)来按照式(3)进行嵌入

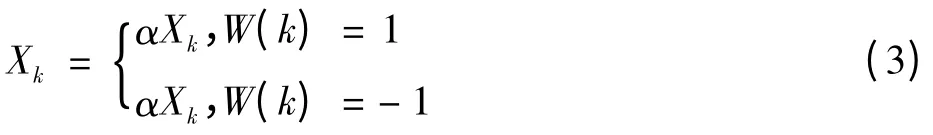
式中:α为乘性因子;Xk为嵌入水印后的系数;X0为子带上的初始系数。

第5步，将嵌入水印后的系数插回到原始中频序列中，就得到了嵌入水印后的图像。

2.2 水印的提取

水印的提取与嵌入的过程相反。具体过程如下:

第1步，对受攻击的图像和原始图像分别进行多级小波分解，和嵌入时的分解维数一致。

第2步，对受攻击后的图像最后一级分解上的中频系数进行分析，根据嵌入时的阈值，逐一挑选出改变过的系数，并将系数按式(4)来改变其值

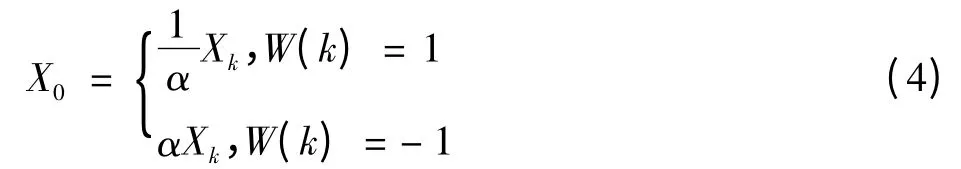
式中:α为乘性因子;Xk为嵌入水印后的系数;X0为提取出的系数。

第3步，对比系数可得到水印序列W(k)，然后通过前面使用的密钥解调，再将其进行逆置乱变换，即可提取出水印信息。

3 实验仿真结果

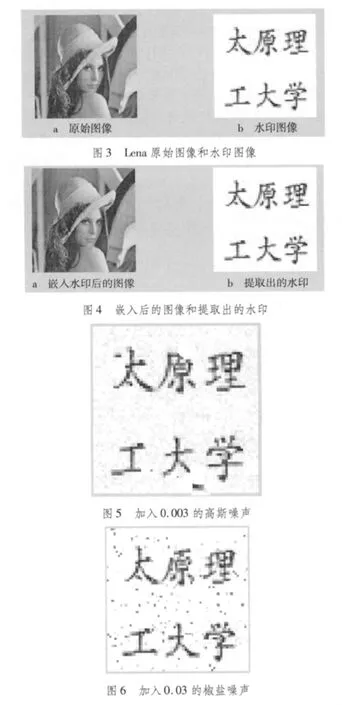
为了评估本算法的性能，选取了256×256的静态灰度级图像Lena作为原始图像，以64×64带“太原理工大学”字样的二值图像作为水印图像进行仿真实验。

对比图3和图4，原始图像和含水印的图像之间凭肉眼看不出任何失真，说明嵌入算法透明性良好。在没有任何攻击的情况下，进行了水印的提取，效果很好，嵌入前的水印和提取出的水印几乎没有失真。之后对水印算法进行稳健性检验，图5和图6分别是经过高斯噪声和椒盐噪声后的仿真结果，由结果可以看出，经过噪声攻击后，还能很好地提取出嵌入的水印信息。

4 结束语

变换域数字水印是目前的一个研究热点，是未来行业发展的趋势，但是一般的水印算法都是在低频或是高频子带上嵌入水印，虽然能很好地保证水印信息的稳健性或透明性，但是无法做到两者很好的统一。本文提出了一种新的嵌入水印的算法，选择在进行多级小波分解后的图像的较大中频系数上嵌入调制的二值数字水印信息，继承了逼进子图上的部分信息，又有着细节子图上的大部分信息，由于置乱变换次数和嵌入规则的不确定性，因此水印信息的安全性得到了充分的保证。

［1］王炳锡，彭天强.信息隐藏技术［M］.北京:国防工业出版社，2007.

［2］JAN Z K.Digital image watermarking using multilevel wavelet decomposition and human visual system［C］//Proc.ICISA 2012.［S.l.］:IEEE Press，2012:1-5.

［3］CHRISTOPOULOS C，ASKELOF J，LARSSON M.Efficient method for encoding regions of interest in the upcoming JPEG 2000 still image coding standard［J］.IEEE Signal Proceeding Letters，2000，7(9):247-249.

［4］黎洪松.数字视频处理［M］.北京:北京邮电大学出版社，2006.

［5］庄萍萍，冯桂，陈紫达.基于小波域的盲水印算法［J］.电视技术，2009，33 (S2):84-85.

［6］王琨.基于置乱加密的频率域数字图像水印算法［D］.济南:山东大学，2007.