一种改进的抗噪和旋转不变纹理图像分类算法

尚 燕，安 涛，李春明

(河北科技大学信息科学与工程学院电子系，河北 石家庄050000)

为实现基于内容的图像检索，MPEG-7标准提出了图像内容描述子的概念(如纹理描述子、形状描述子和颜色描述子等)［1-2］。如果图像表现出来的是以某一像元进行比较规则的多次重复，则可以看成是一幅较规则的纹理图像，因此纹理具有一定的区域特性。自然界的景物中，例如布匹、木纹等，大部分图像均可表现出纹理特性，因此，纹理已经成为人们用来感知世界的要素之一。纹理分析被广泛应用于图像识别、检索等，已经成为机器视觉系统的重要基础。最近几年来，研究学者们提出了各种分析方法，这些方法取得了较好的分类效果，而抗噪性是算法在实际用中应具备的重要性能，但它们往往忽视了图像噪声的影响。另一方面，虽然直接在空域计算图像的LBP直方图特征具有较好的分类效果，但其存在一些弊端，例如不能有效描述基元较大的纹理，且不具有多分辨率和抗噪性，而这些性能在实际应用中是非常重要的。为了克服这些局限，文章提出的算法先在频域对图像进行Curvelet变换，然后在空域计算其LBP直方图的方法，算法提取的特征具有多分辨率的特性且更加紧凑，能够更好地描述图像的细节和基元较大的纹理，弥补了前者的不足。另外，在现实中，如果图像混入了噪声，那么此时算法仍能够正确分类，现有的方法没有考虑图像噪声对纹理分类的影响，本文利用每个尺度的能量显著方向子带进行图像重构，再提取多分辨率LBP特征，算法具有较强的抗噪性能。

1 基于Curvelet显著方向子带的多分辨率LBP特征提取

1.1 Curvelet变换

小波理论已经被广泛应用于图像处理领域，小波变换固然表现出了很多优点，但是其小波基只有水平、垂直和对角线这3个方向，对于图像的边缘、轮廓等细节特征不能准确反映。因此，继小波变换之后，出现了很多新的多尺度几何变换，例如Ridgelet变换和之后的Curvelet变换。Curvelet变换是近年来图像处理研究的热点，因为其基函数是多方向的，具有高度各向异性，使能量更集中，能对图像的细节信息进行更稀疏表示［3］。

Curvelet变换是直接在二维连续空间R2中定义的，其基函数γ的频域表达式为

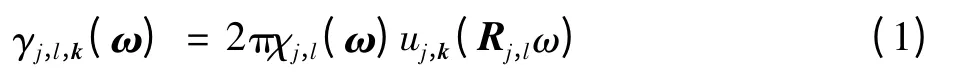
式中:ω=(ω1，ω2)T，k=(k1，k2)T∈Z2，Rj，l为旋转矩阵，其旋转角度θj，l=2πl2-j。

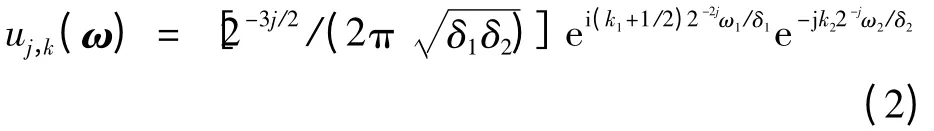
式中:δ1=14/3(1+O(2-j))，δ2=10π/9。χ为二维窗函数

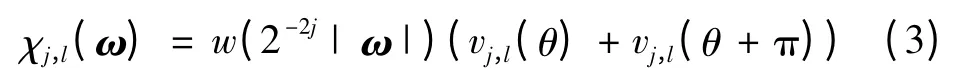
如图1a所示，Curvelet将整个频域分割成不同尺度不同方向的扇形子带，由低频子带到高频子带方向数依次加倍。通过Candes提出的Wrapping算法实现离散化，如图1b所示，不同于连续Curvelet，离散Curvelet变换将频域划分为梯形基元［4］。

图1 Curvelet变换频带划分

1.2 局部二进制模式(LBP)

令gc，g0，…，gP表示灰度纹理图像局部邻域内的p个像素，其中，gc为邻域中心像素的灰度值，gp，(p=0，…，P-1)表示半径为R的圆对称域内圆周上均匀分布的像素点灰度，不同(P，R)坐标下的圆对称域如图2所示［5］。

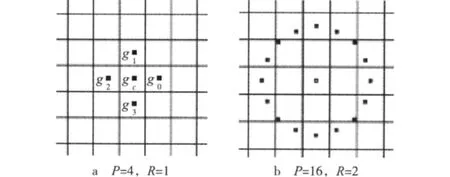
图2 不同(P，R)坐标下的圆对称域

描述局部图像纹理空间结构的LBPP，R参数定义为

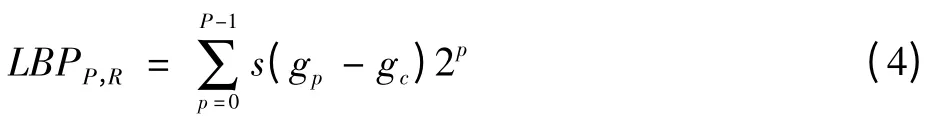
LBPP，R参数产生2P个不同的值，图像旋转时，灰度值gp将沿中心为g0、半径为R的圆周发生移动，导致LBPP，R改变，因此提出一种基于“均匀”模式的LBP算子，该算子具有旋转不变特性。定义均匀参数U，表示二进制0/1变化的次数，当U最大取2时，改进的LBP算子定义为

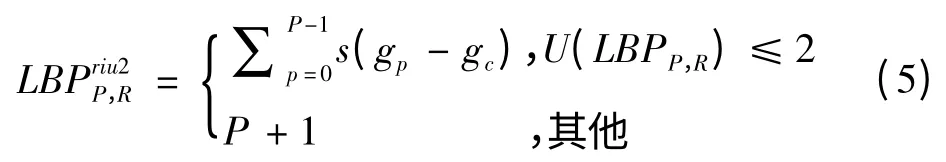
1.3 多分辨率旋转不变纹理特征提取

用LBP实现纹理分类，不能有效描述基元较大的纹理，且不具有多分辨率的特性，只通过增加R值来增加像素点达到改进分类效果的措施效果不显著，反而会使计算量增大。另外，LBP算法没有考虑抗噪性这一在实际应用中很重要的特性。针对这些问题，本文提出了一种空域和频域结合的基于Curvelet显著方向子带多分辨率LBP特征实现旋转不变纹理分类的方法。

Curvelet变换方向子带丰富，可更准确描述图像的细节信息，同时具有高度各向异性，能量更加集中，因此Curvelet变换可以更有效地表征纹理图像。算法特征提取的步骤如下:

1)设大小为N×N的纹理图像像素值f(x，y)，将其灰度值归一化到［0，1］，并对其进行(lbN-3)级Curvelet变换，因此对128×128像素的待测图像进行四级Curvelet变换，第一级为低频子带，第二级分解为16个方向子带，第三、四级均有32个子带。

2)计算各子带能量，每一尺度选取能量最大的k个子带对图像进行重构，得到的4个重构图像分别具有不同频率成分的信息，噪声主要包含在能量较小的子带中，故用大能量子带重构图像能消除大量噪声，使算法有较强的抗噪性，同时体现了多分辨率特性。设尺度i方向j子带的大小为N×N，能量计算公式为

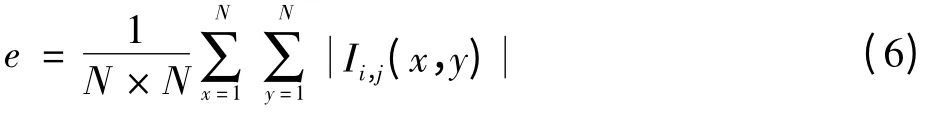
式中:i=1，2，…，lbN-3;j=1，2，…，pi/2;pi为尺度i的子带总数，对于实值Curvelet，Ⅰi，j与Ⅰi，j+pi/2子带对代表同一方向，因此，为降低运算量，取这两个子带的模值(|·|)后计算能量，并用值最大的k个子带对进行图像重构。而对于复Curvelet变换，子带各元素值为复数，实验分别取|·|和|·|2后计算能量得到的分类效果，由于复变换的计算量较大，而子带对Ii，j与Ii，j+pi/2关于原点对称，代表同一方向，因此为减少运算每个尺度只计算前pi/2个子带的能量，之后选能量大的子带对重构图像。纹理bubble及其前n(n=1，2，3，4)个尺度的重构图像以及加噪后的重构图像分别如图3和图4所示，由图3可以看出，随着尺度的增大，重构图像的频率成分越丰富且频率越高，同时如图4所示，由于各尺度选取大能量子带重构图像，因此有效消除了噪声的干扰。

3)对重构图像进行抽样，取绝对值后计算其LBP直方图。根据奈奎斯特采样定理，抽样频率应大于或等于2倍信号的最高频率，因此对包含最高频率成分的重构图像(n=4)不抽样，而对n=1，2，3的重构图像，行和列分别按抽样率1/8，1/4，1/2进行抽样。抽样后，取绝对值计算旋转不变LBP直方图，由于计算的是抽样后图像的LBP直方图，因此该LBP算子对应抽样前原图像更大尺寸的LBP算子，即可表征更大区域的图像信息，弥补传统LBP算法的不足。

4)将全部重构图像的LBP直方图组合成为特征向量。通过以上分析，该算法提取的特征更加紧凑且具有旋转不变和抗噪性能。

2 实验及结果

2.1 实验1

选用如图5所示Brodatz纹理图像进行分类实验，该纹理库共有bark、brick等13类纹理，且每类均有0°，30°，60°，90°，120°，150°，200°这7个角度。首先将原大小为512×512的图像分解为16幅128×128像素的子图，由此每类纹理可产生16×7=112幅子图。每类纹理的112幅子图中，从0°和60°的子图中各选取11幅用于训练，即训练集共包括11×2×13=286幅128×128像素的子图，其余子图均用于测试。按照上述特征提取部分描述的算法提取各子图的特征向量，将全部训练图像的特征向量集送入多项式核的支持向量机(SVM)进行训练，最后再用SVM对待侧图像进行分类。

图5 实验纹理图像

对纹理图像进行实值Curvelet变换，分类结果如表1所示，当重构子带数k=11时正确分类率达98.89%，过少或过多的子带均会降低分类率(k=2时为86.67%，k=14时为98.21%)。复Curvelet变换得到的分类结果如表2所示，由表2可知，同样在k=11时对子带元素取|·|2的分类率最高为96.15%，但相比实值Curvelet得到的98.89%分类率低2.74%。故实值Curvelet变换在重构子带数k=11的情况下，分类结果最佳，算法具有良好的旋转不变特性。

表1 实Curvelet平均正确分类率

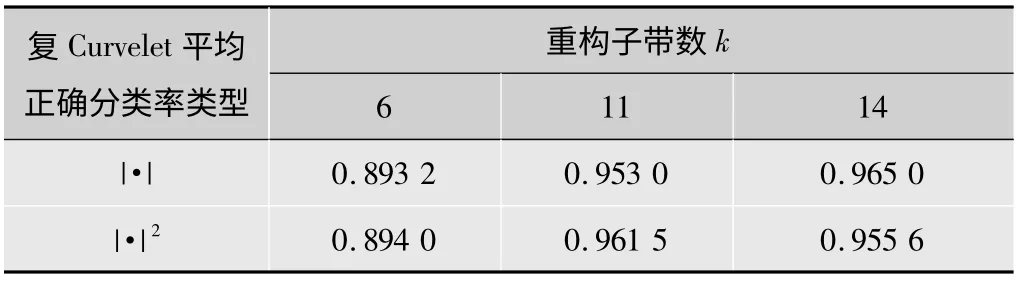
表2 复Curvelet时的平均正确分类率

将此情况下各类纹理的具体分类结果列于表3中，由此看出，全部纹理图像均可获得较高的分类率，均在96%以上，纹理基元较大的brick，bubble等纹理的分类可达100%。

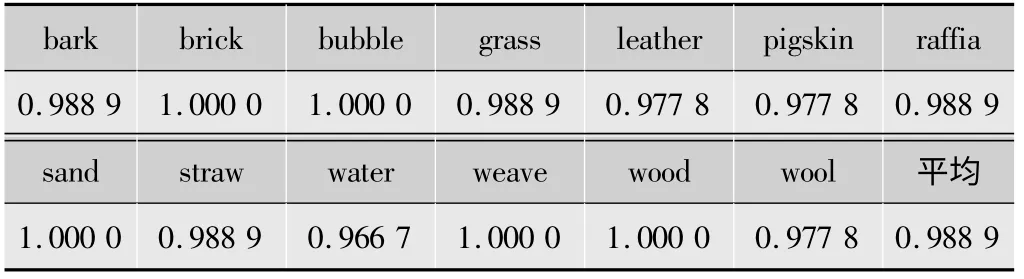
表3 各类纹理分类统计结果

2.2 实验2

为进一步实验算法的抗噪性，再对加噪后的纹理库进行分类实验。对纹理图像加不同强度的白噪声:σ=0.05，0.1，0.15(图6所示为wood及加噪σ=0.1后的图像)，再用本文算法(实值Curvelet，k=11条件下)进行分类实验，训练和测试图像的选取均与实验1相同，分类结果如表4所示。从表4可以看出，实验仍可获得较高的分类率，在σ=0.15时分类率仍可达92.74%，只比加噪前下降了6.15%。

图6 实验纹理图像

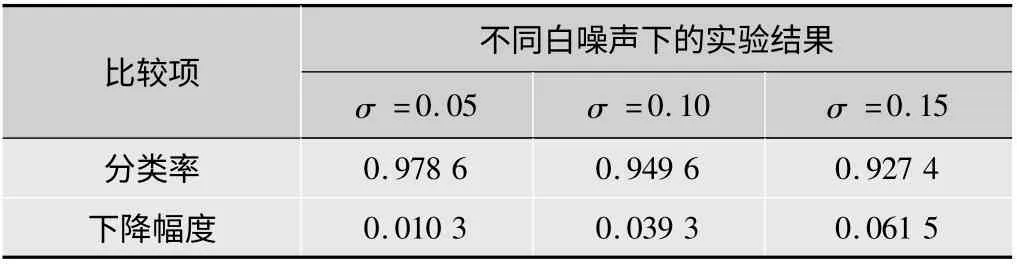
表4 本算法抗噪性实验结果

2.3 实验3

用直接在空域计算图像旋转不变LBP算子直方图的方法对原纹理图像和实验Ⅱ中的加噪图像进行分类实验，并采用相同的训练图像和测试图像，实验结果如表5所示。对原纹理图像，改进前的算法分类率为96.15%，对加噪后的图像，分类率大幅度下降，在σ=0.1和σ=0.15时分别降低10.59%和30%，而由表1和表4所示实验结果可知，改进后算法对原纹理的分类率为98.89%，分类率显著提高，而对加噪后的图像仍可获得较高的分类率，误分类率明显小于改进前算法。因此可验证本文提出改进后的算法能够有效提高分类率并且具有较强的抗噪性能。

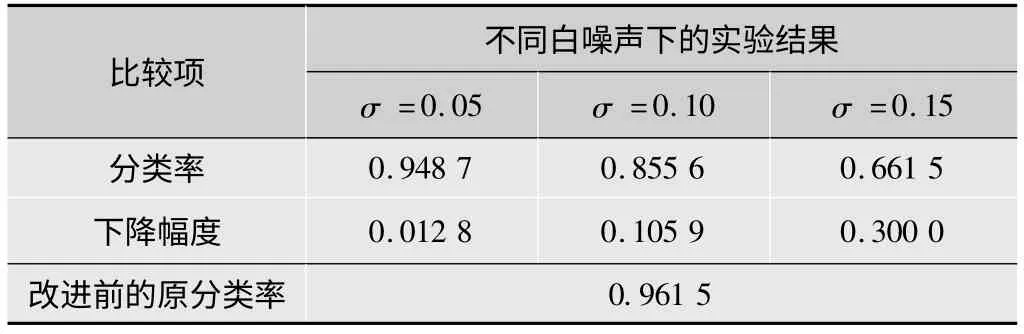
表5 改进前算法抗噪性实验结果

另外，将本算法与文献［6］用Gabor变换计算微模型参数构成宏观特征的方法对该纹理库的分类结果进行比较，文献［6］分类率为96.79%，且特征向量维数为208，用7个角度估计模型参数。而本算法的分类率比文献［6］提高了2.1%，并且特征向量维数为72，仅用0°和60°两个角度对SVM进行训练，因此本文改进后算法提取的特征更加紧凑有效，可以实现更优的分类效果。

3 结论

针对已有直接在空域计算图像LBP直方图的纹理分类算法的不足，提出一种空域和频域结合的基于Curvelet大能量方向子带多分辨率LBP特征的旋转不变和抗噪纹理分类算法。对图像进行Curvelet变换后用各尺度大能量方向子带对图像进行重构并重新抽样，进而计算抽样后重构图像的LBP直方图，直接用得到的直方图作为特征向量并用SVM实现分类。通过本算法提取的特征向量实现了多分辨率且更加紧凑，能够更准确地表征较大基元的纹理，克服了传统LBP分类法的不足。另外，本算法还具有较强的抗噪性能，这在实际应用中是非常重要的。同时结合基于最优分类超平面思想的支持向量机进行分类，实验结果表明，算法能够显著提高正确分类率，对实验纹理库的平均正确分类率可达98.89%，而且具有较强的抗噪性能。

［1］MANJUNATH B S，OHM J R，VASUDEVAN V V，et al.Color and texture descriptors［J］.IEEE Trans.Circuits and Systems for Video Technology，2001(116):703-715.

［2］BORBER M.MPEG-7 visual shape descriptors［J］.IEEE Trans.Circuits and Systems for Video Technology，2001(116):716-719.

［3］CANDES E J，GUO F.New multiscale transforms，minimum total variation synthesis:applications to edge-preserving image reconstruction［J］.Signal Processing，2002，82(11):1519-1543.

［4］CANDES E J，DEMANET L，DONOHO D L，et al.Fast discrete curvelet transforms［J］.Multiscale Modeling and Simulation，2006，5(3):861-899.

［5］OJALA T，PIETIKAINEN M.Multiresolution gray-scale and rotation invariant texture classification with local binary patterns［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，2002，24(7):971-987.

［6］GEORGE M H，MANJUNATH B S.Rotation-invariant texture classification using a complete space-frequency model［J］.IEEE Trans.Image Processing，1999，8(2):255-269.