基于Harris-SIFT算法的双目立体视觉定位

李耀云，贾敏智

(太原理工大学 信息工程学院，山西 太原030024)

1 双目立体视觉基本模型

双目立体视觉模型是模拟人的双眼从两个角度去观察立体空间的目标物体，由于几何光学的投影原理，左右两眼形成的像点在视网膜上处在不同位置。本文正是基于这种视差理论，用两台摄像机在不同位置获取同一物体的像，得到同一点的视差，再利用视差测距原理计算目标物体的深度信息［2］。双目立体视觉成像原理如图1所示。

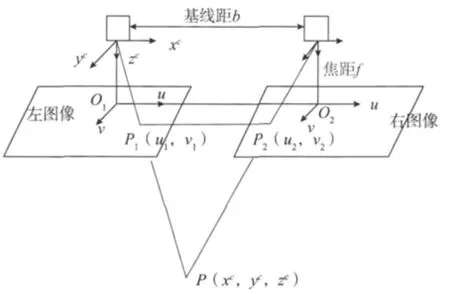
图1双目立体视觉成像原理图

图1 中两台摄像机中心的连线距离为基线距离b。左右摄像机的坐标系原点定在摄像机镜头的光心处。左右摄像机成的像平面事实上都在镜头光心后面，为了方便计算，将两台摄像机形成的像平面放在光心前方距离f处，使左图像平面坐标系O1uv的u轴和v轴与摄像机所在坐标系的x轴和y轴方向一致。左右获取的图像坐标系的原点分别与光心的连线与图像垂直交于点O1和O2。点P与摄像机坐标系原点的交线在左右两个像平面中的交点，即物体像点的坐标分别为P1(u1，v1)和P2(u2，v2)。现假设两台摄像机获得的像在一个平面，则点P的左右像点坐标的Y坐标都一样，即v1=v2。再根据相似三角计算原理得

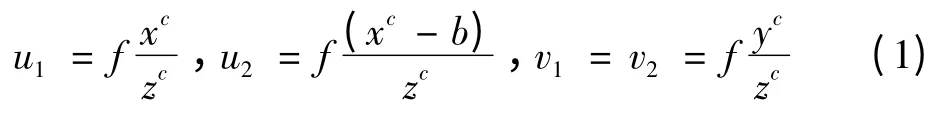
式中:(xc，yc，zc)为目标点P在左摄像机坐标系中的坐标;b为两光心间距离即基线距;f为两台摄像机焦距;(u1，v1)和(u2，v2)分别为像点在左右图像各自坐标系的坐标。

P点在两幅像平面的位置差为

由此计算出P点在左图像坐标系中坐标为

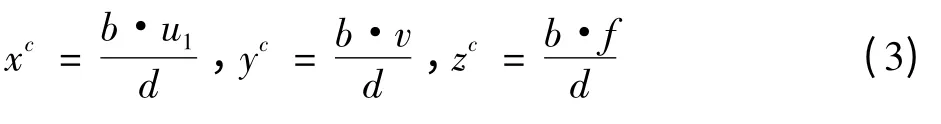
双目立体视觉系统要达到上述测距目的，必须通过摄像机获取的图像来识别目标物体，这通常需要适当的算法对其进行处理，从而实现对目标物体的识别检测。通常采用比较成熟的基于尺度空间对图像保持不变性的SIFT算法。

何西，二十五岁，骨科医生，是二叔何守二的儿子。电话铃嚎了半天，何西也没接。何东知道他在当班，就急忙往医院赶。何西刚跟着主治医做完手术，正洗手呢，一看见何东，一把把他揪到走廊里的光荣榜前面，指着一大胖脸，鱼泡眼的大幅照片问何东：“认识他吗？”

2 基于SIFT算法的目标检测

SIFT算法是David Lowe于1999年提出的一种基于不变量技术的特征检测方法，在深入的研究和完善之后，于2004年提出了一种基于尺度空间的，对图像平移、旋转、缩放、甚至仿射变换保持不变性的图像局部特征描述符［3］，该算法的特征提取过程分为以下4个步骤。

1)多尺度极值检测

高斯卷积核是实现尺度变换的唯一变换核，并且也是唯一的线性核。一幅二维图像不同尺度空间下的尺度表示为

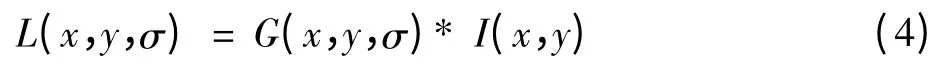
式中:G(x，y，σ)是尺度可变的高斯函数，G(x，y，σ)=;符号*表示卷积;(x，y)代表图像像素位置;σ是尺度空间因子。

为了在尺度空间稳定地检测到关键特征点，提出了高斯差分尺度空间(DOG scale-space)

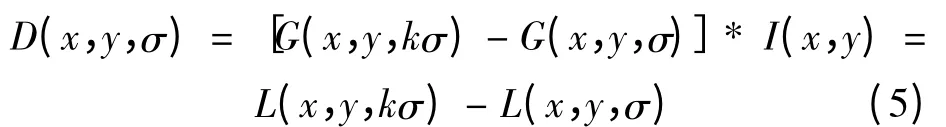
为了检测尺度空间的局部极值点，每个采样点都要与其图像域和尺度域的相邻点进行比较，判断它是否极大或极小，选择出其中的极值点。

2)精确定位极值点

定位关键点位置和尺度并消除不稳定点，对关键点的位置、尺度进行拟合，得到更精确的位置和尺度定位，同时删除具有低对比度和不稳定的边缘响应点。

3)对关键点分配方向获得旋转不变性

根据关键点的局部图像梯度方向来分配一个或多个方向。利用图像的局部特征给每一个关键点分配一个方向来描述旋转不变性。最后得到关键点邻域像素的梯度及方向

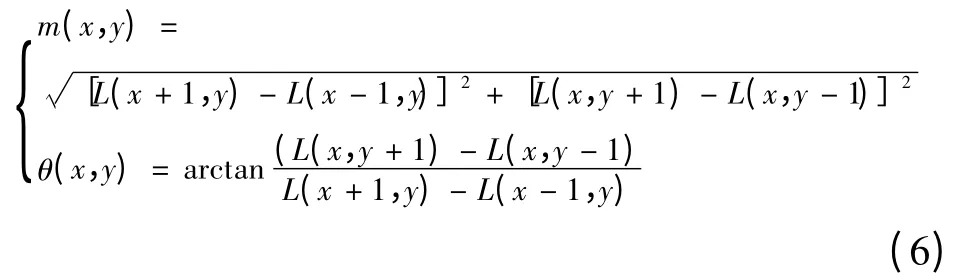
式中:尺度L为各个关键点所在尺度。

4)计算SIFT特征描述子

为了增强匹配的稳健性，对每个关键点使用4×4共16个种子点来描述，这样一个关键点就可以产生并最终形成128维的SIFT特征向量［4］。

这时当SIFT特征提取和匹配算法应用于实时性较高的双目立体视觉系统时会出现一些问题，如特征提取算子复杂性高导致算法计算时间过长;生成的特征点多而实际正确匹配的特征点只是其中一部分，影响匹配速度;SIFT算法不能准确定位角点，不能反映图像结构。机器人利用视觉采集信息需要快速反应，基于上述问题，选择更稳定快速的特征点检测Harris算子来取代SIFT中比较复杂的极值点提取算子。

3 Harris-SIFT算法

Harris角点检测算法由Chris Harris和Mike Step Hens在1988年提出，是对Moravec角点检测算子的扩展。Harris算子是一种比较有效的特征点提取算子，其值为

式中:det为矩阵行列式;tr为矩阵的迹;C为相关矩阵，即

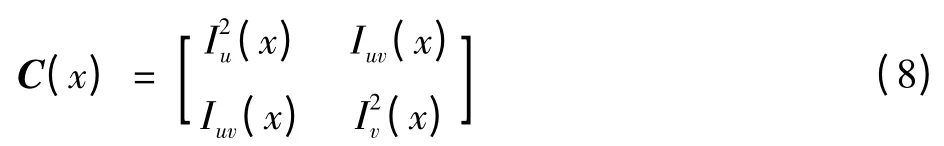
式中:Iu(x)，Iv(x)和Iuv(x)分别为图像点x的灰度在u和v方向的偏导以及二阶混合偏导;k根据经验通常取0.04～0.06。当物体某点Harris算子R大于设定阈值T时，该点为角点［5］。

Harris算子的主要特点为:对获得的灰度图像中的特征点，并计算这些点在横向和纵向上的一阶偏导数，最后获得它们二者的乘积;Harris算子中阈值取决于图像的固有属性，如尺寸、纹理等，其具体值根据经验选取。其特征点是根据该算子提取出来的角点。

Harris算子是一种比较稳定的特征提取算法［6］。这种算子的优点是:1)该算子中只用到灰度的一阶差分，计算操作简单;2)经提取的特征点分布合理，能反映图像中目标物体的结构;3)在目标物体的结构纹理处提取大量有用的特征点;4)比例、位置改变、旋转或有遮挡物时也能稳定提取特征点。

所以选用Harris算子提取特征点取代SIFT算法中的高斯卷积算法提取特征点，然后为每个提取的关键点分配方向，同时生成SIFT特征描述子，称为Harris-SIFT算法。该算法大大减少了特征提取和特征匹配的复杂度，使系统的实时性得到提高，图2和表1为两种算法匹配的效果图和数据结果。

图2 两种不同算法匹配结果

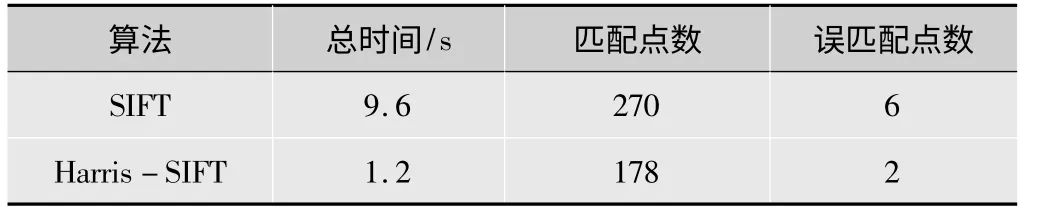
表1 匹配结果统计

如图2所示，Harris-SIFT算法匹配时特征点之间的连线明显比SIFT算法要少，图像匹配精度也提高。从表1可知，使用Harri-SIFT算法匹配时间缩短，匹配点少而精确，为应用到双目立体视觉中的图像处理提供了良好的基础。

4 目标定位的测定

根据上述结论，运用摄像机捕捉图像，然后用MATLAB7.8软件对图像进行仿真，最后通过计算得出实验数据。实验中采用针孔摄像机，组成平行双目视觉系统，基线长度为100 mm，焦距为3 mm，1/3 in(1 in=2.54 cm)CCD，CCD的面积为2.0 mm×2.5 mm，采集图片的尺寸为480×640像素。实验以墨水瓶为目标，墨水瓶模板图像与左右摄像机捕获的图像分别利用Harris-SIFT算法进行匹配。利用MATLAB7.8进行仿真，仿真的匹配效果如图3、图4所示。

图4 目标物体与右图像匹配

在左右摄像机坐标系中，标定点两个坐标横轴差值为100 mm，摄像机在同一高度，根据空间匹配点选择方法，测出左右图像中与目标匹配的特征点的坐标，然后取平均值分别得出目标物体在左右图像中的坐标分别为(795，278)，(543，278)，运用式(1)和式(2)得出墨水瓶的深度距离为285.7 mm，测得实际距离为263 mm，然后在不同距离进行测量，获得结果如表2所示，用SIFT算法测得的数据如表3所示。

表2 运用Harris-SIFT算法测试数据

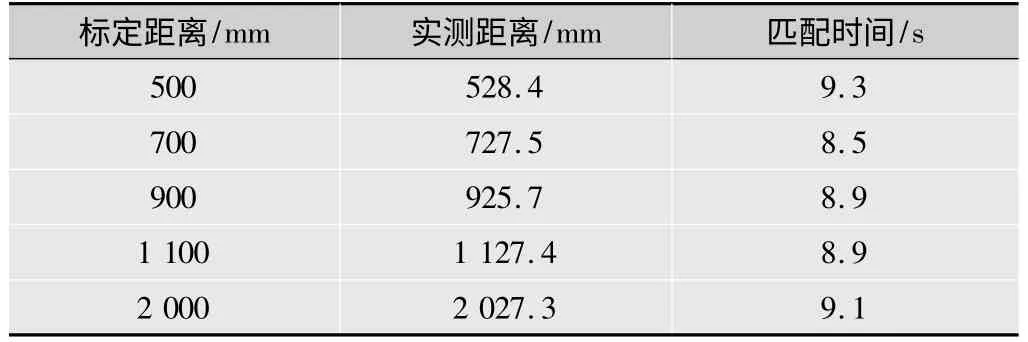
表3 运用SIFT算法测试数据

由表2、表3可知，Harris-SIFT算法应用在双目视觉中所用匹配时间大大缩短，实时性明显提高，其实测距离精度也比之前提高。分析可能造成的误差或许是由摄像机自身内部参数和摄像机摆放位置造成的。

5 结论

SIFT算法具有良好的尺度、旋转、视角和光照不变性，在图像匹配和目标识别中得到广泛应用［7］。由于这种算法所用的算子复杂性高，当应用于实时性较高的双目立体视觉系统时就会造成一些问题，如实时性不理想，测得的距离不精确等，本文应用的Harris-SIFT算法成功解决了上述问题。在空间立体中，视觉系统需要随时感知目标物体的深度距离，然后做出应有的控制策略。本文以墨水瓶为识别目标，两台摄像机保持同一水平同时获取图像，运用Harris-SIFT算法使目标物体与左右摄像机获取的图像进行匹配，获得目标物体在两幅图像中的坐标，进而计算出目标物体的方向信息和深度信息，实验所得数据在时间上有所缩短，实时性有所提高，测得距离也比之前精确，具有一定的使用价值。

［1］张春美，龚志辉，孙雷.改进SIFT特征在图像匹配中的应用［J］.计算机工程与应用，2008，44(2):95-97.

［2］刘迪.拟合人眼视觉的非均匀光照图像场景再现［J］.电视技术，2012，36(17):44-48.

［3］孟浩，程康.基于SIFT特征点的双目视觉定位［J］.哈尔滨工程大学学报，2009，30(6):649-652.

［4］李桂苓，潘榕，许树檀.立体视觉与立体成像［J］.电视技术，2012，36(2):15-18.

［5］赵钦君，赵东标，韦虎.Harris-SIFT算法及及其在双目立体视觉中的应用［J］.电子科技大学学报，2010，39(4):543-550.

［6］张德忠，贾正松.复眼立体的机器人视觉仿真［J］.电视技术，2011，35(20):35-37.

［7］LOWE D G.Distinctive image features from scale-invariant keypoints［J］.International Journal of Computer Vision，2004，60(2):91-110.