新课标下学生物理问题定性推理能力的现状分析及思考

2013-01-11艾静熊建文

物理通报 2013年10期

艾静熊建文

(华南师范大学物理与电信工程学院广东广州 510006)

1 问题的提出

通过对近三年广东高考理综物理试卷分析得出一个信息,即考生对物理问题的定性推理能力有待进一步提高.造成这种现状的原因可能是由于部分教师或学生对解决物理问题的定性推理能力的培养不够重视，平时过度依赖严谨的数学推演去求解物理问题，将物理问题数学化，忽略了对物理问题实质性的洞察和理解所致.要想真正学好物理，必须明确,数学只是学习物理的工具，不论学生数学是否优秀，只要其具备良好的定性推理能力，都有助于对物理问题实质性的洞察和理解.

2 从高考试卷分析谈现状

2.1 从高考试题的特征来看

广东高考理综试题的命制着眼于学生科学素养的培养及解决问题能力的提高.

近三年物理试题均为12道题，由4道单项选择题，5道双项选择题及3道非选择题构成，分值100分，平均用时大约50 min.这是保守估计，因为部分学生物理科的考试时间可能会被化学和生物两科占用，因此,可以说是时间紧、任务重.

高考试题虽大多源于平时训练过的习题，但不可能出原题，都是经过变形后呈现出来的，因此,在视觉上有一种陌生感.如何在最短的时间内使学生从陌生的物理情境中提炼出有效信息并应用合适的方法进行解答，提高解题的效率，是值得每位教师深思的问题.

2.2 从学生答卷出现的问题分析

(1)主观题与前几年的“3+X”考试相比总体通过率略有降低，计算题中空白卷和“零分卷”比率大幅增加,如表1所示.该问题的出现固然与考生的结构有关，过去选考物理的考生大多基础比较好，而现在则参差不齐，同时也暴露了教师在日常教学和高考备考中忽略了这个变化因素，或者没有及时采取有效措施.

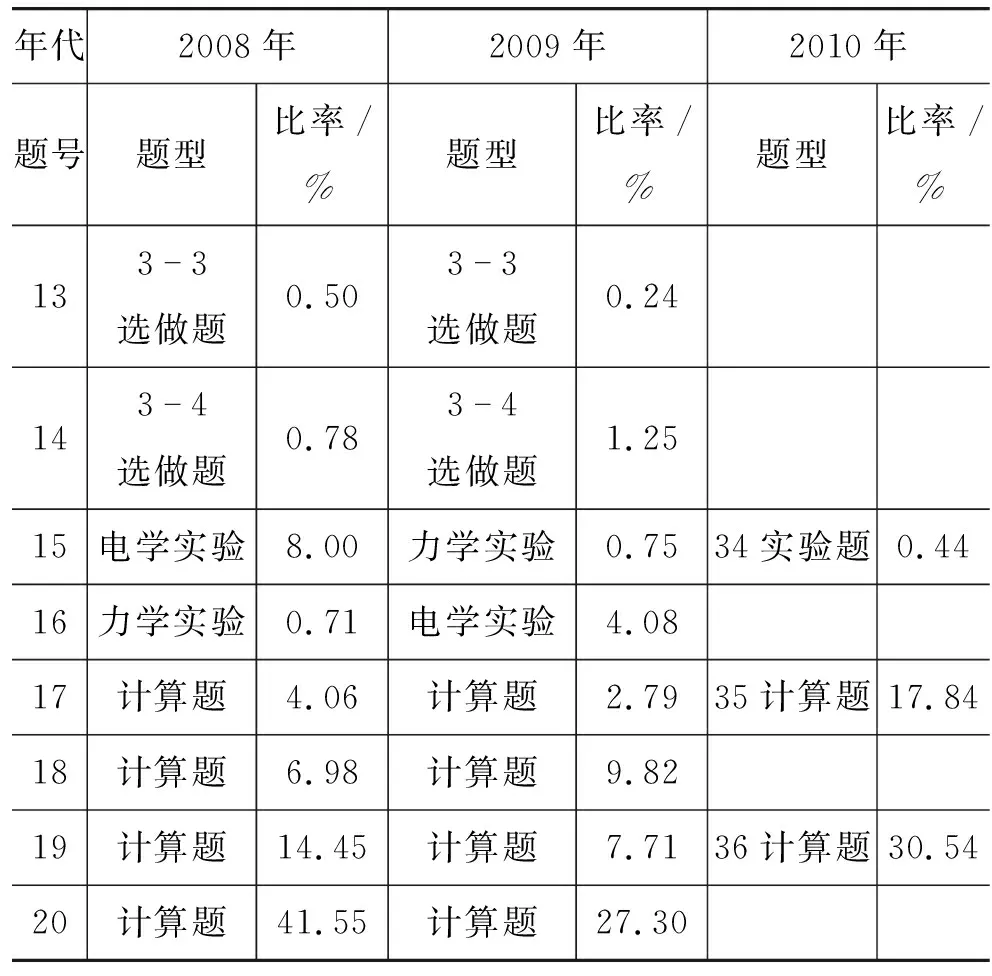
表1 2008～2010年非选择题零分比率表

高考试卷分析资料得到的统计数据显示,2010年第35题为零分的典型问题中，空白(占0分样本约58.8%)、胡乱写式子(占0分样本约16.67%)共计占到0分样本的75%以上；第36题得零分的典型问题中，空白(占0分样本约46.8%)、简单罗列公式，甚至乱用公式(占0分样本约18.0%)、错用规律解题(占0分样本约31.7%)共计占到0分样本的96.5%[1].以上统计数据值得教师深思，该数据也间接反映了学生在物理问题的定性推理能力方面的不足.

(2)理综高考题选择题都有确定的选项数目，如单选题和双选题,这就使得答题的难度大大降低.那么,是否还要依赖严谨的定量计算呢？下面以2012年广东理综物理高考题为例，说明过于重视严谨的定量计算能力的培养带来的负面影响.

【例1】(2012年高考广东理综卷第15题)质量和电量都相等的带电粒子M和N，以不同的速率经小孔S垂直进入匀强磁场，运行的半圆轨迹如图1中虚线所示，下列表述正确的是

A.M带负电，N带正电

B.M的速率小于N的速率

C.洛伦兹力对M,N做正功

D.M的运行时间大于N的运行时间

图1

说明：如果结合轨迹图先定性推理就可以分析出这是电性不同的两个带电粒子，运用左手定则简单推理就可以确定选项A正确.但习惯严谨定量计算的学生,往往因为没有分析计算完其他选项而出现对答案正确性的猜疑.这就是一味重视严谨定量计算而忽视定性推理的一个弊端，这种猜疑可能会在学生解答后续题目的心态上造成不良影响.

【例2】(2012年高考广东理综卷第16题)如图2所示，两根等长的轻绳将日光灯悬挂在天花板上，两绳与竖直方向的夹角为45°，日光灯保持水平，所受重力为G，左右两绳的拉力大小分别为

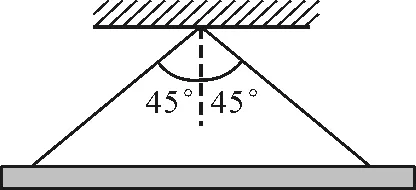
图2

说明：这道题看似需要计算，但对于定性推理能力强的学生，不需要通过定量计算就能较快地推理，得出正确选项.首先，两根绳子一样长，夹角相同，两绳所受拉力大小相等，排除选项C，其次夹角成45°，可以判断选项B正确.

可见，在解答选择题时，可以采用定性推理的方法较快地排除不正确的选项，大大节省解题的时间，在选择题中可以较好地发挥作用.在计算题中，同样可以运用定性推理的方法较快地寻找解题的突破口.2011年高考广东理综卷物理第35题第(3)问可以先运用定性分析判断，再定量计算出正确结果.

【例3】(2011年高考广东理综卷第35题)如图3(a)所示，在以O为圆心，内、外半径分别为R1和R2的圆环区域内，存在着辐射状电场和垂直纸面的匀强磁场，内、外圆间的电势差U为常量，R1=R0，R2=3R0，一电荷量为+q，质量为m的粒子从内圆上的A点进入该区域，不计重力.

(1)、(2)略.

(3)在图3(b)中，若粒子从A点进入磁场，速度大小为v3，方向不确定，要使粒子一定能够从外圆射出，磁感应强度应小于多少？

图3

分析：看完第三小问时，不少学生仅凭借对情境的熟悉就列出两种情况进行运算，得出

事实上，只需定性推理出B越小，R越大，只要求解出与磁场边界相切的最大半径对应的磁感应强度就是题中待求的值.正如李政道博士所说：“先大概估计后精确计算，这是研究物理现象的基本原则之一.”“他们通过定性的思考或半定量的试验，力求先对问题的性质，解的概貌取得一个总体的估计和理解.否则一下子陷入细枝末节，往往会一叶障目，只见树木，不见森林.”[2]

3 理解并重视定性推理能力的培养

3.1 正确认识定性推理能力

定量方法的成功使“定性”一词在物理学研究中常常被误读，如物理学家卢瑟福就曾认为“定性就是定量化不够”.在一些人的心目中，定性是出于不得已，只有高精度的定量才是最重要而且最值得追求的.

事实上，应用定性分析法解决物理问题不仅避开了繁杂的数学计算，提高了学生的解题技能，能深入到问题的本质，而且开阔了学生的视野，有利于启迪学生的思维，挖掘学生的潜能，培养学生的探索精神.美国华盛顿大学物理系L.C. McDermott教授和她的合作团队在过去的二十几年里对学生的学习进行研究，他们对单缝衍射这一光学问题，以定量计算问题和定性推理问题两种方式分别考查学生，130名参加定量计算题的学生中，70%判断正确；510名参加定性推理测验题的学生(其中包括已参加过定量测验题的130名学生)，只有10%的学生判断正确并且解释正确.他们的实验研究表明，定量计算解答能力并不是概念理解程度的可靠指标，能解答标准的定量计算题并不一定意味着真正的理解，需要定性推理和文字解释的问题对于评估学生学习综合素养来说是必不可少的[3].因此，物理问题的解答过程中应该是定性分析和定量计算相结合，只有质和量的完美结合，才能产生有效的实际价值.

3.2 “三步走”策略在日常教学中培养学生的定性推理能力

第一步：“识”.在心理上产生对定性推理能力的认同感.(1)对教师而言，教师是整个教学活动的主导者，教师自身应树立正确的认识，对定性推理能力的培养得到应有的重视；(2)长期以来，学生对数的概念根深蒂固，加上定量计算方法解决问题时有固定的模式，而定性推理分析一般无规律可循，学生不易掌握，诸多原因造成学生养成了重定量计算而轻定性推理的习惯，导致学生对物理问题缺乏实质性的理解.教师应采取有效的措施使学生转化思想，形成正确的思维习惯.

第二步：“转”.教师应有意识地进行一些针对性的训练，转变学生过度依赖严谨的数学定量计算的方式.如，在物理习题或测试中,适量地引入考查学生定性推理能力的物理问题，帮助学生改变固定的学习方式，从题海中走出来，运用科学推理方法进行物理问题的思考、分析.应用举例如下.

【例4】(2008年高考北京理综卷第20题)有一些问题你可能不会求解，但是你仍有可能对这些问题的解是否合理进行分析和判断.例如，从解的物理量单位，解随某些已知量变化的趋势，解在一些特殊条件下的结果等方面进行分析，并与预期结果、实验结论等进行比较，从而判断解的合理性或正确性.

图4

对于上述解，某同学首先分析了等号右侧量的单位，没发现问题.他进一步利用特殊条件对该解做了四项分析和判断，所得结论都是“解可能是对的”.但是，其中有一项是错误的.请你指出该项

A.当θ=0°时，该解给出a=0，这符合常识，说明该解可能是对的

B.当θ=90°时，该解给出a=g,这符合实验结论，说明该解可能是对的

C.当M≫m时，该解给出a≈gsinθ,这符合预期的结果，说明该解可能是对的

分析：本题是利用特殊条件分析和推理，定量分析来看4个选项是没有问题的，但定性推理可知，滑块B的加速度不可能大于g，所以，应选择选项D.

因此,在平时分析问题时,应避免将物理问题数学化，要了解问题的物理实质，遵循物理规律.

【例5】(2009年高考北京理综卷第20题)图5为一个内、外半径分别为R1和R2的圆环状均匀带电平面，其单位面积带电量为σ.取环面中心O为原点，以垂直于环面的轴线为x轴.设轴上任意点P到O点的的距离为x，P点电场强度的大小为E.下面给出E的4个表达式(式中k为静电力常量)，其中只有一个是合理的.你可能不会求解此处的场强E，但是你可以通过一定的物理分析，对下列表达式的合理性做出判断.根据你的判断，E的合理表达式应为