齐次线性方程组的互质正整数解在配平化学方程式中的应用

赵晓慧 戴志亮

(山东省交通运输学校，山东 泰安 271000)

配平化学方程式有很多方法，我们举一个用待定系数法配平化学方程式的例子：

铁在空气中燃烧：

(1)

设x1x2x3是三个正整数，使得：

(2)

我们可以得到

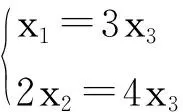
这是三个未知数，两个方程的齐次线性方程组。令x3=1，可得互质的正整数解：

因此，我们可将化学方程式(1)或(2)式配平如下：

但对于未知数较多的方程组，就不太容易求其互质的正整数解了。

一 齐次线性方程组相关理论

关于x1，x2…xn的齐次线性方程组

(3)

(我们只讨论aij(i=1,2,…m,j=1,2,…,n)为有理数的情况。)

若记

则方程组(3)也可写成向量方程A = 0

(4)的形式。

1 齐次线性方程组的互质正整数解

定义1：若存在某向量

满足向量方程(4)，则称向量x*线性方程组为(3)或(4)的一个解向量，此时，若各个分量x1，x2，…，xn均为正整数且互质，则称x1，x2，…，xn为齐次线性方程组(3)一个互质的正整数解。

定理1[1]设x1，x2，…，齐次线性方程组(3)的r个解向量，则对于任意常数，c1，c2，…，cr，则c1+c2+…+cr也是齐次线性方程组(3)的一个解向量。

定理2齐次线性方程组(3)有互质正整数解的充分必要条件是齐次线性方程组(3)有正有理数解。

证明：必要性是显然的。

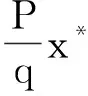
由推论可知，只要求出齐次线性方程组(3)的正有理数解，就能求出它的正整数解，进而求出它的互质的正整数解。

2 用初等行变换求线性方程组的解法

定义2[1]：线性方程组的同解变换即初等行变换是指下列三种变换：

(1)交换线性方程组的任意两个线性方程式

(2)线性方程组的任意一个线性方程式乘以非零常数k

(3)线性方程组任意一个线性方程式的常数k倍加到另外一个线性方程式上去

显然，线性方程组的初等行变换和矩阵的初等行变换是一样的，我们可以对矩阵A的初等行变换求齐次线性方程组(3)的解。

3齐次线性方程组(3) 有非零解的条件

定理3[1]已知由m个方程n个未知数的齐次线性方程组Ax=0，则齐次线性方程组(3)有非零解的充分必要条件是：秩r(A)

推论1：当齐次线性方程式的个数少于未知量的个数时，齐次线性方程有非零解。

推论2[1]：对于齐次线性方程组Ax=0，若秩r(A)=n-1，则齐次线性方程组(3)有非零解且其基础解系所含向量个数为1..

根据以上论述，对于齐次线性方程组(3)，若秩r(A)

(5)

其中xr+1，xr+2，…，xn为自由未知量。则有下列结论：

方程组(3)有正有理数解的充分条件是：在xr+1，xr+2，…，xn中，存在某个xi，使得xi,的系数全为正有理数。

若方程组(3)中存在某个方程，使得各自由未知量系数均为负数，则方程组(3)无正数解。

方程组(3)有正有理数解的必要条件是，对于方程组(3)中任一个方程，至少存在一个自由未知量，使得其系数为正有理数。

由于在化学方程式配平中，由待定系数所得的方程组一定是齐次的，且所有系数均为正整数，由结论b)，若将方程组(3)化为方程组(3)的形式后，出现某个方程各自由未知量系数均为负数，则必然是解的过程出现了错误。

对于在化学方程式配平中的齐次线性方程组，若其解只有一个自由未知量，则所得的互质正整数解是唯一的。

应用以上理论我们可以求得齐次线性方程组的互质正整数解。

例1求下列齐次线性方程组的一个互质正整数解的基础解系

解：对系数矩阵A施行初等行变换将左边4×4块化成上单位矩阵

上面最后一阵对应的齐次线性方程组为：

令(x5，x6，x7)T=(8，2，1)T，则(x1，x2，x3，x4)T=(1，8，1，1)T

令(x5，x6，x7)T=(6，1，1)T，则(x1，x2，x3，x4)T=(2，6，1，1)T

令(x5，x6，x7)T=(22，3，1)T，则(x1，x2，x3，x4)T=(6，24，9，8)T

这样，我们得到所给方程组的三个解向量：

§1=(1,8,1,1,8,2,1)T§2=(2,6,1,1,6,1,1)T§1=(6,24,9,8,22,3,1)T

显然，这三个解向量线性无关，且每个解向量的各分量互质，故所得的上述三个解向量即为所求。

二 通过齐次线性方程组的互质正整数解配平化学方程式举例

例2 配平下列化学反应方程式

CH2OH(CHOH)4CHO+[Ag(NH3)2〗OH→CH2OH(CHOH)4COONH4+Ag↓+NH3+H2O

解：设有待定系数x1，x2，x3，x4，x5，x6，使得：

x1CH2OH(CHOH)4CHO+x2[Ag(NH3)2]OH=x3CH2OH(CHOH)4COONH4+x4Ag↓+x5NH3+ x6H2O，则，我们有：

C：6 x1=6 x3

H：12 x1+7 x2=15 x3+3 x5+2 x6

O：6 x1+ x2=7 x3+ x6

Ag：x2= x4

N：2 x2= x3+x5

故我们得到下列含有n=6个未知数的齐次线性方程组：

系数矩阵：

由上述最后一矩阵可得：秩r(A) =6-1=5，含有一个自由未知量x6，且：

显然，令自由未知量x6=1，可得方程组唯一的互质的正整数解：

故所给化学反应式配平为：

.CH2OH(CHOH)4CHO+2[Ag(NH3)2]OH=CH2OH(CHOH)4COONH4+2Ag↓+3NH3+H2O

必须指出，某些化学反应式的配平系数可能不唯一，这时，齐次线性方程组系数矩阵的初等行变换法求待定系数，更显其优越性，例如：

例3配平下列化学反应方程式[2]

C6H4OHCOONa+H2O2+NaOH→C6H2O2(ONa)2·2H2O+H2O+O2↑+CO2↑

解：设有待定系数x1，x2，x3，x4，x5，x6，x7，使得：

x1C6H4OHCOONa+ x2H2O2+ x3NaOH→x4C6H2O2(ONa)2·2H2O+ x5H2O+ x6O2↑+ x7CO2↑

则:C： 7x1=6x4+x7

H： 5x1+2x2+x3=6x4+2x5

O： 3x1+2x2+x3=6x4+x5+2x6+2x7

Na： x1+x3=2x4

故我们得到下列含有n=7个未知数的齐次线性方程组：

由例1，我们已求出了它的一个互质正整数解的基础解系：

§1=(1,8,1,1,8,2,1)T§2=(2,6,1,1,6,1,1)T§1=(6,24,9,8,22,3,1)T

这样，我们得到了3组系数，配平如下：

C6H4OHCOONa+ 8H2O2+ NaOH=C6H2O2(ONa)2·2H2O+ 8H2O+2O2↑+CO2↑

2C6H4OHCOONa+6H2O2+ NaOH=C6H2O2(ONa)2·2H2O+ 6H2O+ O2↑+CO2↑

6C6H4OHCOONa+24H2O2+9NaOH=8C6H2O2(ONa)2·2H2O+ 22H2O+ 3O2↑+ CO2↑

事实上§1，§2，§3，的任意线性组合，只要满足各分量为正数且互质，都是所给反应式的配平系数。例如：++也是所得齐次线性方程组的一个解向量，且满足各分量为正数且互质，因此，也是所给反应式的配平系数：

9C6H4OHCOONa+ 38H2O2+ 11NaOH=10C6H2O2(ONa)2·2H2O+ 36H2O+6O2↑+3CO2↑

综上所述，通过求齐次线性方程组的互质正整数解可以配平较为复杂的化学方程式，例3说明存在配平系数不唯一的化学方程式。

[1] 胡健，施泱，郑龙飞.线性代数[M] . 北京：化学工业出版社，2007.52-122.

[2] 刘新华，张景晓.利用线性方程组理论配平化学方程式[J] .德州师专学报，1996，12(4)：4-5.