伪k－投射半模

王秀丽

（中国民航大学理学院，天津 300300）

伪k－投射半模

王秀丽

（中国民航大学理学院，天津 300300）

引进了伪k－投射半模的概念，并利用与k－投射半模和伪投射模相类似的研究方法，得到了伪k－投射半模的一些性质，进而实现了伪投射模和k－投射半模的一些性质到伪k－投射半模的推广.

可吸收半模；k－正则同态；伪k－投射半模；真正合列；自由半模

1 预备知识

本文中的R均表示有单位元1的半环.如果没有特别强调，所有的半模M都是指对任意的m∈M，满足1·m＝m的左R－半模，而且所有的同态都是R－同态..

下面陈述几个本文要用到的定义：［1－3］

（1）一个半环R满足左消去律当且仅当对任意

一个半模M满足左消去律当且仅当对任意

（2）半模M的一个非空子集N是可吸收的当且仅当对任意m，m′∈M，由m＋m′∈N和m∈N可推出m′∈N.

（3）一个半环R是完全可吸收的，如果R是完全可吸收半模；一个半模M是完全可吸收的当且仅当M的每个子半模N是可吸收的.

（4）设α：A→B是一个半模同态，如下定义B的子半模Imα：

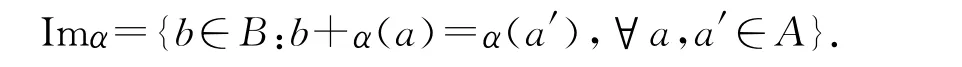
α是i－正则的，如果α（A）＝imα.α是k－正则的，如果对任意a，a′∈A，由α（a）＝α（a′）可推出

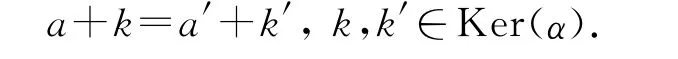
α是半单同态，如果Ker（α）＝0.

（5）序列A→B→C是一个真正合列，如果

的真正合列称为一个短真正合列.

2 伪k－投射半模

H.M.Al－Thani在文献［2－3］中已经分别给出了投射半模和k－投射半模的概念，下面将要给出伪k－投射半模的概念，并利用与伪投射模和k－投射半模相类似的研究方法［4－7］给出关于伪k－投射半模的一些主要结果.

定义2.1一个R－半模M是伪投射半模，如果对任何R－半模A，满同态f：M→A和g：M→A，存在一个R－同态h：M→M使得g＝fh，即半模同态交换图（1）可交换.特别的，如果f是一个k－正则同态时，M就被称作伪k－投射半模.

定理2.1设M是一个R－半模，则下面的条件等价：

（1）M是伪k－投射的；

（2）对任何短正合列

是正合的，则需证明：

（2）⇒（1）.显然成立.

（1）⇒（3）.对每个子半模K≤M，任意自然满同态nk：M→M／K是k－正则的.由于M是伪k－投射的，因此每个R－同态h：M→M／K可通过n k进行分解.

（3）⇒（1）.假设有一个满的k－正则同态β：M→N满足K＝Ker（β），则由分解定理［3］，存在一个满同态h：N→M／K使得hβ＝nk.设h（n）＝h（n′），由于β是满的，则有hβ（m）＝hβ（m′），其中β（m）＝n，β（m′）＝n′，因此m／K＝m′／K，即有m＋k＝m′＋k′，其中k，k′∈K.因此β（m）＝β（m′），进而h是一个同构.由假设，如果γ：M→N是一个半模同态，则hγ可通过nk进行分解：即有一个半模同态¯γ使得图（2）可交换.因此有

参照文献［8－10］有下面的结论.

定理2.2设M是一个半模，则下面的叙述是等价的：

（1）M是伪k－投射的；

（2）对任意R－半模A，任意满的k－正则同态g：B→A（其中B是M的满同态像）和满同态f：M→A，存在一个半模同态h：M→B使得f＝gh.

证明（2）⇒（1）.显然成立.

（1）⇒（2）.给定R－半模同态交换图（3），其中f是一个k－正则满同态.由于B是M的满同态像，故存在满同态n：M→B→0，因此gn：M→A→0是满的.由结论（1）可知，存在半模同态h1：M→M使得f＝gnh1，取h＝nh1：M→B，则有gh＝gnh1＝f.

定理2.3设Mi是一个R－半模，（Mi）i∈A是R－半模的集合.则⊕A M i是伪k－投射的当且仅当每个M i是伪k－投射的.

证明给定一个R－半模同态图（4），其中f是一个k－正则满同态，利用该图分别构造半模同态交换图（5）和图（6）去证明定理的结论.

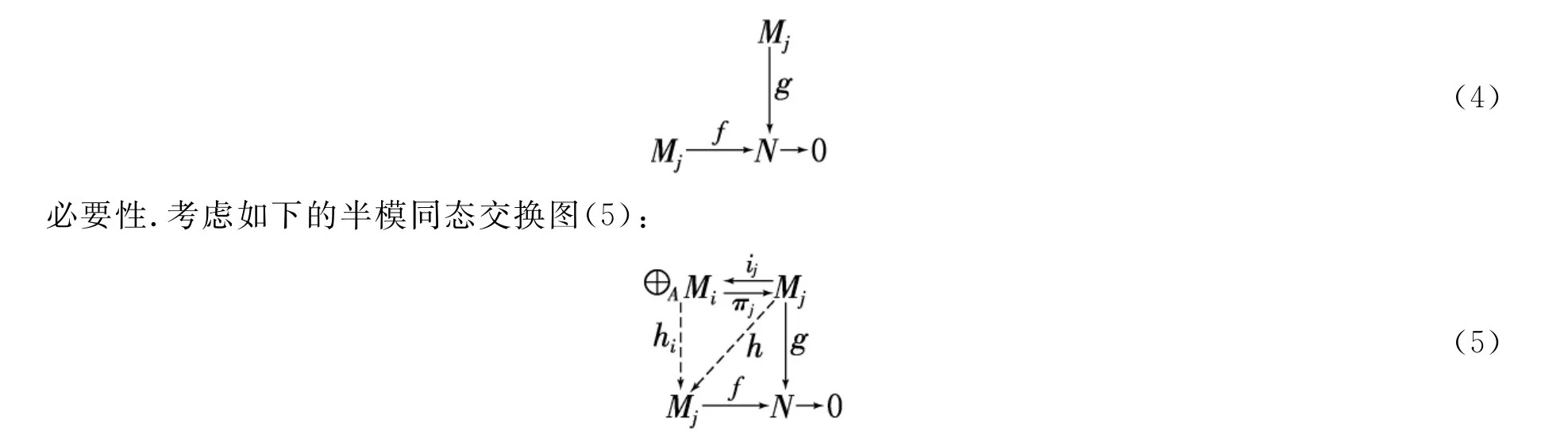
由于⊕A M j是伪k－投射的，由定理2.2，存在一个R－半模同态h i：⊕A M i→Mj使得fh i＝gπj.设h＝hii j：Mj→Mj，则fh＝fhii j＝（gπj）ij＝g（πji j）＝g I⊕AMi＝g.

充分性.考虑半模同态交换图（6），可用与上面相类似的方法证明.如果每个M j是伪k－投射的，则对每个j，存在hj：M j→M j使得fh j＝gij.设h：⊕A M i→Mj满足h（〈mj〉）＝∑ih j（mj），其中和式中有有限个mj≠0.显然h是一个R－半模同态.由于fhj＝gij，进而对每个j，有fh jπj＝gijπj，所以fh＝g.

定义2.2［3］一个R－半模P是k－正则的，如果存在一个自由R－半模F和一个满的R－同态f：F→P使得f是k－正则的.

定理2.4设P是一个k－正则半模，则下面的结论等价：

（1）P是伪k－投射的；

（2）P是投射的.

证明（1）⇒（2）.假设P是伪k－投射的.由于P是k－正则的，则存在一个自由R－半模F和一个k－正则满R－同态α：F→P.又由假设P是伪k－投射的，则存在R－同态β：P→F使得βα＝Ip.设｛ek：k∈K｝是F的一组基，如果x∈P，则β（x）∈F.因此可记

其中λk∈R且对几乎所有的k，λk＝0.定义βk（x）＝λk，则βk是R－同态.由于α是满射，所以｛p k：k∈K｝生成P，其中p k＝α（ek）.而且，如果x∈P，则

由定理2.1可知P是投射的.

（2）⇒（1）.显然.

［1］GOLAN J S.The theory of semirings with applications in mathematics and theoretical computer［M］.London：Longman Science＆Technical，1992：54－79.

［2］HUDA MOHAMMED，ALTHANI J.A note on projective semimodules［J］.Kobe J MATH，1995，12：89－94.

［3］HUDA MOHAMMED，ALTHANI J.k－projective semimodules［J］.Kobe J MATH，1996，13：49－59.

［4］AHSAN J，SHABIR M.Semirings with projective ideals［J］.Math Japonica，1993，38（2）：271－276.

［5］ROTMAN J.An introduction to homological algebra［M］.San－Francisco，London，New York：Academic Press，1979：25－60.

［6］TAKAHASHI M.Extentions of semimodulesⅡ［J］.Math Sem Notes，1983，11：83－118.

［7］佟文廷.关于伪投射模［J］.数学研究与评论，1996，16（3）：355－358.

［8］王秀丽.Ni－内射半模及其性质［J］.纯粹数学与应用数学，2010，26（2）：316－318.

［9］赵春娥，杜先能.关于伪投射模的一些讨论［J］.大学数学，2006，22（3）：100－102，.

［10］马丽丽，张朝凤，张永正.有限维模李超代数U的导子代数［J］.东北师大学报：自然科学版，2011，43（2）：1－6.

Pseudok－projective semimodules

WANG Xiu－li
（Science College，Civil Aviation University of China，Tianjin 300300，China）

In this paper，the concept of pseudok－projective semimodules is introduced，then on the similar method tok－projective semimodules and pseudo－projective modules，it gets some good properties of pseudok－projective semimodules，which realize the generalizations of some properties of pseudo－projective semimodules andk－projective semimodules to pseudok－projective semimodules.

subtractive semimodules；k－regular homomorphism；pseudok－projective semimodules；proper exact sequence；free semimodules

O 153.3

110·21

A

1000－1832（2012）01－0041－04

2011－06－30

天津市自然科学基金资助项目（08JCYBJC13900）；中国民航大学理学科研基金资助项目（2010kys06）.

王秀丽（1976—），女，硕士，讲师，主要从事环与代数研究.

陶 理）