基于AR模型谱估计的调制方式自动识别算法

孙钢灿，王忠勇

(郑州大学 信息工程学院，河南 郑州 450001)

调制信号自动识别分两步完成，分别是特征值的提取和分类器的设计.其中，特征值的提取是关键问题.目前，已提出的调制信号识别特征很多，Azzouz[1-3]等人提出了基于信号时域瞬时特征的方法，此方法首先要对中频数字采样序列进行希尔伯特变换，然后计算出信号的瞬时特征值，在此基础上进一步计算瞬时特征的统计量.Swami[4-7]等人提出了基于高阶累积量的方法，此方法需要在基带信号上完成，要求准确估算出信号的载波频率、初始相位和符号速率等.另外，最近研究比较多的还有基于接收信号重构星座图完成调制识别的方法[8-9].上述方法都是在时域完成的，计算步骤较复杂，需要的先验信息较多.

曹志刚[10-11]等提出了基于信号的功率谱进行调制信号的自动识别，通过经典谱估计方法得出信号的功率谱，在此基础上提取出若干特征值.但是，由于经典谱估计的方差性能较差、分辨率较低、频谱为离散谱线等固有缺点，导致在信噪比较低或采集的数据点数较短时，容易有干扰峰值的出现，提取特征参数时容易发生错误.为此，本研究提出了基于现代谱估计的方法，通过现代谱估计方法得到信号的功率谱，提出了谱峰的个数和谱峰的峰态量两个新特征值并给出了新特征值的计算方法，实验证明新特征值在低信噪比情况下识别性能很好.

1 基于现代谱估计的调制信号功率谱

1.1 现代谱估计和经典谱估计的区别

经典谱估计方法的方差性能较差，分辨率较低，估计出的谱不够平滑.方差性能差的原因是无法实现功率谱密度原始定义中的求均值和求极限的运算；分辨率低的原因是对周期图法假定数据窗以外的数据全为0，对自相关法假定了在延时窗以外的自相关函数全为0；估计出的谱不够平滑是因为不具备现代谱估计方法中的有理公式来表示功率谱.为了克服这些不足，提出了现代谱估计的方法.

经典谱估计的分辨率反比于使用的信号长度，由信号的时宽-带宽积可知，长度为N的信号，若抽样间隔为T，抽样频率为Fs，那么由离散傅里叶变换(DFT)作谱分析时，其分辨率粗略为Fs/N，即窗函数主瓣的宽度，所以采用经典谱估计算法时，如果分辨率要求很高的话，就要很长的数据长度，要求样本足够长，同时也增加了计算量.而现代谱估计可以不受此限制，因为对给定的数据，虽然其估计出的自相关函数也是有限长，但现代谱估计的一些方法隐含着数据和自相关函数的外推，使其可能的长度超过了给定的长度.AR模型就是在最小方差意义上对数据进行拟合.由于AR模型是一个有理分式，因而估计出的谱要比经典法的谱平滑，这样有利于识别谱峰及区别不同信号的谱峰，通过信号的谱峰个数和尖锐程度提取调制识别的分类特征值.在基于模型的谱估计算法中，自回归模型是一个全极点的模型，易于反映功率谱中的峰值，所以本研究采用AR模型谱估计[12].

1.2 基于现代谱估计的信号功率谱

首先，求信号的功率谱、信号的平方功率谱和信号的高次方谱等，然后提取频域的分类特征值.

信号的功率谱直接反映调制信号中的各频率分量的功率分布，在调制信号中频载波处会有谱峰出现，所以根据中频信号功率谱的谱峰个数以及谱峰的峰态量可以区分调制信号的类型，常用数字调制信号中的单峰信号有MPSK，双峰信号有2FSK，多峰信号有MFSK(M>4).

图1和图2是使用经典的周期图法和基于AR模型的现代谱估计方法计算出的功率谱，信噪比为5 dB，采样点数为4 096，AR模型的阶数为30.可看出，在使用经典功率谱估计方法时，可以用幅度较大的离散谱线单频点个数用来区分MPSK和MFSK信号，没有较大单频点的为MPSK信号，单频点的个数代表了MFSK信号的调制阶数.因为有干扰离散谱线的存在且有时会比较大，接近于载波的单频值幅度，所以离散谱提取的阈值设定往往比较困难，太高了容易漏掉单频点，太低了又容易错把干扰信号频点误判为调制信号单频点.使用基于AR模型的现代谱估计方法计算出的谱峰较为平滑，在单频分量处会出现较明显的谱峰，更容易计算出谱峰的个数，通过选择合适的AR模型的阶数，干扰谱线被平滑掉了，所以不易发生误判.

图1 2FSK和4FSK信号功率谱

图2 2PSK和4PSK信号功率谱

对信号进行偶数次幂操作，然后计算其功率谱，可以有效分辨MPSK信号.信号平方谱即为信号平方后的功率谱.由于平方运算产生很大的直流分量，所以一般忽略功率谱的零频值和零频附近频值.平方谱反映调制信号倍频后的频谱功率分布特性，对载波只有π跳变的BPSK信号，平方谱在2倍载频处有很强的单频分量，而其他的MPSK信号则无此特征.同样道理，如需分离更高调制阶数的MPSK信号，如4PSK和8PSK信号，可以按同样方法再次对信号进行取平方谱运算.

图3为使用两种方法下MPSK信号平方的功率谱，信噪比为5 dB，采样点数为4 096，AR模型的阶数为30.从图3中可看出，2PSK信号的单频值较为明显，两种方法功率谱估计方法下都很容易提取出来，使用基于AR模型的谱估计方法更容易提取出4PSK信号的谱峰个数.由于2PSK的平方谱含有很强的单频值，基于AR模型谱估计方法的谱峰较4PSK更尖锐.下面定义峰态量来表征谱峰的尖锐程度，可以通过峰态量来区分两种调制方式.

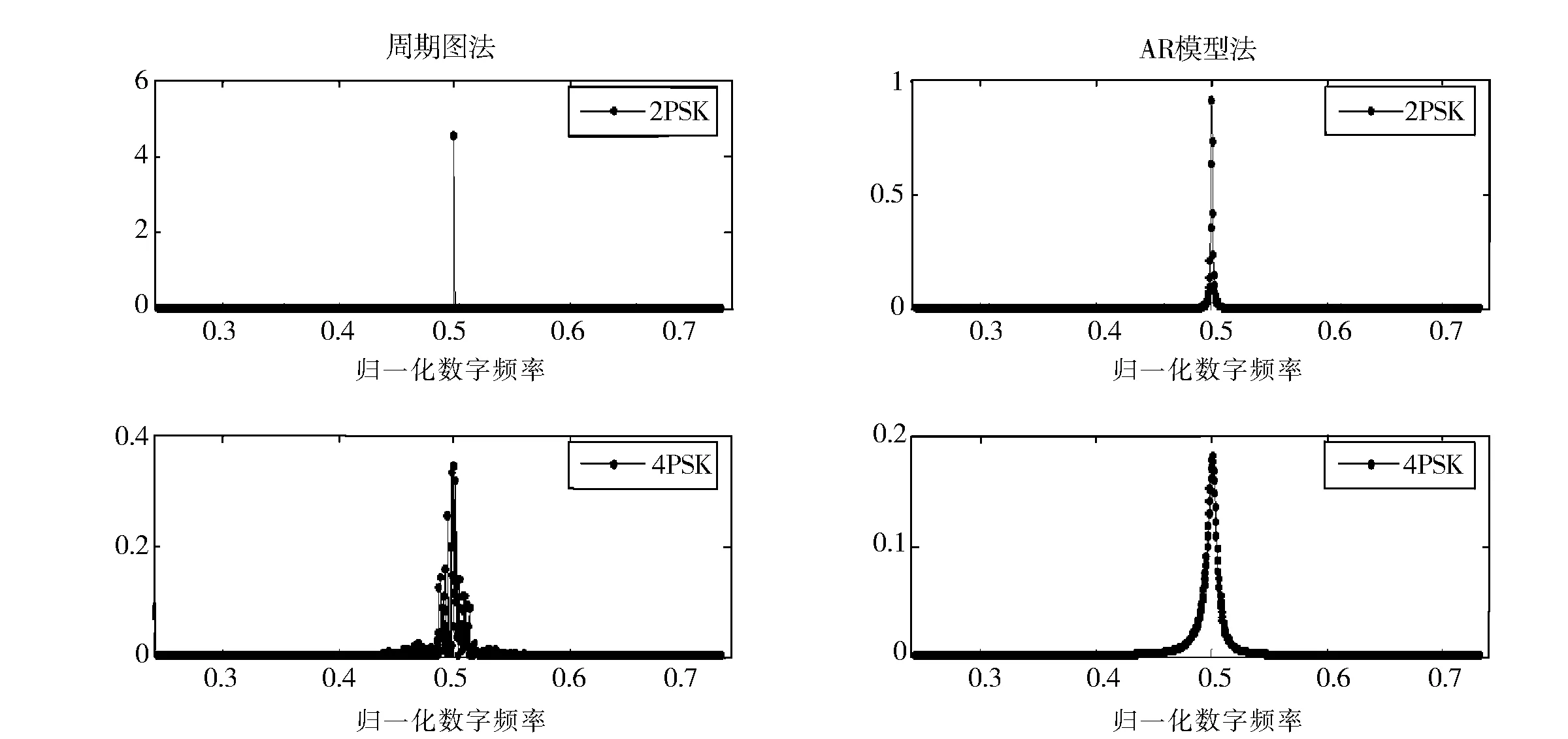
图3 MPSK信号平方的功率谱

2 特征参数的提取

通过观察发现，基于AR模型的功率谱更易于提取分类特征参数，下面给出提取两个新特征参数的数学表达式.

2.1 信号功率谱的谱峰个数

信号谱峰的个数提取是调制识别的关键，如果提取错误就会发生误判.根据是单峰还是多峰，可以区分出MPSK信号和MFSK信号，根据峰的个数可以进一步判断出MFSK信号的调制阶数.首先，需要通过基于AR模型的现代谱估计方法计算出功率谱.从功率谱的图示中可看出，谱峰应具备两个条件，一是大于某个阈值，二是在某一频段内是极大值，其左右的频段在一定范围分别为单调递增和单调递减.设p(n)为功率谱，所以谱峰的计算公式可简单表达如下：

(1)

其中，p(i)表示第i点功率值，max[·]表示求最大值，mean[·]表示求均值，n表示抽取的功率谱的点数，l为判断极大值点的信号段长度.同时满足上面两式的点即为一个谱峰，搜索完成后可给出谱峰个数.

2.2 信号功率谱的峰态量

信号谱峰的峰态量主要用来刻画峰的尖锐程度，由此可以判断信号频谱中有没有单频分量.2PSK信号的平方谱中含有一个单频分量，而4PSK信号的平方谱中则不含有单频分量，故可以用来区分不同阶数的MPSK信号，峰态量的计算表达式如下：

(2)

其中，sum[·]表示求和操作，i为峰值点，l1和l2代表了求和的范围且l2大于l1，具体值根据抽样序列的长度和AR模型的阶数来确定，表达式中分母大于分子，Ku越接近于1，表示该谱峰越尖锐.在实际应用时，设定某个门限阈值，当计算出的峰态量大于该阈值时可认为该谱峰为一个单频分量.

3 计算机仿真

为了验证本研究所描述的分类特征值提取方法的有效性，选择4种不同类型的信号，分别为2PSK、4PSK、2FSK和4FSK.载波频率fc、抽样频率fs和符号速率rs分别设为150.0 kHz、1 200.0 kHz和12.5kHz.2PSK和4PSK信号的载波相位分别为(1-θ)π(θ=0，1)和θπ/2(θ=0，1，2，3)，2FSK和4FSK信号的载波频率分别为fc±θrs和fc±θrs(θ=1，2).所有的通信信号都是带限的，2PSK、4PSK、2FSK、4FSK的带宽范围分别为75 kHz、75 kHz、100 kHz和100 kHz.信道为加性高斯噪声信道，噪声加载到调制信号上.

对以上各种数字调制信号抽取4 096个采样点，每种个调制类型在每个信噪比上实验500次，然后计算出识别率结果.基于AR模型计算采样信号的功率谱，AR模型的阶数选择为30.公式(1)中的长度l选择为10点，公式(2)中的l1和l2分别选择为10和20，峰态量的门限值设定为0.8.信噪比范围为-2～6 dB，大于或等于5 dB时识别正确率为100%，表1给出了4 dB和-2 dB时的识别率结果.

识别步骤：

(1)计算信号功率谱和谱峰个数，谱峰数大于2，则该信号为4FSK，进入第3步；谱峰数等于2，则信号为2FSK，进入第3步；谱峰数小于2，则信号为MPSK，进入第2步.

(2)计算信号平方的功率谱，去掉直流部分后计算信号谱峰的峰态量，若峰态量大于阈值0.8，则信号为2PSK，反之，则信号为4PSK，进入第3步.

(3)识别结束.

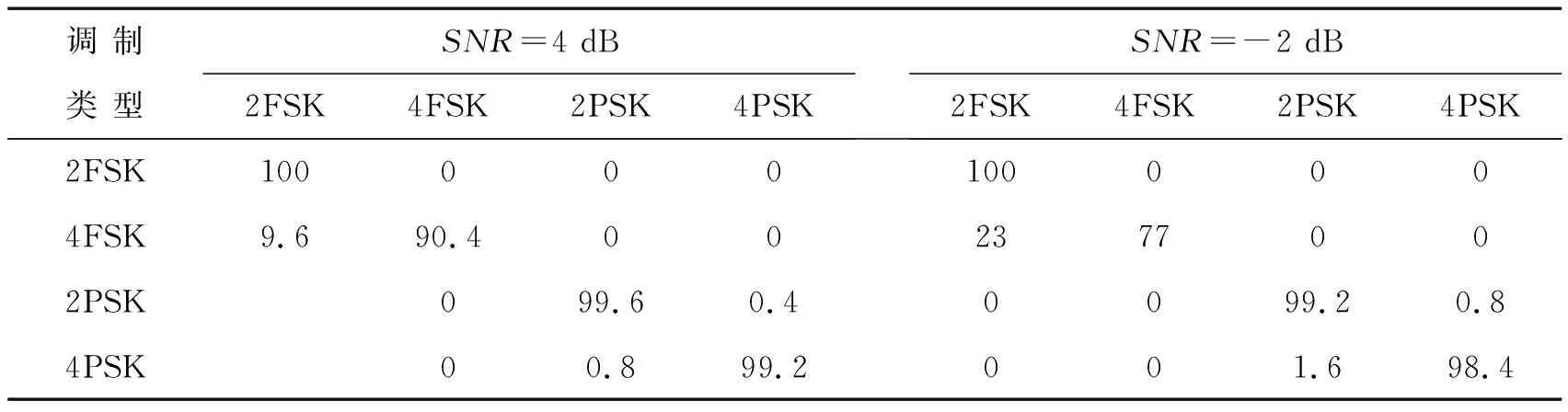
表1 不同信噪比下系统识别率

通过识别率数据可看出，当SNR=4 dB时，开始出现识别错误，其中4FSK容易误判为2FSK，2PSK和4PSK也有少量的互相误判.如信噪比继续变小，识别率下降；当SNR=-2 dB时，除4FSK较多地被误判为2FSK外，其余的仍然能保持较高的识别正确率，充分证明了新特征值的有效性和顽健性.

4 结论

在调制信号分类识别的研究中，基于频域特性的方法直观简单，有很好的实用前景.本研究提出了基于AR模型的现代谱估计的调制识别算法，给出了谱峰个数和峰态量的计算公式.计算机仿真证明，新方法简单易用且具有很好的抗干扰特性，适用于所有阶数MPSK和MFSK信号的识别.在实际应用中，可以结合已有文献提出的特征值一起使用，完成更多种调制信号的识别.

参考文献：

[1]Azzouz E E，Asoke K N.Automatic identification of digital modulation[J].Signal Processing，1995,47(1):55-69.

[2]Asoke K N，Azzouz E E.Algorithms for automatic modulation recognition of communication signals[J].IEEE Trans on Communications,1998,46(4):431-436.

[3]Asoke K N，Azzouz E E.Automatic analogue modulation recognition[J].Signal Processing, 1995(46):211-222.

[4]Swami A,Sadler B M.Hierarchical digital modulation classification using cumulants[J].IEEE Trans on Communications,2000,48(3):416-429.

[5]Swami A,Sadler B M.Modulation classification via hierarchical agglomerative cluster analysis[J].IEEE Signal Processing Workshop on Signal Processing Advances in Wireless Communication,1997(8):141-144.

[6]Yang S Q,Chen W D.Classification of MPSK signals using cumulant invariants[J].Journal of Electronics,2002,19(1):99-103.

[7]Orlic V D,Dukic M L.Multipath channel estimation algorithm for automatic modulation classification using sixth-order cumulants[J].Electronics Letters,2010,46(19):1348-1349.

[8]张路平,王建新.MQAM信号调制方式盲识别[J].电子与信息学报,2011,22(2):332-336.

[9]刘明骞,李兵兵,赵雷.多径信道下OFDM信号子载波的调制方式识别[J].西安电子科技大学学报:自然科学版,2011,38(5):26-34.

[10]范海波,杨志俊,曹志刚.卫星通信常用调制方式的自动识别[J].通信学报，2004,25(1)：138-149.

[11]赵春晖,杨伟超,马爽.基于广义二阶循环统计量的通信信号调制识别研究[J].通信学报,2011(32)：144-150.

[12]胡广书.数字信号处理——理论算法与实现[M].北京:清华大学出版社,2003:527-580.