复Banach空间上推广的Roper-Suffridge算子的性质

崔艳艳，汪 叶

(1.周口师范学院 数学与信息科学系，河南 周口 466001;2.河南大学 数学与信息科学学院，河南 开封 475001)

自Roper-Suffridge算子[1]引入以来,对该算子及其推广的研究已有了许多成果.在前人的研究基础上，本研究在复Banach空间中讨论了推广的Roper-Suffridge算子保持双全纯映照子族的其他性质.用X表示具有范数‖x‖的复Banach空间,B表示X中的开单位球,S(D)表示单位圆盘D上正规化双全纯映照的全体.Cn中单位球上强β型螺形映照的定义由Hamada与Kohr[2]给出,徐庆华和刘太顺给出了任意有限维复Banach空间单位球上的情形.

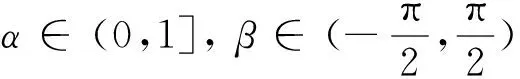
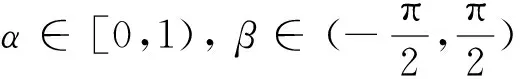
1995年,Chuaqui建立了Cn中单位球Bn上强α次殆星形映照[6]的概念,现将其推广到复Banach空间单位球上.

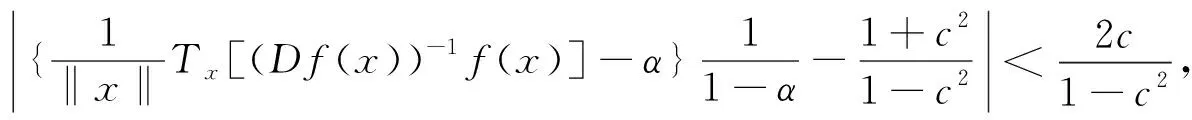
1 主要结论及其证明

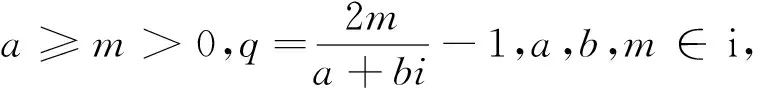
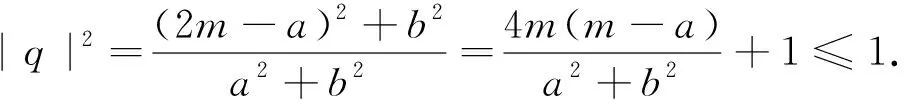
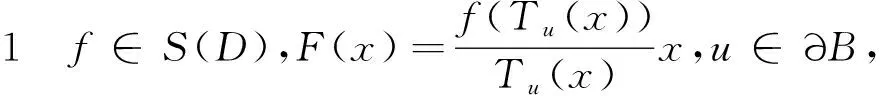
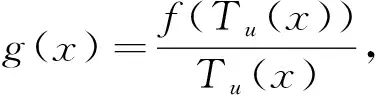
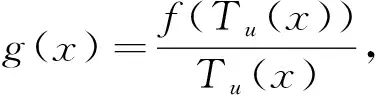
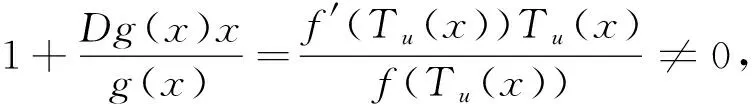
(1)

在定理1中若取β=0则得到相应的强星形映照的结论.

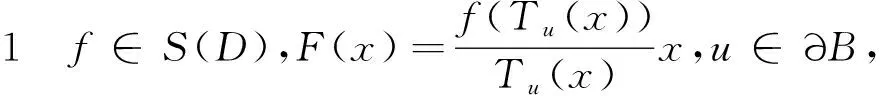
与定理1同理可得相应的强α次殆星及α次强β型螺形映照的结论.

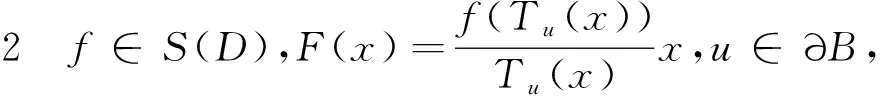
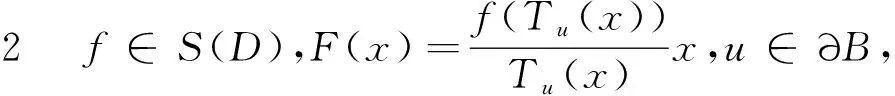
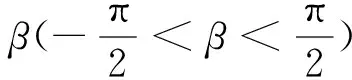
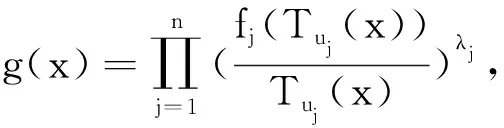
在定理3中,令β=0则得到相应的α次殆星形映照的结论[7];令α=0则得到相应的β型螺形映照的结论,若令α=β=0则得到相应的星形映照的结论.

参考文献：

[1]Roper K A,Suffridge T J.Convex mappings on the unit ball ofCn[J].J Anal Math,1995(65):333-347.

[2]Hamada H,Kohr G.The growth theorem and quasiconformal extension of spirallike mappings of type [J].Complex Variables,2001(44):281-297.

[3]徐庆华,刘太顺.正规化双全纯映照的增长和掩盖定理[J].数学年刊,2009,30A(2):213-220．

[4]冯淑霞.多复变函数的几类全纯映射族[D].北京:中国科学技术大学，2004．

[5]Gong S.Convex and Starlike Mappings in Several Complex Variables [M].Boston:Kliwer Academic Publishers,1998.

[6]Chuaqui M.Applications of subordination chains to starlike mappings in[J].Pacif J Math,1995(168):33-48.

[7]刘小松.多复变数几何函数论中某些双全纯映照子族的性质[D].北京:中国科学技术大学，2004．