基于改进AHP的授课教师教学质量分析

周永卫，范贺花

(郑州航空工业管理学院 数理系，河南 郑州 450015)

近年来，随着高校的不断扩招，提高高校的教学质量已经成为全社会共同关心的问题.为提高教学质量，各个学校也在不断地进行教学改革，教师挂牌就是近年来许多高校实施的教学改革措施之一.具体措施是学校在安排下学期的教学任务时，对同一门课程安排在同一时间上课.同时，对任课教师提出要求，必须由两名以上的主讲教师网上挂牌，主讲教师的基本信息如性别、年龄、学位、职称、科研水平、拟授课方式、往年评教结果、教育经历、工作经历、授课经历等也同时在网上公布，学生根据教学计划以及教师的基本信息在全校范围内选择授课教师，不再局限于教学班.实施挂牌上课的教师按选课学生数计算开班工作量，与津贴挂钩，选课人数不足20人不予开课.这一举措有助于真正形成优胜劣汰的竞争机制，优化师资配置，提高教学质量.

上海财经大学在2001年就率先推出这一举措，在该校也收到了很大实效.首先，优秀教师多上课、开大班，学生受益面广，有利于提高办学效益，缓解扩招之后师资紧缺的矛盾.同时，通过对“中选”和“落选”情况的具体分析，调整课程设置和师资配置，使其更加优化和合理.

从学生方面来讲，在选课时他们都希望选到适合自己的任课教师，但又没有一个统一的标准，只是跟着感觉走，甚至是人云亦云，看别的同学选哪位任课教师，自己就也选这位教师.更有甚者，有的学生根本不看任课教师是哪一位，不负责任地随便乱选.总之，学生对授课教师的遴选不仅带有很大的盲目性，而且也违背了学校教学改革的初衷.事实上，这是一个典型的多层次多因素综合评价问题，对于这类问题，评价的方法很多，其中应用较广也最为简单有效的方法是层次分析法，即AHP[1]模型.

1 改进层次分析法的主要思路以及原理根据

AHP是由美国著名运筹学家、匹兹堡大学教授Saaty 于20世纪七十年代中期提出的一种定性与定量相结合的决策分析方法，该方法已被广泛应用于经济分析、路径规划、企业管理和政策分析等领域[2-5]，并且取得了很好的效果.AHP的重要步骤之一就是构造成对比较矩阵，但由于人为判断的主观性和片面性，所构造的成对比较矩阵出现不合理结果的可能性较大[6-7]，故必须进行一致性检验.一致性检验较复杂，一旦一致性检验不通过，要对成对比较矩阵不断进行人工调整，直至满足一致性要求，这样工作量大且在调整时带有一定的盲目性.

文献[8]对层次分析法进行了改进，利用文献[8]的结果，当构造的成对比较矩阵不是一致性矩阵时，可以从原成对比较阵出发，结合问题的实际意义，通过对原矩阵进行初等变换，建立起新的一致成对比较矩阵. 在这个新的一致成对比较矩阵中，包含了决策者所有的判断参数，不再需要一致性检验就能得到合理的最终决策.

首先引入两个定义：

定义1设A=(aij)n×n是一成对比较矩阵，且若aij=aik·akj(i，j，k=1，2，…，n)，则A是完全一致性矩阵.

定义2设A=(aij)n×n和B=(bij)n×n是成对比较矩阵，C=(cij)n×n为矩阵A与B的Hardmard积，即cij=aij·bij(i，j=1，2，…，n)，记为C=A⊗B.

定理1矩阵P=(pij)n×n=A(1)⊗A(2)⊗A(3)…⊗A(n)为完全一致性矩阵.

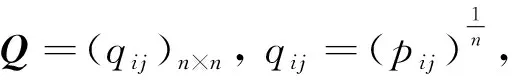
由于人为判断的主观性和片面性，所构造的成对比较矩阵不一定是完全一致的，所以需要进行一致性检验，检验不一致是否在容许的范围内.由定理2知，Q是完全一致性矩阵，即qij=qik·qkj，则不需要进行一致性检验.由完全一致性矩阵性质可知，Q的唯一非零特征根为n，Q的任一列向量都是对应于特征根n的特征向量，可以用其归一化的特征向量作为其权向量.

2 学生遴选授课教师评价体系

2.1 调研过程

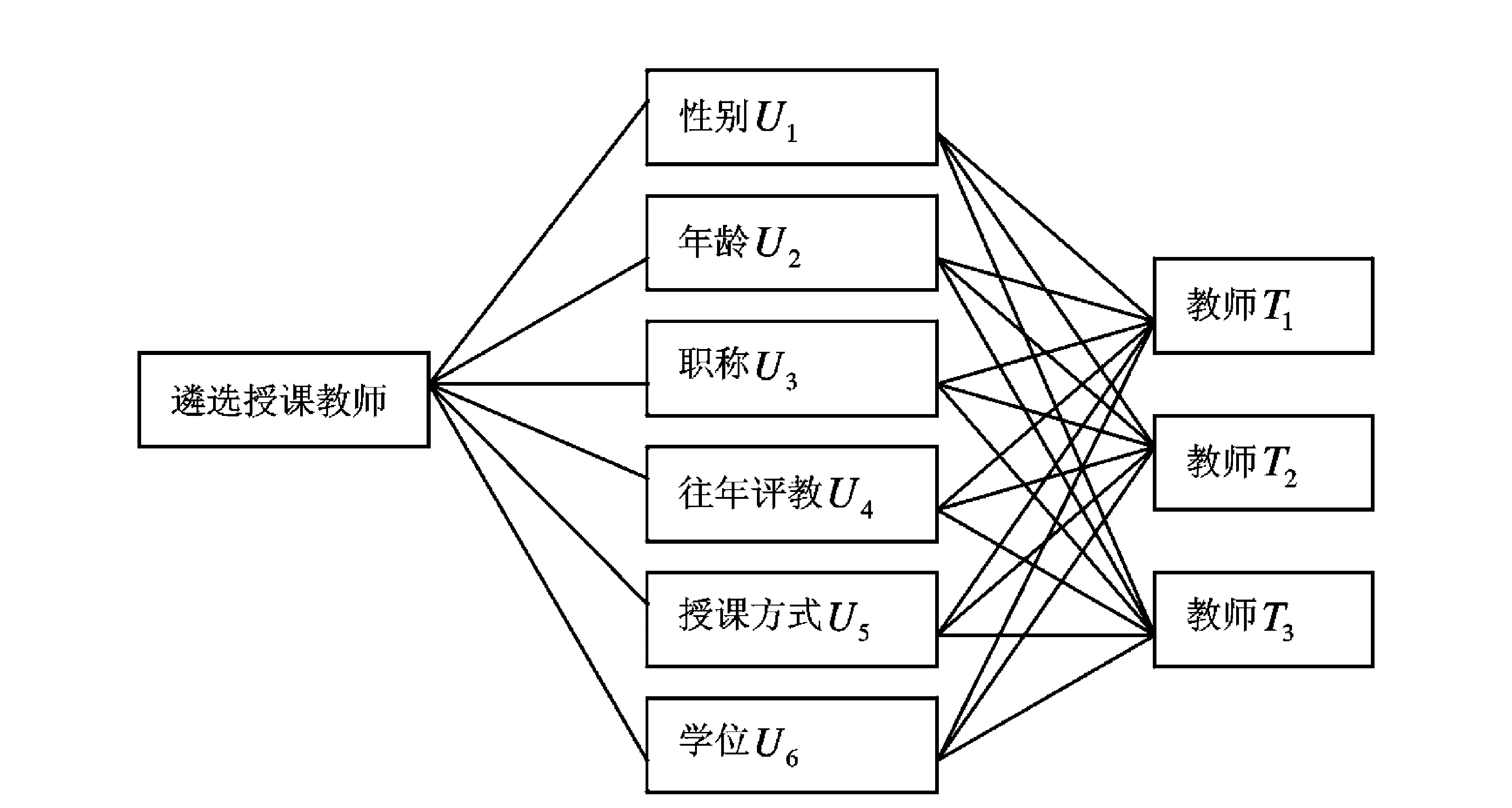
图1 授课教师评价层次结构模型

为得到较为科学、实用的拟授课教师评价体系，本研究参考相关文献并设计调查问卷，问卷涉及拟授课教师的各方面信息，如性别、年龄、学位、工作经历、受教育经历、授课经历、职称、科研水平、拟授课方式、往年的评教结果等，要求被调查者选出认为影响自己遴选授课教师的主要因素，并采用9标度法要求比较各指标之间的相对重要性.以郑州航空工业管理学院2010级的学生为调查对象，从全校46个本科专业中抽样进行问卷调查.共发放调查问卷400份，由相关辅导员老师在课间随机选取学生展开调查，共收回问卷395份，回收率为98.75%.经过筛选,去掉大多数答案相同的无效问卷，共得到有效问卷370份，有效问卷回收率为92.5%.再对调查结果进行相关性分析，剔除高度相关性指标，确定了较为全面的授课教师评价指标体系，并建立了层次结构模型,见图1.

2.2 评价模型的结构

根据层次分析法的原理，所构造的授课教师评价模型最高层为目标层，即遴选授课教师，中间层为准则层，分别是性别、年龄、职称、往年评教、拟授课方式和学位,其评价因素集为U=(U1，U2，U3，U4，U5，U6).最底层为方案层，即为所要选择的授课教师.需要说明的是，上述的层次结构模型并不是一成不变的，这主要是不同学生对不同课程老师的要求也不一样，所以遴选授课教师的评价层次结构模型可以在实践中进一步完善.

3 简单运用

郑州航空工业管理学院2011-2012学年第二学期拟开设运筹学课程，共有3位老师网上挂牌，这3位老师的基本信息如下：

T1：男，29岁，讲师，往年评教良好，多媒体教学，博士学位；

T2：女，36岁，副教授，往年评教良好，多媒体教学，硕士学位；

T3：男，55岁，教授，往年评教优秀，板书教学，学士学位.

从图1可以看出，拟授课教师的评价指标有很多，这使得其相对重要性(权重)不能仅靠经验获得，而需要借助于科学的方法定量导出，这里来用改进的AHP.

根据问卷调查结果确定准则层对目标层的权重，两两比较给出成对比较矩阵A.

由定义2，对矩阵A进行变换得

由定理1得

规范化向量W(2)=(0.042,0.081,0.242,0.304,0.194,0.137)T.

从W(2)可以看出，影响学生遴选授课教师的因素从高到低依次为授课教师往年的评教结果、职称、授课方式、学位、年龄、性别.

建立Ui→(T1,T2,T3)(i=1,2,3,4,5,6)的成对比较矩阵如下：

按照矩阵A的方法，可以得到B1～B6的规范化向量分别如下(篇幅所限，这里各变换矩阵不再写出，过程略)：

W1(3)=(0.400,0.200,0.400)T,W2(3)=(0.168,0.483,0.349)T,W3(3)=(0.122,0.320,0.558)T,

W4(3)=(0.209,0.264,0.527)T,W5(3)=(0.200,0.200,0.600)T,W6(3)=(0.571,0.286,0.143)T.

则归一化权重向量W如下：

则遴选授课教师时的优先排序为：T3>T2>T1.

4 结论

针对当前学生遴选授课教师评价中的不足，根据问卷调查结果确定授课教师评价体系，建立层次模型，并基于问卷调查结果确定成对比较矩阵，用改进的层次分析法确定各指标层次的权重，计算方法科学简便，减少了一致性检验带来的麻烦，为学生遴选授课教师决策提供了科学依据，决策实例表明了该结果的有效性.该模型若能够与计算机结合，推广到其他评价领域并建立相应的评价系统，可实现评价的信息化处理.

参考文献：

[1]Saaty T L.The Analytic Hierarchy Process[M].New York: Mcgraw-Hill,1980.

[2]骆正清.AHP中不一致性判断矩阵调整的新方法[J].系统工程理论与实践,2004,20(6):84-92.

[3]李鹏.服务质量SERVQUAL评价模型修正与发展[J].统计与决策，2007(21):33-35.

[4]Hisu F L.An application of fuzzy AHP for evaluating course website quality [J].Computers & Education,2010 (54):877-888.

[5]张瑞永，张云.AHP判断矩阵向量的改进最小二乘求解[J].数学实践与认识，2009(39):152-156.

[6]陈伟.一种采用拓广最小二乘法的模糊综合评价方法[J].计算机仿真，2009(2):131-134.

[7]温平川，蔡韵.基于AHP模糊综合评判的产学研合作项目风险评估模型[J].统计与决策，2011(1):57-60.

[8]Li Z.A method for constructing perfectly consistent judgment matrix in AHP[J].郑州大学学报,2008,40(1):40-46.