求解热传导方程的Crank－Nicolson方法

陶燕燕

(青岛科技大学 数理学院，山东 青岛 266061)

0 引言

1 Crank－Nicolson差分格式的构造

给出要解决的问题

方程(1)在(xj，tn+12)处满足关系式

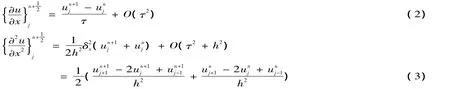
将(2)、(3)式代入(1)舍去误差项得(4)式

上式(4)被称为Crank－Nicolson差分格式，截断误差为O(τ2+h2)

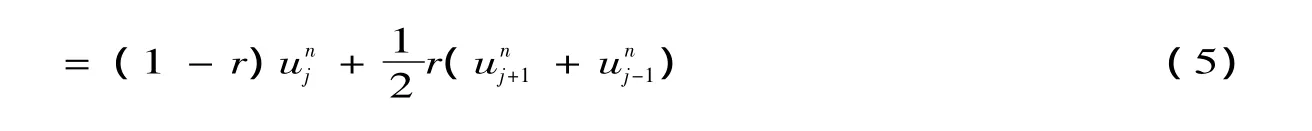
2 Crank－Nicolson格式的稳定性分析

由热传导方程的Crank－Nicolson格式，可将原来方程写为下面的差分方程组:

以下讨论差分方程系数不依赖于时间层面，即Ai=A，Bi=B，故Ci=A－1B=C

上面(6)式可以写为

令 λ1，λ2…λM－1为 C 的特征值，用 ρ(C)表示 λi的最大值，即C的谱半径，则有:

定理1 差分格式(7)稳定的必要条件是，存在与k无关的常数c0，使得矩阵C=A－1B的谱半径满足

证明:因为对于所有的n＞0，有ρn(C)=ρ(Cn)≤Cn

故若差分格式(7)稳定，必有

容易算出(8)式和(9)式是等价的.事实上，若(8)式成立，则有

定理2 若A为正规矩阵，则A2=ρ(A).

定理3［4］若在差分格式(7)中，C=A－1B为正规矩阵，即其满足CC*=C*C，则条件(8)是差分格式(7)按欧几里得范数稳定的充分条件.

证明:当C为正规矩阵时，Cn也是正规矩阵，而正规矩阵的欧几里得范数等于其谱半径，故有Ck2= ρ(Cn)= ρn(C)，因而当(9)式成立时，则

差分格式稳定，又因为式(8)和式(9)是等价的，从而式(8)是差分格式(7)稳定的充分必要条件，证毕.

定解问题(1)的Crank－Nicolson格式是

写成矩阵形式

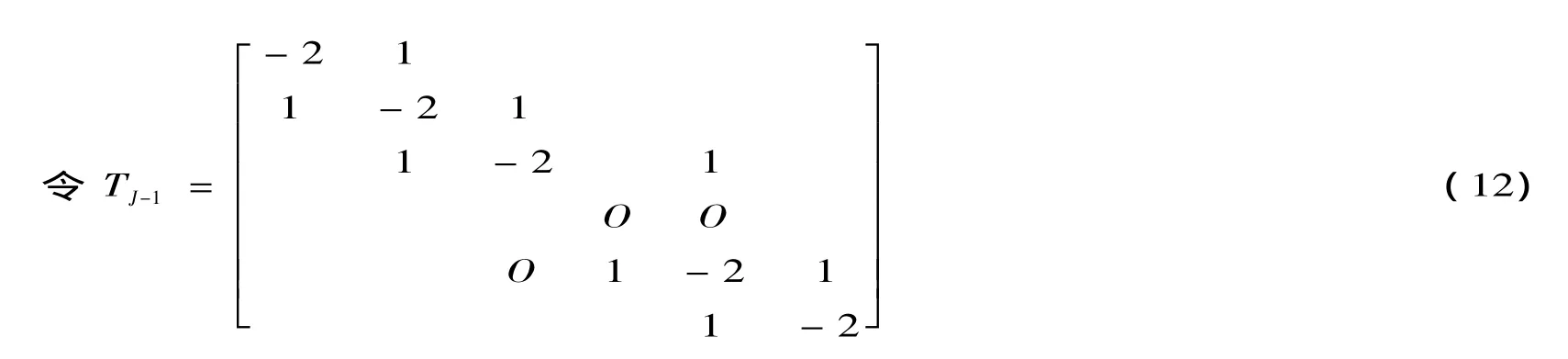
于是 C=(2I － rTJ－1)－1(2I+rTJ－1)

3 数值试验

应用Crank－Nicolson格式计算下列定解问题:

上述定解问题的精确解为u(x，t)=ex+t

表1 部分结点处数值解、精确解和误差的绝对值Table 1 The numerical solutions、the exact solutions and the absolute value of the error in some nodes

表1 部分结点处数值解、精确解和误差的绝对值Table 1 The numerical solutions、the exact solutions and the absolute value of the error in some nodes

n(x，t) 数值解 精确解 |精确解 －数值解|1 (0.5，0.1) 1.822349 1.822119 2.305e －4 2 (0.5，0.2)2.014105 2.013753 3.522e － 4 3 (0.5，0.3)2.225953 2.225541 4.124e － 4 4 (0.5，0.4)2.460072 2.459603 4.692e － 4 5 (0.5，0.5)2.718802 2.718282 5.204e － 4 6 (0.5，0.6)3.004743 3.004166 5.770e － 4 7 (0.5，0.7)3.320755 3.320117 6.379e － 4 8 (0.5，0.8)3.670002 3.669297 7.051e － 4 9 (0.5，0.9)4.055979 4.055200 7.795e － 4 10 (0.5，1.0)4.482550 4.481689 8.612e －4

表2 部分结点处数值解、精确解和误差的绝对值Table 2 The numerical solutions、the exact solutions and the absolute value of the error in some nodes

表2 部分结点处数值解、精确解和误差的绝对值Table 2 The numerical solutions、the exact solutions and the absolute value of the error in some nodes

n (x，t) 数值解 精确解 |数值解 －精确解|10 (0.5，0.1) 1.822121 1.822119 2.281e －6 20 (0.5，0.2)2.013756 2.013753 3.420e － 6 30 (0.5，0.3)2.225545 2.225541 4.115e － 6 40 (0.5，0.4)2.459608 2.459603 4.672e － 6 50 (0.5，0.5)2.718287 2.718282 5.210e － 6 60 (0.5，0.6)3.004172 3.004166 5.776e － 6 70 (0.5，0.7)3.320123 3.320117 6.389e － 6 80 (0.5，0.8)3.669304 3.669297 7.064e － 6 90 (0.5，0.9)4.055208 4.055200 7.808e － 6 100 (0.5，1.0)4.481698 4.481689 8.629e －6

表3 取不同步长时数值解的最大误差Table 3 The maximum error at different step－lengths

［1］李德元，陈光南.抛物型方程差分方法引论［M］.北京:科学出版社，1995.

［2］Dawson C N，Du Qiang，Dupont T.F.A finite difference domain decomposition algorithm for numerical solution of the heat equation［J］.Mathematics of Computation，1991，195(57):63－71.

［3］盛志强，刘兴平，崔霞.对抛物型方程使用新显格式的区域分解算法［J］.数值计算与计算机应用，2005，4:50－253.

［4］戴嘉尊，邱建贤.微分方程数值解法［M］南京:东南大学出版社，2002.