四维动力学模型在高等教育学费问题中的应用

荆禄旭，韩玉群，彭翠英

(青岛科技大学，山东 青岛 266061)

1 引言

高等教育的发展关乎国家的软实力，影响着国家的全局调控，并决定着未来国家的发展.为了能够适应我国经济建设和社会发展的需要，提高全民族的整体素质，满足人民群众接受高等教育的要求，并考虑到我国人口众多的问题，近年来我国加速了高等教育扩招的规模.在满足社会对教育的需求，提高高等学校资源的利用率，提高接受高等教育的人口比例，推动经济多元化发展的同时，也出现了许多被社会所关注的热点问题.例如教育收费与教育公平问题，政府的经费投入与招生规模问题，高校招生规模与毕业生就业问题，大学生失业保险问题，大学生培养质量下降等.解决这些问题已经被提上日程.本文在有关数据的基础上，建立四维微分动力学模型，分析家庭人均收入、政府的生均经费投资标准、高校的招生人数、高校的生均培养费用来确定合适的学费标准.

目前，已经有很多文献介绍了利用数学模型对高等教育规模与教育经费的相关问题的研究，例如，教育经费占国民收入比例－人均国民收入模型［1］，多级模糊评判模型［2］，用SAS软件对教育经费与普通高校招生数进行线性预测［3］，用SPSS软件对教育经费、国民生产总值和高校在校生数三者进行线性预测［4］，高等教育规模波动的政策效应模型［5］等，这些文献中用的方法基本上都是回归统计模型.在文献6中，从就业与招生的关系出发，提出了几个关于高校毕业生就业率和招生规模的微分方程和时滞微分方程模型，给出招生规模、就业率和社会需求之间相协调的定性结论，文献［7］中建立了高校招生规模、政府生均经费与学费标准执教的三维动力学模型，但是却没有考虑影响学费重要部分——家庭人均收入，为此，本文在文献7的基础上，进一步系统的建立高校招生规模、政府生均经费、家庭人均收入与学费标准之间的四维动力学模型，并对行政宏观调控分析.

2 四维微分方程动力学模型

2.1 模型假设与符号说明

首先假设学费标准Y(t)是时间t的函数.影响学费的三个主要指标为高校招生规模、政府生均经费、家庭人均收入，并设家庭人均纯收入、政府的生均经费投资标准、高校的招生人数、高校的生均培养费用，分别用α，β，γ，λ＞0表示;δ＞0为大学生投资成本系数，且大学生投资回报系数成反比.

若设高校的生均培养费用λ.大学生的投资成本系数δ固定为常数，而居民人均纯收入α、政府的生均经费投资标准β与高校的招生人数γ都是时间t的函数.

本文在调查实际情况的前提下做出以下假设:

(1)Y(t)的时间相对变化率与高校的招生人数、居民人均纯收入、政府生均经费投入成正相关，而与生均培养费用成负相关，与大学生的投资成本系数成负相关(不妨先设有关的比例系数为1).

(2)如果学费标准较高(或较低)，就需要政府充分考虑学校的负担能力，通过加大(或减少)相对生均教育经费投入来进行合理的调控.

(3)如果政府生均经费投入较多(或较少)，那么家庭在教育上的支出会减少(或增加)，从而使得家庭人均纯收入相对增加(或降低).

(4)如果家庭人均纯收入较高(或较低)，能够支付高消费用的人数也增加(或减少)，那么高校的招生人数也增加(或减少).

2.2 四维动力学模型的建立

在政府给定高校一个学费基数Ym，家庭人均纯收入有一个标准αm，政府的生均经费投资有一个标准βm，且高校的招生人数在一个标准γm时，根据前面的假设，我们得到如下关于学费标准、高校的招生人数、居民人均纯收入与政府生均经费投入之间的四维微风方程动力学模型:

其中:p，q，l＞ 0为比例系数.

根据Routh－Hurwitz判别准则和稳定性判别法，以及极值分析，有:

定理1:四维微分方程动力学模型(1)在满足条件

时有稳定的平衡点:

证明:由(1)的右端为零，易得(1)的平衡点为(2)，模型(1)在(2)处的线性化系统矩阵如下:

它的特征方程为

由Routh－Hurwitz判别准则，上面方程的所有根具有负实部的必要条件是方程(3)的所有系数全为正，即:

由此可得条件

再根据平衡点的稳定性判别法，我们得到平衡点(2)式稳定的必要条件是(5)成立.

再对模型(1)利用函数极值分析，本文得到高校提高学费收取Y(t)的估计应为:

经过上述分析，我们认为该模型在确定各个假设已知条件的基础上可以给出稳定的学费标注.另外，考虑到各种影响因素之间比例不为1，因此，本文在不影响模型(1)稳定性的前提下，加入正相关系数bi＞0，i=1，2，∧，5，以改进模型如下:

为了确定其相关系数，使用差分模型对未知参数进行求解.模型如下:

通过给定一些数据，可以用上面的差分模型求解出未知参数.然后由上面定理1模型稳定解的分析，本文即可得出国家的学费标准，而各个学校则根据专业不平衡系数和地区发展不平衡系数制定学费标准.据此，本文改进上述模型得到考虑地域和专业的新式模型为:

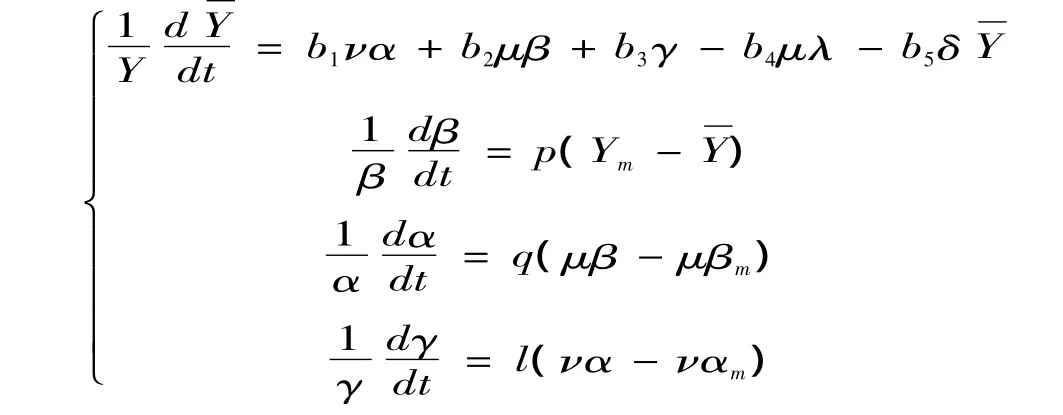
其中，Y为各地区各专业学费，α为家庭人均纯收入，β为政府的生均经费投资，γ为高校的招生人数，λ为高校的生均培养费用，δ为大学生投资成本系数，μ为专业不平衡系数，ν 为地区发展不平衡系数，bi(i=1，2，∧5)，p，q，l为相应比例系数.

3 结论

在本文中，主要得到了下面的几个结果:(1)建立了关于高校招生规模、政府生均经费、家庭人均收入与学费标准之间的四维微分方程动力学模型;(2)给出了模型平衡点的稳定性条件;(3)政府给定高校一个学费基数和高校学费的估计;(4)更加准确的确定了影响高等教育学费的因素，并且对四维动力学模型进行了改进.

［1］靳云汇.教育经费占国民收入比例模型［J］.数量经济技术经济研究，1986，(10):40－44.

［2］段文娟.多级模糊评判模型的高等教育经费支出绩效评价［J］.辽东学院学报，2006，13(3):43－45.

［3］李渺.教育经费与招生数线性预测模型的建立［J］.昌吉学院学报，2003，(2):105－106.

［4］米红，郭书君.未来十年内我国高等教育经费投入状况的理论分析与实证研究［J］.教育与经济，2005，(1):30－34.

［5］黄荣坦，谢作栩.中国高等教育规模波动的政策效应探讨［J］.江西社会科学，2006，(10):28－32.

［6］化存才.高校毕业生就业率和招生规模的数学模型［J］.工程数学学报，2005，22(8):59－62.

［7］化存才.高校招生规模、政府投入和学费标准的三维动力学模型及政府调控［J］.成都理工大学学报(自然科学版)，2007，340(6):657 －660.