具有非齐次定解条件的弦振动方程的解

李同兴

(南京财经大学 应用数学学院， 江苏 南京 210023)

具有非齐次定解条件的弦振动方程的解

李同兴

(南京财经大学 应用数学学院， 江苏 南京 210023)

应用分离变量、叠加原理、齐次化原理和变量替换,讨论了一类具有非齐次初值条件和非齐次边值条件的非齐次弦振动方程解的一般表达式,同时利用傅里叶变换给出了另一种解法.

弦振动方程; 叠加原理; 分离变量法; 齐次化原理; 傅里叶变换

0 引言及预备知识

从物理知识我们知道,一个复杂的振动往往可以分解成许多简单的振动的叠加.如弦振动所发出的声音可以分解成各种不同频率的单音的叠加.而对于每种单音,当弦振动时波形保持不变,于是当时间变化时各点的振幅作同步变化.比如说,每种单音都是具有形式为u(x,t)=X(x)T(t)的特殊解,那么整个复杂振动过程可以通过这种特殊解的叠加得到.

性质3[3]如果f(x),f′(x)都是可以进行傅里叶变换,并且|x|→∞时,f(x)→∞,则有F[f′(x)]=iλF[f(x)].

1 主要结论及证明

对于具有非齐次初值条件和非齐次边值条件的非齐次方程,若φ(x)∈C3,φ(x)∈C2及μ1(t),μ2(t)具有二阶连续导数,且μ1(0)=μ2(0)=0,则利用叠加原理方程

(*)

的求解问题可以分解为求解下列(I),(II),(III)三个方程的通解[4],即:

(1)

(2)

x=0,x=l:u1=0

(3)

(4)

(5)

x=0,x=l:u2=0

(6)

(7)

(8)

x=0:u3=μ1(t)

(9)

x=l:u3=μ2(t)

(10)

引理1 对于形如(I)的弦振动方程,利用分离变量法可得其解的形式为:

证明先求方程(1)的非平凡的特解(即不恒等于零)并要求它满足齐次边界条件(3).利用分离变量法,设解如下:

u1(x,t)=X(x)T(t)

(11)

其中X(x)及T(t)分别表示仅与x有关以及仅与t有关的待定函数.将(11)代入方程(1),得到X(x)T(2)(t)-a2X(2)(x)T(t)=0.将其分离变量,得

(12)

由于在(12)中,左边只是t的函数,右边只是x的函数,左右两端要相等,只有等于同一个常数才行.记这常数为λ(其值待定),就得到

T(2)(t)+λa2T(t)=0

(13)

X(2)(x)+λX(x)=0

(14)

这样,方程(12)就被分离为两个常微分方程,其中一个仅含有自变量t,另一个只含有自变量x,我们可以通过求解这两个方程来解出T(t)及X(x),从而得到(1)的特解(11).

为了使此解是满足齐次边界(3)的非平凡解,就必须找方程(14)得满足边界条件

X(0)=0,X(l)=0

(15)

的非平凡解.由文[5]知方程(14)的通解随λ>0,λ=0,以及λ<0而不同,下面分三种情况讨论:

情况B 当λ=0时,方程(14)的通解可以写成X(x)=C1+C2x.要使其满足边界(15),X(x)也只能等于零.

(16)

将λk代入方程(13)中,可得其通解为

(17)

其中Ak,Bk为任意常数.

因此我们得到方程(1)的满足齐次边界条件(3)的分离变量形式的特解:

接下来利用这种特解的适当的线性组合,求初值问题(I)的解.也即确定Ak,Bk使

(18)

满足初始条件(2).在上述级数两边逐项求导[6]得.

所以由初始条件(2)应有

(19)

将由(19)表示中的Ak,Bk代入(18)式中,就得到用三角级数形式表示的初值问题(I)的解,即解为

引理2 对于形如(II)的弦振动方程,我们利用齐次化原理知其解的形式为:

证明对于(II)由齐次化原理[8]知,若W(x,t;τ)是初值问题

(20)

(21)

由于方程及边界条件都是齐次的,因此方程(21)和混合问题(I)是属于同一类,故可直接利用以上分离变量法得到的结果.再利用(18)和(19)式,我们可以得到:

(22)

引理3 方程(III)的解的形式可以表示为:

且

证明对于方程(III)可设法归结为问题(I)和(II),然后用引理1和引理2求解.为此只需通过未知函数的适当变换把边界条件转化为齐次的即可.令

则它是一个满足边界条件(9)和(10)的函数.再作变换V=u3-U,则它满足非齐次方程和非齐次初始条件:

x=0和x=l时,V=0.

利用叠加原理,这个方程可以分解为如下两个方程:

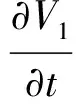
x=0和x=l:V1=0.

x=0和x=l:V2=0.

由引理1和引理2,方程(IV)和(V)的解分别是:

其中

及

及

其中

及

证明利用叠加原理,我们可得该方程的解为u=u1(x,t)+u2(x,t)+u3(x,t),其中u1(x,t),u2(x,t),u3(x,t)分别为方程(I),(II)和(III)的解,然后由引理1～3可以得到的具体表达式.

2 傅里叶变换求解法

我们提供解方程(I)的傅里叶变换方法.在不考虑边界情况下,即方程

(a)

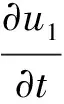
(b)

在方程(a)两边关于x进行傅里叶变换,利用性质1.3,就得到:

最后我们利用傅里叶逆变换得到

由此可见傅里叶变换和逆变换为研究偏微分方程提供了一种思路,并且成为求解偏微分方程的有力的研究工具.

[1] Walter Rudin. Real and Complex Analysis[M]. Third Edition. Beijing: China Machine Press, 2004.

[2] 陈昌平. 数学物理方程[M]. 北京: 高等教育出版社, 1989.

[3] 姜礼尚, 陈亚浙. 数学物理方程讲义[M].3版.北京: 高等教育出版社, 2007.

[4] 郇中丹, 黄海洋. 偏微分方程[M]. 北京: 高等教育出版社, 2004.

[5] 丁同仁, 李承治. 常微分方程教程[M].2版.北京: 高等教育出版社, 2004.

[6] 谷超豪,李大潜. 数学物理方程[M].2版.北京: 高等教育出版社, 2002.

[7] 华东师范大学数学系. 数学分析[M].4版.北京: 高等教育出版社, 2010.

[8] 张恭庆, 林源渠. 泛函分析讲义[M].上册.北京：北京大学出版社, 1987.

[9] 陈祖墀. 偏微分方程[M].2版.合肥:中国科技大学出版社,2002.

[10] Evans L C. Partial Differential Equations[M]. Providence: American Mathematical Society, 1998.

[责任编辑：李春红]

TheSolutionoftheStringVibrationEquationwithInhomogeneousConditionsforDeterminingSolution

LI Tong-xing

(School of Applied Mathematics, Nanjing University of Finance and Economics, Nanjing Jiangsu 210023, China)

In this paper we applied separation of variables, superposition principle, homogenized principle and variable substitution to discuss the general solution expression of a class of vibrating string equations with inhomogeneous initial and boundary conditions, and then we gave another solving method by using the Fourier transform.

string vibration equation; superposition principle; separation of variables homogenized principle; fourier transform.

O175

A

1671-6876(2012)04-0336-06

2012-09-08

李同兴(1987-)， 男， 山东泰安人，硕士研究生， 研究方向为非线性泛函及其应用.