基于密度影响的生态-传染病模型
2012-11-07康爱花
康爱花
(山西大同大学 朔州师范分校 数学系, 山西 朔州 036000)
基于密度影响的生态-传染病模型
康爱花
(山西大同大学 朔州师范分校 数学系, 山西 朔州 036000)
分析并建立了疾病在被捕食者中传播的捕食与被捕食模型,且两种群都受密度制约因素的影响,讨论了系统的有界性和各平衡点存在的条件.首先计算各平衡点对应的雅哥比矩阵,利用Routh-Hurwitz判据分析各平衡点的局部渐进稳定性;其次通过构造Lyapunov函数,由LaSalle不变原理证明了正平衡点的全局渐进稳定性;再次利用比较定理证明了系统的持久性.
模型; 捕食与被捕食; 局部稳定; 全局稳定; 持久性
0 引言
种群动力学主要是解决种群之间相互竞争、互惠、捕食与被捕食关系等,传染病动力学主要研究疾病的传播机理、控制问题等.种群动力学和传染病两方面结合,这样更加符合实际情况,因为种群之间彼此相互依赖,不能完全分开,既考虑种群之间的竞争、互惠和捕食与被捕食的关系,又考虑传染病的传播机理以及控制问题.最近几年对这方面的研究做了不少工作[1].Chattopadhyay[2]针对Salton海中的伽蓝鸟建立了生态-传染病模型,研究了平衡点的存在性及其各平衡点的局部稳定性和全局稳定性.Xiao[3]研究了疾病在被捕食者中传播的捕食与被捕食模型,得到无病平衡点和正平衡点是否稳定的条件,也就是说疾病是否流行的条件,又证明了系统的持久性.Xiao[4]考虑了疾病在捕食者中传播的捕食与被捕食模型,证明了随着传染率的不断增加,正平衡点的变化规律是:稳定—不稳定—稳定.Venturino[5]建立了疾病在被捕食者传播的生态-传染病模型,讨论了各平衡点的存在性、局部稳定性和全局稳定性.但是,大部分模型假设捕食者只捕食染病的食饵,在这里我们考虑疾病在被捕食者流行,且捕食者既捕食染病种群也捕食易感种群,建立模型如下:
(1)
其中,被捕食种群分为易感者种群X1和感染者种群X2,Y表示捕食者种群.r1,r2分别表示食饵和捕食者的内禀增长率,k1,k2分别是食饵和捕食者的密度制约系数,c1,c1分别表示捕食者对易感种群和感染种群的捕食系数,其中e1=μ1c1(0<μ1<1),e2=μ2c2(0<μ2<1),μ1,μ2为转化系数,β表示传染率,α表示感染食饵的死亡率.所有系数都是正数.在此模型中假设感染食饵不再康复,也不能繁殖生育,只影响食饵种群的环境容纳量.
1 预备知识
1.1 有界性

证明定义一函数ω=X1+X2+Y,沿系统(1)对ω求导,可得
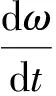
Y(r2-k2Y)-(c1-e1)X1Y-(c2-e2)X2Y≤X1[r1-k1X1]-αX2+Y(r2-k2Y),
对每一个η>0,不等式
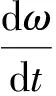
都是成立的.
选取适当的η使0<η<α,则
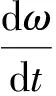
利用常数变易法和比较原理,可得
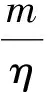
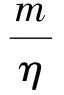
1.2 平衡点存在性
系统(1)有如下非负平衡点:
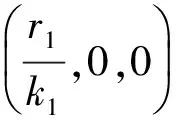
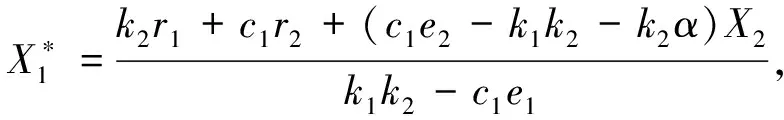
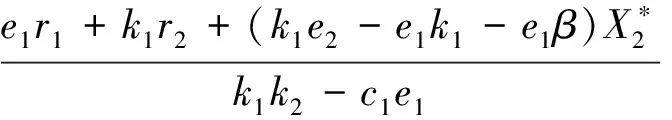
显然, 如果βr1
2 稳定性分析

(2)
将各平衡点代入(2),计算各平衡点的雅哥比矩阵所对应的特征方程的特征值实部的符号,容易知平衡点E0,E1,E3是不稳定的.
当E4不存在时,平衡点E2是局部渐进稳定的.
当βk2r1>βc1r2+c2e1r1+c2k1r2+αk1k2+αe1c1成立时,平衡点E4是局部渐进稳定.显然,当E*存在时,平衡点E4是不稳定的.
对于正平衡点E*的特征方程(2)变为
μ3+Q1μ2+Q2μ+Q3=0,
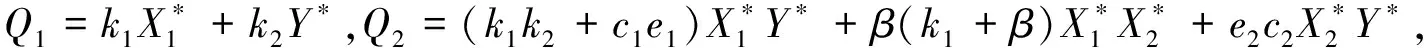

显然,Q1<0,Q3<0,当E*存在时,Q1Q2-Q3<0,根据Routh-Hurwitz判据[6]可知正平衡点E*是局部渐进稳定的.
在此基础上,进一步讨论平衡点E*的全部稳定性.
定理2 在区域D={(X1,X2,Y):X1>0,X2>0,Y>0}上,正平衡点E*是全局渐进稳定的.
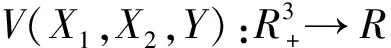
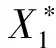
沿系统(1)对V(t)求导,得

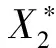
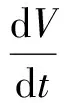
3 持久性

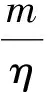
考虑系统(1)的前两个方程,有
(3)
构造比较系统
(4)

4 结论
本文主要讨论了疾病在被捕食者中流行的捕食与被捕食模型,得到了各平衡点存在的条件、局部渐进稳定的条件;通过构造适当的Lyapunov函数证明了正平衡点是全局渐进稳定的,并利用比较定理证明了系统的持久性.
[1] 马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M]. 北京,科学出版社,2004.
[2] J Chattopadhyay, N. Bairag. Pelicans at risk in Salton sea-an eco-epidemiological model[J]. Ecological Modeling, 2001, 136:103-112.
[3] Xiao Y N , Chen L S. Analysis of a three species eco-epidemiological model[J].J Math Anal Appl,2001, 168: 733-754.
[4] Xiao Y N ,Chen L S . A ratio-dependent predator-prey modelwith disease in the prey[J].Appl Math Comput, 2002, 131:397-414.
[5] Venturino E. Epidemics in predator-prey models: disease in the predator[J]. J Math Appl, MedBio,2002,19:185-205.
[6] 马知恩,周义仓. 常微分方程定性和稳定性方法[M]. 北京,科学出版社,2001.
[责任编辑:李春红]
TheDynamicoftheEco-epidemiologicalModelwithDensity-dependent
KANG Ai-hua
(Campus Math Department, Shanxi Shuozhou College, Datong University, Shuozhou Shanxi 036000, China)
In the paper,we analyzed and formulated the prey-predator model with the disease in the prey,considering density-dependent of two species.The boundness of solutions and the existence of the equilibria are studied. First, we calculate the Jacobian matrix,and obtain the sufficient conditions of locally asymptotically stable of the equilibra by the Routh-Hurwitz criterion. Second, we analyze the global stability of the equilibria by using Lyapunov functions and LaSalle invariance principle. At last,the permanence of the system is discussed in term of comparison theorem.
model; prey-predator; locally stability; global stability; permanence
O157.13
A
1671-6876(2012)04-0342-04
2012-09-09
康爱花(1982-), 女, 山西朔州人, 助教, 硕士, 研究方向为应用数学.
