带有推广的反周期边值条件的脉冲分数阶微分方程解的存在性

杨丹丹

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

带有推广的反周期边值条件的脉冲分数阶微分方程解的存在性

杨丹丹

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

研究了带有推广的反周期边值条件的分数阶脉冲微分方程,给出了其解的存在性定理,利用的主要工具是Krasnosel'skii不动点定理.

脉冲分数阶微分方程; Caputo导数; 解的存在性; 不动点

0 引言

本文主要研究以下带有推广的反周期边值条件的脉冲分数阶微分方程:

(1)

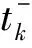
(2)

ay(0)+by(1)=0,ay′(0)+by′(1)=0

(3)

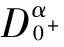
分数阶微分方程的计算理论最早可以追溯到17世纪,它将常微分和积分推广到任意非整数阶.分数阶微分方程在一些数学模型,物理现象分析,化学技术,动力人口学,生物化学,神经网络等很多学科都有广泛的应用.比较经典的有Samko等人[1]与Podlubny的专著[2]和EI-Sayed[3]的文献.近年来,分数阶方程的研究主要集中在边值问题和脉冲边值问题.关于分数阶脉冲微分方程解的存在性,唯一性和解的性质已有较多的成果,成为数学研究者关注的热点[4-6].2012年,Li[7]研究了如下问题:

(4)

Δy(tk)=Ik, Δy′(tk)=Jk,k=1,2,…,m

(5)

ay(0)+by(1)=0,ay′(0)+by′(1)=0

(6)

其中Ik,Jk为常数,a≥b>0.受以上研究论文的启发,本文主要研究问题(1)-(3)解的存在性.我们的主要目的是将线性脉冲边值条件(5)推广到非线性情形(2).需要指出的是本文的主要研究方法不同于已有文献[4-7].

1 预备知识

先给出分数阶微分理论的相关概念[1-3].

定义1 函数u:(0,∞)→R的α分数阶积分定义为

其中α>0,Γ是Gamma函数,并且假设等式右端在(0,∞)上逐点有定义.

定义2 函数u:(0,∞)→R的α分数阶导数定义为

其中α>0,n=[α]+1,并且假设等式右端在(0,∞)上逐点有定义.

定义3 函数u:(0,∞)→R的Caputoα分数阶导数定义为

其中n=[α]+1,并且假设等式右端在(0,∞)上逐点有定义.

接下来,引入本文的一些记号,并给出一个定义.

令AC2[0,1]表示容许函数空间.定义

为问题(1)-(3)的容许函数空间.

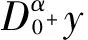
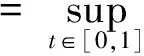
下面,给出本文的主要结果.

2 主要结果

以下列出证明所需要的假设条件:

(H2)Ik,Jk∈C(R),k=1,2,…,m.

(H3) 存在常数Ck>0,Dk>0使得

|Ik(x)-Ik(y)|≤Ck|x-y|,|Jk(x)-Jk(y)|≤Dk|x-y|,

x,y∈R,k=1,2,…,m.

(H4) 存在函数κ1,κ2:[0,1]→[0,∞)且有

(7)

(8)

(9)

使得

|f(t,y)|≤κ1(t)+κ2(t)|y|,t∈[0,1],y∈R

(10)

本文的主要工具是如下的Krasnosel'skii不动点定理.

引理1[8]令M≠φ是Banach空间X一个闭有界凸子集,假设如下条件成立:

(i) 映射A:M→X是全连续的;

(ii) 映射B:M→X是压缩的;

(iii)Au+Bv∈M,对于u,v∈M.

则映射A+B在M中存在一个不动点.

为证明主要结果,需要如下引理.

引理2 若g∈C([0,1],R),则y(t)是如下问题的一个解

(11)

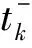
(12)

ay(0)+by(1)=0,ay′(0)+by′(1)=0

(13)

当且仅当

证明由文[7]中引理3.1,容易验证,故在此省略.

令

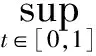
(14)

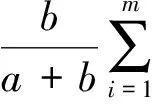
(15)

(16)

定义算子A:M→X和B:M→X如下:

(17)

(18)

定理1 假设(H1)-(H4)均成立. 令L1,μ1≥0,L2>0, 使得L2+η>0,L2+η<1. 则对于r>0满足

L1+(L2+η)r+μ1≤r

(19)

问题(1)-(3)存在一个解满足‖y‖≤r.

证明首先,由Arzela-Ascoli定理,容易验证A:M→X是全连续的.再次,我们证明B:M→X是一个压缩映射.事实上,令u,v∈X,由(H3)和(14),(18),我们有

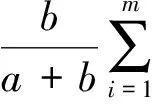
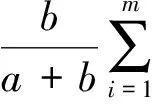
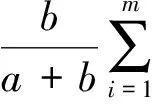
其中η<1.

令u,v∈M,则‖u‖≤r,‖v‖≤r,由条件(H4),(7),(10),(17)式有

由(8)-(10),(15)-(16),对(18)式进行范数估计,有

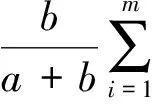
综合以上的范数估计,由(19)式,我们有

‖Au+Bv‖≤‖Au‖+‖Bv‖≤L1+L2r+‖Bv-B0‖+‖B0‖≤L1+L2r+ηr+μ1≤r.

因此,引理1的所有条件都满足,映射A+B在M中存在一个不动点,满足‖y‖≤r.证明完毕.

[1] Samko S G, Kilbas A A, Marichev O I. Fractional Integrals and Derivatives, Theory and Applications[M]. Yveron:Gordon and Breach,1993.

[2] Podlubny I. Fractional Differential Equations[M]. San Diego:Academic Press, 1999.

[3] EI-Sayed A M A. On the fractional differential equations[J]. Appl Math Comput, 1992, 49:205-213.

[4] Wang J, Zhou Y, Feckan M. On recent developments in the theory of boundary value problems for impulsive fractional differential equations[J]. Comput Math Appl, 2012,doi:http://dx.doi.prg/10.1016/k.ca,wa.2011.12.064.

[5] Wang J, Feckan M, Zhou Y. On the new concept of solutions and existence results for impulsive fractional evolution equations[J]. Dynam Part Differ Equat, 2011, 8:345-361.

[6] Ahmad B, Wang G. Impulsive anti-periodic boundary value problem for nonlinear differential equations of fractional order[J]. Comput Math Appl 2010, 159:1341-1349.

[7] Li X P, Chen F L, Li X Z. Generalized anti-periodic boundary value problems of impulsive fractional differential equations[J].Commun Nonlinear Sci Numer Simult(2012),http:/dx.doi.org/10.1016/j.cnsns.2012.06.014

[8] Krasnosel'skii M A. Some problems in nonlinear analysis[J]. Amer Math Soc Transl Ser, 1958, 2:342-409.

[责任编辑：李春红]

ExistenceofSolutionsforImpulsiveFractionalDifferentialEquationswithGeneralizedanti-periodicBoundaryValueProblems

YANG Dan-dan

(School of Mathematical Science, Huaiyin Normal University, Huaian Jiangsu 223300, China)

This paper mainly deals with the existence of solutions for impulsive fractional differential equations with generalized anti-periodic boundary value problems. Sufficient conditions for the existence of solutions are given. The main tool is based on Krasnosel'skii fixed point Theorem.

impulsive fractional differential equations; caputo derivative; existence of solutions; fixed point

O175

A

1671-6876(2012)04-0331-05

2012-08-12

杨丹丹(1982-), 女, 吉林敦化人, 讲师, 博士, 研究方向为非线性泛函分析及其应用.