基于时域伪谱法的二维光子带隙结构的能带研究

孙慧玲

(淮阴师范学院 人事处, 江苏 淮安 223300)

基于时域伪谱法的二维光子带隙结构的能带研究

孙慧玲

(淮阴师范学院 人事处, 江苏 淮安 223300)

根据Bloth定理推导了伪周期电磁场的麦克斯韦方程,采用时域伪谱(PSTD)法分析二维光子带隙结构(PBG)的能带,对空间的微分进行付里叶变换离散而不作差分近似离散,使空域变换成伪谱域．计算结果与平面波展开法的结论相一致．分析了不同截面形状在不同的典型点阵结构中的物理特性．

二维光子晶体; 能带结构; 时域伪谱法

0 引言

光子晶体是一种介电常数或磁导率(也即折射率)为空间场点的函数并且在空间上为周期性分布的电磁材料体系,其周期结构的大小往往可以与波长相比拟．对于非磁性的光子晶体材料,该材料中介电常数呈周期性分布,可以发现光子在其中的行为和电子在晶体中的行为非常的相似．在光子晶体中,周期性折射率调制的存在导致光子在介质的分界面上发生Bragg共振散射,形成相应的Bloch波和由频率决定的能带结构ω(k)．能带ω(k)之间存在着一些频率间隙,频率处在这一范围的各种极化光子在各个方向上的传播都是被禁止的．光子频率ω和bloch波矢k之间存在的色散关系ω(k),决定着光子晶体的能带间隙(光子禁带),因而是光子晶体最重要的特征．如何准确高效的计算光子带隙结构的能带的显示出了尤为重要[1-5]．

自20世纪八十年代末人们开始关注EBG结构以来,就发展了一些用来研究EBG结构的带阻特性和色散特性的方法,如:平面波展开法(Plane Wave Expansion Method,简称PWM)、转移矩阵法(Transfer Matrix Method,简称TMM)、时域有限差分法(Finite Difference Time Domain,简称FDTD法)、有限元法(FEM)、多散射矩阵法等．本文采用时域伪谱(PSTD)法[6-9],它对空间的微分进行付里叶变换而不作差分近似,使空域变换成伪谱域．由于该方法不受色散条件的限制,使单元网格可选取得比传统的FDTD大,从而减小计算规模;另一方面,PSTD法在划分空间网格时,将其磁场及电场的各个分量都定义在网格的中心点上,差分格式比较简单,适合于建立复杂媒质的统一数学模型．

(a) 方柱实空间 (b) 圆柱实空间 (c) 倒空间及最小布里渊区

1 基本原理

1.1 二维光子晶体的TM模的分析

无源、线性各向同性媒质中的Maxwell方程:

(1)

(2)

如果计算区域空间结构是周期变化的,则电场、磁场也是伪周期的,即有:

(3)

(4)

(5)

(6)

(7)

(8)

(9)

对于TE波有:

(10)

(11)

(12)

1.2 伪谱法计算空间导数

在Fourier PSTD中,电磁场量的空间导数是用三角函数来近似的．考虑这样一个1D函数u(x,t),它在0≤x≤L中是周期性的(L即周期)．若x=L/N为元胞的大小,且xj=jx,j=1,2,…,N-1,那么该函数对空间的导数可一般性地写为:

(13)

其中的Dx算符在伪谱法中写为:

Dx(f(x))=IFFTx(ikxFFTxf(x))

(14)

FFT和IFFT,分别表示正向、反向Fourier变换．在Fourier PSTD中,采用三角函数来近似空间导数:

(15)

(16)

2 数值计算及分析

为验证用PSTD 法分析PBG结构色散特性的可行性及正确性,本文计算了各向同性PBG 结构的色散曲线,其结果与平面波展开法(PWE)有较好的一致性,得出有实用价值的结果(图2～图5)．

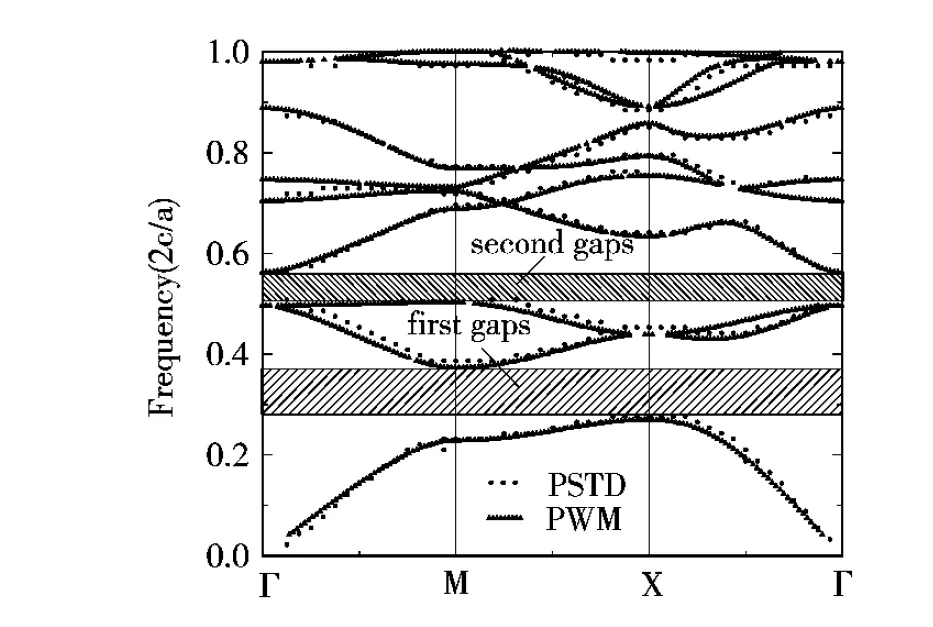
图2 四方点阵中圆柱介质柱的TM波能带曲线图

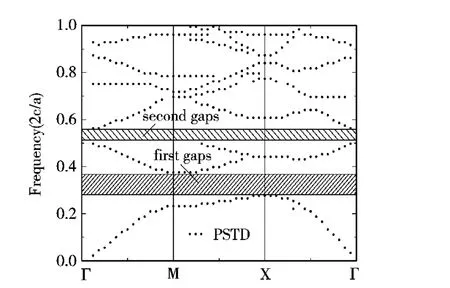
图3 四方点阵中方形介质柱的TM波能带曲线图

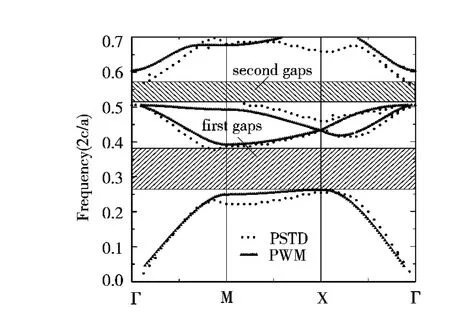
图4 三角点阵中圆形介质柱的TM波能带曲线图

图5 三角点阵中方形介质柱的TM波能带曲线图

算例1 在TM波情形下,二维各向同性电介质柱的PBG结构,晶格常数为12mm,介质圆柱半径为3mm,介质填充比为0.196,介质柱的介电常数为10.2,相对磁导率为1.衬底材料为真空．

算例2 在TM波情形下,二维各向同性电介质柱的PBG结构,晶格常数为12mm,介质方柱边长为5.32mm,介质填充比为0.196,介质柱的介电常数为10.2,相对磁导率为1.衬底材料为真空．

算例1在四方晶格点阵下的计算的能带结构如图2所示,可以看出存在较为明显的两条阻带,分别为频率范围分别为(0.5117～0.5627)(2πc/a)和(0.2804～0.3735)(2πc/a)．与平面波展开法的结果有较好的一致性．证明了本文算法的正确性．

算例1在三角晶格点阵下的计算的能带结构如图3所示,同样看出存在较为明显的两条阻带,分别为频率范围分别为(0.4975～0.5634)(2πc/a)和(0.2779～0.3737)(2πc/a)．

通过图2与图3的比较,我们发现:在四方晶格点阵中,相同的晶格常数及相同介质填充比的条件下,不同截面形状的PBG结构具有十分相近的色散曲线,即介质柱的截面形状对阻带的中心频率及宽度都不敏感．

图4是算例2在四方晶格点阵下的计算的能带结构,可以看出存在较为明显的两条阻带,分别为频率范围分别为(0.2612～0.3767)(2πc/a)和(0.5104～0.5671)(2πc/a),与平面波展开法的结果有较好的一致性．

图5是算例2在三角晶格点阵下的计算的能带结构,同样看出存在较为明显的两条阻带,分别为频率范围分别为(0.2526～0.3615)(2πc/a)和(0.4987～0.5669)(2πc/a)．

通过对图4与图5的比较,我们发现:在三角晶格点阵中,正方形截面形状阻带的中心频率向低频稍稍移动,宽度稍稍变大．比较相同截面不同的晶格点阵可以发现三角晶格点阵中的第一条带隙要比四方晶格点阵中的第一条带隙要略宽．

3 结论

本文采用时域伪谱(PSTD)法,它对空间的微分进行付里叶变换而不作差分近似,使空域变换成伪谱域．该方法不受色散条件的限制,分析二维光子带隙结构的能带计算的有效方法．通过对二维光子带隙结构分析计算,和平面波展开法的结论吻合得较好,证明了本文对基于时域伪谱(PSTD)法的二维磁带隙结构的能带研究的基本原理、主要的数值理论进行研究的正确性．并且分析了不同截面形状在不同的典型晶格点阵结构中的物理特性,为PBG结构的工程设计和应用提供了依据．

[1] Chang C Y, Hsu W C, Photonic Bandgap Dielectric Waveguide Filter[J].IEEE Microwave and Letters,2002,12(4):137-139.

[2] Levy M, Li R, Polarization rotation enhancement and scattering mechanisms in waveguide magnetophotonic crystals[J]. Applied Physics Letters,2006,89:121113.

[3] Liu S, Chen W, Du J, Lin Z, et al. Manipulating Negative-Refractive Behavior with a Magnetic Field[J].Physical Review Letters, 2008,101:157407.

[4] Poo Y, Wu R X, He G H, Chen P, et al. perimental verification of a tunable left-handed material by bias magnetic fields[J]. Applied Physics Letters,2010,96:61902.

[5] Padhi S K, Bialkowski M E.Investigations of an Aperture Coupled Microstrip Yagi Antenna Using PBG Structure[J].IEEE AP-S,2002,3:752-755.

[6] Liu Q H. The PSTD algorithm: A time-domain method requiring only two cells per wavelength[J]. Microwave and Optical Technology Letters, 1997, 15(3):158-165.

[7] 包秀龙, 章文勋, 李乐伟. 各向异性媒质中光子带隙结构色散特性的时域伪谱法分析[J]. 电子学报, 2003, 31(12):1761-1764.

[8] Bao X L, Lin Z F, Sun X W. A new FDTD scheme analysis for the characteristics of the magnetic-anisotropic EBG structure[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2005,15:317-324.

[9] He J P, Shen L F, Zhang Q, et al. A pseudospectral time-domain algorithm for calculating the band structure of a two-dimensional photonic crystal[J]. Chinese Phys Lett, 2002,19: 507-510.

[责任编辑：蒋海龙]

APseudospectralTime-DomainAlgorithmforCalculatingtheBandStructureofTwoDimensionalPhotonicCrystal

SUN Hui-ling

(department of personnel, Huaiyin Normal University, Huaian Jiangsu 223300, China)

In this Letter,we develop Maxwell’s equations of the pseudo-periodic electric and magnetic fields.we calculate the band structure of a two-dimensional(2D) photonic crystal by using the PSTD method. It uses the fast Fourier transform(FFT), instead of finite differences, to represent spatial derivatives. We analyse the physical characteristics in the different cross section shape in different typical lattice structure.

two-dimensional photonic crystals; energy band diagram; pseudospectral time-domain method

O413.1

A

1671-6876(2012)04-0358-04

2012-06-06

孙慧玲 (1981-), 女, 江苏淮安人, 助理研究员, 硕士, 研究方向为电磁场计算、微波电路仿真．