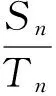与有穷等差数列的中间项有关的竞赛题

●

(吉安师范学校 江西吉安 343000 )

与有穷等差数列的中间项有关的竞赛题

●杨文光

(吉安师范学校 江西吉安 343000 )

若等差数列{an}共有2k-1项，则中间一项为ak；若等差数列{an}共有2k项，则中间2项分别为ak，ak+1．利用有穷等差数列的中间一项或中间2项解题，简捷明快．下面举例说明．

( )

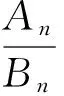
A.2 B.3 C.4 D.5

(2007年湖北省数学高考试题)

(1)

同理可得

B2n-1=(2n-1)bn,

评注an和bn分别为等差数列{an}和{bn}的前2n-1项的中间一项．

例2某等差数列共2n+1项，其中奇数项的和为95，偶数项的和为90，则第n+1项的值等于

( )

A.7 B.5 C.4 D.2

(第十届“希望杯”竞赛试题)

解由a1+a3+a5+…+a2n+1=95，得

即

亦即

(n+1)an+1=95．

同理，由a2+a4+a6+…+a2n=90，可得nan+1=90,从而

an+1=(n+1)an+1-nan+1=95-90=5．

故选B．

评注第n+1项为该等差数列的中间一项．

例3等差数列{an}共有2m+1(m∈N*)项，其中所有奇数项之和为310，所有偶数项之和为300，则m的值为

( )

A.30 B.31 C.60 D.61

(2007年陕西省数学竞赛预赛试题)

解由例2知

(m+1)am+1=310，mam+1=300,

从而

得m=30．故选A．

解易知

a1+a3+a5+…+a2 007=1 004a1 004,

a2+a4+a6+…+a2 008=1 004a1 005，

所以

由式(1)，知

S2 007=2 007a1 004,S2 009=2 009a1 005，

从而

评注a1 004，a1 005为等差数列{an}的前2 008项的中间2项．

例5等差数列{an}中，a5<0，a6>0，且a6>|a5|，Sn是前n项之和，则下列选项正确的是

( )

A．S1，S2，S3均小于0，而S4，S5，…均大于0

B．S1，S2，…，S5均小于0，而S6，S7，…均大于0

C．S1，S2，…，S9均小于0，而S10，S11，…均大于0

D．S1，S2，…，S10均小于0，而S11，S12，…均大于0

(2006年复旦大学自主招生试题)

解由式(1)知

由a5<0,a6>|a5|，知公差d>0，a6>-a5，即a5+a6>0．于是S9<0，S10>0．故选C．

评注a5为等差数列{an}前9项的中间一项，a5，a6为等差数列{an}的前10项的中间2项．另由a1S2>…S5,S5

例6设等差数列{an}满足3a8=5a13，且a1>0，Sn为其前n项之和，则Sn(n∈N*)中最大的是

( )

A.S10B.S11C.S20D.S21

(1995年全国高中数学联赛试题)

解由3(a1+7d)=5(a1+12d)，知

2a1+39d=0.

因为a1>0，所以公差d<0，且(a1+19d)+(a1+20d)=0，即

a20+a21=0,

从而

图1

由二次函数的图像性质(如图1)，知Sn的最大值为S20．故选C．

评注a20,a21，为等差数列{an}的前40项的中间2项，且a20+a21=0．

练习

( )

(第15届“希望杯”全国数学竞赛试题)

(2009年全国高中数学联赛湖北省预赛试题)

3．若{an}是等差数列，首项a1>0，a2 003+a2 004>0，a2 003·a2 004<0，则使前n项和Sn>0成立的最大自然数n是

( )

A.4 005 B.4 006 C.4 007 D.4 008

(2004年重庆市数学高考试题)

参考答案