其实集合试题也可以很精彩——品味近2年高考中的集合试题

●

(湖州中学 浙江湖州 313000)

其实集合试题也可以很精彩
——品味近2年高考中的集合试题

●冯耀斌

(湖州中学 浙江湖州 313000)

集合语言是现代数学的基本语言，是表达数学知识、进行数学交流的重要工具，因此集合知识在高考中倍受青睐，是每年高考中的必考内容．长期以来，不管是学生还是教师，都存在着这样一个误区：高考中集合一般就出现在选择题第一题或者填空题第一题，且都是简单题．而笔者通过分析近2年全国各地数学高考卷发现，其实只要给集合穿件新衣服，集合试题可以很难，当然也很精彩，值得细细品味(限于篇幅，本文仅选取典型的案例进行论述).

1 考查双基，重视基本数学知识

元素与集合的关系和集合的运算是集合知识中最基础的内容，考查此类知识的试题，往往对学生的基本数学思想和方法具有一定的要求,难度不大，只要掌握基本的集合概念、集合运算即可．

例1若集合A={x||x|≤1,x∈R}，B={y|y=x2,x∈R}，则A∩B=

( )

A.{x|-1≤x≤1} B.{x|x≥0}

C.{x|0≤x≤1} D.φ

(2010年江西省数学高考理科试题)

例2已知集合A={(x,y)|x,y为实数，且x2+y2=1},B={(x,y)|x,y为实数，且y=x},且B=A∩B的元素个数为

( )

A.0 B.1 C.2 D.3

(2011年广东省数学高考理科试题)

例1和例2属于基础题，分析略．

答案：C；C．

2 考查思维，注重基本数学思想

求集合的(真)子集个数是历年高考的常见题型．在平时教学时，强调集合A={a1,a2,…,an}有2n个子集，有2n-1个真子集，有2n-1个非空子集，有2n-2个非空真子集.而在实际应用时，往往不会直接套用上述公式，而是需要通过一定的分析，需要基本的数学思想，方能转化为用公式求(真)子集的问题．

( )

A.4 B.3 C.2 D.1

(2010年湖北省数学高考理科试题)

分析本题主要考查集合的子集个数及集合的简单运算．

答案：A．

例4设集合A={1,2,3,4,5,6},B={4,5,6,7,8}，则满足S⊆A且S∩B≠φ的集合S的个数是

( )

A．57 B．56 C．49 D．8

(2011年安徽省数学高考理科试题)

分析本题主要考查集合的关系与运算以及分类讨论思想，题目难度属中等．

答案：B．

3 知识整合，强调综合应用

集合与函数、集合与不等式等内容的碰撞容易产生新的“火花”，题目从形式上看，要比单独函数题、不等式题更加丰富更加饱满．因此，高中数学各个章节内容的整合，不仅仅是知识点的简单复合，更是各种知识体系的交汇，多种解题思想的交融，强调对知识技能的综合应用．

例5设非空集合S={x|m≤x≤l}满足：当x∈S时，有x2∈S．给出以下3个命题：

①若m=1，则S={1}；

其中正确命题的个数是

( )

A．0 B．1 C．2 D．3

(2010年福建省数学高考文科试题)

答案：D．

例6设集合

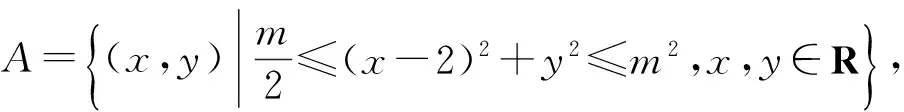
若A∩B≠φ，则实数m的取值范围是________.

(2011年江苏省数学高考试题)

4 挖掘内涵，开阔解题思路

数学试题表面形式可以五花八门，但其本质还是比较明确的．集合的表达形式就有多种，借用集合的“新衣”来装扮的试题种类就更多了：或用集合来表达点、线、面，或用集合来表达数、函数、方程，但究其本质，跳不出“数”和“形”这2个方面.2010年和2011年浙江省数学高考理科的最后一道选择题分别很好地诠释了如何用“形”和“数”的视角来解决集合问题．

例7设a,b,c为实数，

f(x)=(x+a)(x2+bx+c)，

g(x)=(ax+1)(cx2+bx+1)，

记集合

S={x|f(x)=0,x∈R}，T={x|g(x)=0,x∈R}．

若|S|，|T|分别为集合元素S，T的元素个数，则下列结论不可能的是

( )

A.|S|=1且|T|=0

B.|S|=1且|T|=1

C.|S|=2且|T|=2

D.|S|=2且|T|=3

(2011年浙江省数学高考理科试题)

分析本题的内涵是结合集合的知识特别是集合元素个数的新素材考查了函数零点及零点个数的概念，难度较大．

取a=0，b=0,c=0,则

S={x|f(x)=x3=0}，|S|=1，

T={x|g(x)=1=0}，|T|=0，

因此选项A可能成立．

取a=1,b=0，c=1,则

S={x|f(x)=(x+1)(x2+1)=0}，|S|=1，

T={x|g(x)=(x+1)(x2+1)=0}，|T|=1，

因此选项B可能成立．

取a=-1，b=0,c=0,则

S={x|f(x)=(x-1)x2=0}，|S|=2，

T={x|g(x)=(-x+1)(-x2+1)=0}，|T|=2，

因此选项C可能成立．

答案：D．

5 阅读理解，培养信息分析能力

“数学素质是公民文化素质的重要组成部分”．阅读理解能力作为数学素质的有机组成部分，在近几年的全国高考中表现得尤为突出．集合以其特殊的地位成为此类蕴含大量新信息创新题的首选.笔者认为，集合的特殊性由集合论本身的高度抽象、广度范畴，与高中数学集合涉及部分的浅、窄共同作用而形成，以致对集合稍微加点新定义、新知识、新法则，就能在高中数学与高等数学之间的“空白”处绽放出灿烂的光芒．解决这类题目的关键是准确获取新信息，并分析使之转化为与所掌握知识相关联的信息．

例8设S为复数集C的非空子集.若对任意x,y∈S，都有x+y，x-y，xy∈S，则称S为封闭集．下列命题：

①集合S={a+bi|a,b为整数，i为虚数单位}为封闭集；

②若S为封闭集，则一定有0∈S；

③封闭集一定是无限集；

④若S为封闭集，则满足S⊆T⊆C的任意集合也是封闭集.

其中真命题是________(写出所有真命题的序号)

(2010年四川省数学高考理科试题)

分析直接验证可知①正确.

当S为封闭集时，因为x-y∈S，取x=y，得0∈S，②正确.

对于集合S={0}，显然满足所有条件，但S是有限集,③错误.

取S={0}，T={0,1}，满足S⊆T⊆C,但由于0-1=-1∉T，故T不是封闭集，④错误.

答案：①②.

例9设S是整数集Z的非空子集，如果任意a,b∈S，有ab∈S，则称S关于数的乘法是封闭的．若T,V是Z的2个不相交的非空子集，T∪V=Z，且任意a,b,c∈T，有abc∈T；任意x,y,z∈V，有xyz∈V，则下列结论恒成立的是

( )

A.T,V中至少有1个关于乘法是封闭的

B.T,V中至多有1个关于乘法是封闭的

C.T,V中有且只有1个关于乘法是封闭的

D.T,V中每一个关于乘法都是封闭的

(2011年广东省数学高考理科试题)

分析本题考查对新定义集合概念的理解，考查角度新颖，主要考查学生的阅读理解能力和知识迁移能力，难度较大．

答案：A．

6 拓展抽象能力，优化解题策略

提高学生思维能力是国家新课程标准的基本要求，新课程标准重视培养学生的思想品质．因此近2年高考试题构思巧妙，设计新颖，目的是增大考生的抽象思维空间、归纳思维品质及优化解题策略，试题稳中有变、变中求新，始终体现对学生数学解题能力和素养的考查．下面2个例题以集合题目为载体，颇具代表性，高度抽象，同时知识迁移后对解题策略的选择有一定的指导价值．

例10若规定E={a1，a2，…，a10}的子集{ak1，ak2，…，akn}为E的第k个子集，其中k=2k1-1+2k2-1+…+2kn-1，则

(1){a1,a3}是E的第________个子集；

(2)E的第211个子集是________．

(2010年湖南省数学高考文科试题)

分析(1)由所给的定义知

k=21-1+23-1=5．

(2)方法1由题意要使得

k=211=2i1-1+2i2-1+…+2in-1，

可由211=128+64+16+2+1，然后求出相应的i1,i2,…，in．

方法2换种解题策略，此题本质是一个二进制问题，将211化为二进制数是11 010 011(2)，即

11 010 011(2)=27+26+24+21+20，

容易得到i1,i2,…,i5(i1

本题是抽象型新定义试题，构思新颖，亮点明确，主要考查学生在新情境下抽象分析问题、解决问题的能力．

( )

(2011年四川省数学高考理科试题)

分析本题除综合考查了平面向量的数量积、平面向量的应用、排列组合知识之外，还考查了学生应用新知识抽象分析问题、解决问题的能力及逻辑思维能力，难度较大．

答案：B.

以上笔者通过近2年全国各地高考中集合试题出现的频率及不同形式，以“集合”为点，阐述了同一章节内容通过不同知识的包装、不同技能的拓展、不同思维的碰撞后，所产生的多样性和复杂性．因此数学教学的根本任务，是要引导学生建构良好的数学认知结构，以满足其后续学习的需要；教学过程应该重视对数学思想、方法的归纳提炼，认识和把握最本质的因素．