真正的反思是无痕的投入——记一道题目的反思历程

●

(绍兴市高级中学 浙江绍兴 312000)

真正的反思是无痕的投入
——记一道题目的反思历程

●刘海亚

(绍兴市高级中学 浙江绍兴 312000)

新课程实施以来，很多教师对解题的方法和方式进行了反思，笔者认为这些反思大都从数学的角度或者方法的角度进行，它依然带着程序的面孔，走进它并不容易．特别是对于文科学生,他们喜欢有诗意的东西，不愿意接受说教式的反思.因此，如何和着文科生的思维节拍，达到解答题目和心灵快乐的双重效果，在本届高三文科班的数学教学中，笔者做了一些有益的尝试．

1 出乎意外，它是难题

例1过点F(1，0)的直线l交抛物线C：y2=4x于点A，B，记抛物线C的准线为l，设OA，OB分别交l于点M,N，△AOB与△MON的重心分别为点G,H，求|GH|的最小值．

这是笔者所在学校数学期中考试的一道题目.全校406名学生参加考试，完全做对的只有36人．这些学生都用直线和圆锥曲线方程联立的方法来解，运算熟练者胜．数学教学有时就像练习游泳一样，能游也要游，不能游也要扔下去游，在游泳挣扎中学会游泳的思想在一定程度上还是存在的．但这样的游泳，心理成本和时间成本都太大，很容易让游泳者失去快乐，也难以培养勇者的豪迈．笔者决定顺着学生的心灵节拍，对这个题目进行反思．

2 激发共鸣，整装上路

学生的常规解答如下：

设直线方程为y=k(x-1)，点A,B的坐标分别为(xA，yA)，(xB，yB)，联立y2=4x，得出一元二次方程

k2x2-(2k2+4)x+k2=0，

得

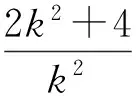
由直线OA，OB的方程分别算出点M,N的纵坐标，然后得出点G,H的坐标(xG，yG)，(xH，yH),其中

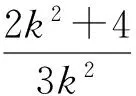
从而

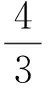
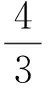
师：下面就考试出现问题的情况作一下“焦点访谈”，请你用最真实的语言陈述，感谢你对数学的诚恳．

(教师就3类典型的解答作现场访谈．)

生1：直线和圆锥曲线联立，思想方法简单但运算不简单，我不喜欢这样的死板，在平时也没有投入过，想想考试的时候练一次就够了，但考试时就无所适从了．

师：感谢你的真实，心不顺则行不从，这个同学坚持内心的做法值得支持，但题目到底是怎么死板的，这值得思考．

生2：我觉得吧，直线和圆锥曲线这种模式要会用，所以在考试的时候照流程下来，但又很不自信，一方面怕投入了很多还是得零分，另一方面又放弃不了这个题．很多步骤上要犹豫，很费时间．最后心就乱了，做了一部分就放弃了．

师：这个同学说的是没有跟这个题目“交心”，什么样的“交心经历”才能对自己放心呢？

师：本次考试还是有很多同学很勇敢，算的时候是“豁出去”的，打算一条道算到黑，运算了这么久，都希望自己的答案是正确的对么？那怎样可以降低答案的错误率呢？

(学生思考.)

生4：老师，点G，H的纵坐标是一致的，线段GH的长度就由它们的横坐标差决定，而点G的横坐标为定值，因此只要点H的横坐标最小就可以了，点H的横坐标取决于xA+xB.由图像可知过焦点的直线在旋转过程中,点F右侧的线段总比点F左侧的线段长，从而线段AB的中点必在点F的右侧.只有当直线垂直时，即中点在点F处时，点H的横坐标最小，此时y轴把矩形ABMN对分成两半，因此答案是-2xH.

学生们的心情逐渐明亮，题目总是没有他们想象中那么“死板”，他们渐渐地安静下来，有的在消化别人的理解，有的在寻找新的发现……

师：刚才我们利用直线和抛物线的位置关系来求解，从解答中能看出这个题目有什么特别的地方吗？

生4：老师，我觉得这里点G，H的纵坐标是一致的比较特别，但我不知道是什么原因？

生5：老师，我觉得直线方程可以设为x=my+1，因为这个方程包含了所有符合条件的直线，这样可以防止忘记讨论直线的斜率问题.

学生5在实物投影仪下呈现他的解法：

设x=my+1，y2=4x，联立方程得

y2-4my-4=0，

从而

yA+yB=4m，yAyB=-4.

由直线OA，OB的方程分别算出点M,N的纵坐标为

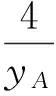
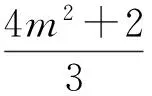
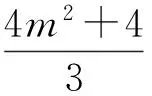
学生开始热闹起来，在接受了第一种解法后还发现有更好的解法，他们开始觉得自己在考试时高估了题目的“威力”.

3 品味题性，别有题天

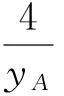
师：很好！这位同学利用yAyB=-4有了惊人的发现，这太美妙了，我们把图像画出来(如图1)．因此形式复杂的数学问题其实是很美丽而富有诗意的，就看你有没有水平领它们出来展示给我们看了．

教师进一步提问是什么原因使得yAyB=-4，学生说过x轴的定点(1，0)，在获得一元二次方程时目测就能看到直线方程中的常数1被保留下来了．

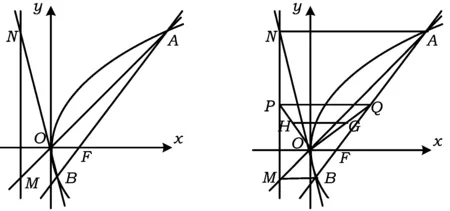
图1 图2

师：如果直线过点(2，0)，那垂线要怎样能够得到yM=yB，yN=yA呢?

生6：现在yAyB=-8，直线方程不变，因此取x=2就能得yM=yB．

师：你能推广到一般情况吗？

生6：假设直线l过点(a,0)，直线x=-a垂直x轴，则直线直线OA，OB与x=-a的交点M,N的纵坐标依然和前面一样．

师：很好!我们把刚才的发现作为AB(学生名字)定理，恭喜你收获数学的巨大发现．

学生们沸腾了，有学生说这种方法也可以证明AB定理，看来几何的直观非常受学生欢迎．

师：很好!这个同学为我们带来了运算便利，大家感谢你．现在我们请他来讲述一下最简单的运算过程．

(学生很自豪，不再赘述.)

从学生轻松愉悦的表达中，笔者知道他们已经懂了．这节课下来，笔者也很开心，上课之前的忧郁少了，课中的开心多了，课后的信心满了，在不知不觉中，对于实践开放式思维，笔者已经从需要自己打气的勇士走向一个自然的镇守者了．

4 不曾预约，美丽翩至

课后有个学生问：“老师，课上我们推广到了AB定理，您看我能不能把这个定理推广到y2=2px?”笔者意识到学生的心被数学打动了，马上回答：“你想到这么好的问题多不容易啊，要是被我解决了太可惜了，要不把自己的想法验证一下，有结果了我来鉴定，如果你连结果也鉴定了，那就告诉我一声．”过了半天，这个学生迫不及待地带着问题和解答来找笔者.

问题过点E(a,0)的直线l交抛物线C:y2=2px于点A,B，设OA,OB分别交x=-a于点M,N，△AOB与△MON的重心分别为点G,H，求|GH|的最小值．

解设直线方程为x=my+a(a>0)，与y2=2px联立得

y2-2pmy-2pa=0,

从而

令x=-a，则

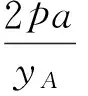
同理可得

yN=yA.

故

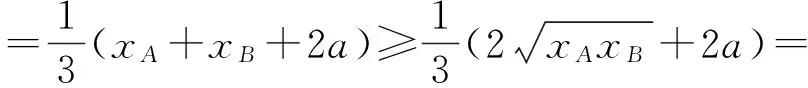
当且仅当xA=xB时，|GH|取得最小值.

新问题：为什么最小值会与p无关呢？

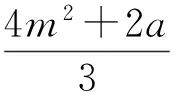
消去m，得到

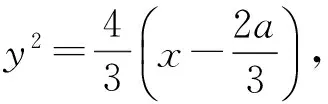
5 兴奋过后，思考感悟

在这节课中，学生的发展高度是教师不曾预设的．以前教师的感受是学生在一定程度上还存在的“刺激—反应”式解题的麻木和顺从，没有思维活力的他们缺乏创造力，也带给教师心灵的疲惫．庆幸的是在教师的引导下，教师和学生的心灵感受对接，和学生的经验对接，对低水平的学生学会倾听他们的感觉，然后一步步告诉学生该如何去发现这种感觉的逻辑指示是什么.“难”意味着要品味题目的个性，“繁”暗示着寻求别的方向或者视角，新的疑问意味着原问题的解决高度有保障．新的视角又带来新的个性解读，带来新层面的疑问解答，反思的不仅是题目，而是该题目隐藏的知识能力系统．学生也想不到自己的不良感受会有这么多的出路，下意识地投入自我对话中，思维品质便自然提升．对涌现过程中的高水平学生，教师要求他们与教师的研究经验对接，品味什么是好问题，品味如何把握兴奋带来的压力，把逻辑思维进行下去．再看这些学生的体验对周围学生的触动，从一下课就熬不住想研究到写条告诉自己如何规划时间研究，再到展示研究成果，学生们感受着激动、成就和成长，这种同伴的自我效能启示对一个班级的影响力是巨大的！

同时，教师自己也很幸福．对于这样一个题目，教师心中有许多的结论，但从学生的视角看到了如此生动的风景，这种风景会滋养一个教师的淡定与高远，修炼自然顺应学生心理的能力，让他们无痕地投入解题和反思，收获一个知识、能力及情感的三维系统．

(本文系2011年绍兴市教改项目：“逾越文科生圆锥曲线教学困难现状的策略研究”的研究成果)

[1] 章建跃．做题目，为什么?[J].中小学数学：高中版，2011(6)：50.

[2] 余文森．有效教学十讲[M].上海：华东师范大学出版社，2009.