“与抛物线有关的定点问题”课例与点评

●

(乐清中学 浙江乐清 325600)

“与抛物线有关的定点问题”课例与点评

●施克满

(乐清中学 浙江乐清 325600)

在新课程标准下，什么样的数学课堂才是高效的数学课堂？高中数学复习课应该怎样体现有效性？适逢温州市马玉斌名师工作室在我校举行教学展示活动，我校高二数学刚好上到圆锥曲线的抛物线部分，于是笔者决定上一节关于抛物线复习的小专题公开课，选定的课题是“与抛物线有关的定点问题”.工作室全体成员对本节课做了精彩的点评，使笔者获益良多，现整理如下与同仁分享.

1 课例

1.1 问题呈现，特殊猜想

问题已知抛物线y2=2x上2个不同的点A(x1,y1)，B(x2,y2),O为原点，满足OA⊥OB，试问：直线AB是否经过定点？若是，求出定点坐标；若不是，请说明理由.

(学生在5分钟内独立思考、自我完成，之后进行小组讨论交流各自的想法.)

教师：很好，对一般问题的思考可以先从特殊情况入手，进行合理地猜想，然后得到结果.现在，我们通过几何画板来检验这个猜想是否正确.

(教师演示几何画板，学生观察图像的变化，发现的确是过定点(2，0)的.)

1.2 4种方法论证，归纳问题本质

教师：尽管特殊法得到的结论是正确的，但是数学的问题是需要严格论证的，哪组同学有办法进行证明？

生B：(解法1)先设直线的方程为

x=my+t(t≠0)，

然后将直线的方程代入y2=2x得到

y2-2my-2t=0，

于是

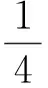
由OA⊥OB得

x1x2+y1y2=t2-2t=0，

得到t=2(t=0舍去).因此直线AB的方程变为x=my+2，过定点(2,0).

(教师板书解答过程.)

教师：生B的解答一气呵成.在解答中，我们看到选择直线方程时，生B设的是x=my+t(t≠0)，与习惯上设y=kx+b不同，能解析一下吗？

生B：设x=my+t(t≠0)，包含了2种情况：当m=0时，x=t表示斜率不存在的直线，当m≠0时，表示斜率存在的直线.而y=kx+b仅表示斜率存在的直线，还要补上斜率不存在的情况.2种做法类似，都可以求解.

教师：生B的分析很有道理，在选择具体的直线方程时，可以根据题目的意思进行灵活的选择.从得到的t=2看，y1y2=-4应该是一个定值，可以验证吗？

(学生思考，讨论，演算.)

生C：还是从问题的条件OA⊥OB入手，我们知道

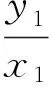
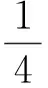
教师：从解法1我们看到了直接设直线AB的方程是可以解决的.其他组有不同的解法吗？

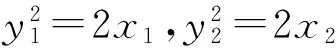
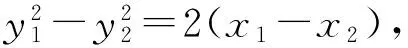
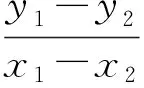
这样直线AB的方程就可以设为

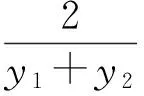
化简得

(y1+y2)y=2x+y1y2=2x-4，

过定点(2,0).

(教师请生D板书解答过程.)

教师：生D也是紧紧围绕直线AB的方程，用y1,y2表示，并且用到了刚才得到的y1y2=-4这一定值，解答过程简洁明了.我们发现这2种解法都是设有多个变量的，生B设x=my+t(t≠0)，生D得到(y1+y2)y=2x+y1y2.能否只用1个变量使问题的解决更明了呢？

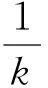
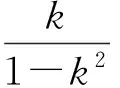
化简得

(1-k2)y=k(x-2)(k≠±1)，

观察发现当k=±1时也满足，因此直线AB的方程为

(1-k2)y=k(x-2),

因此过定点(2，0).

(教师边听边板书解答过程.)

教师：这也是一种常见的解法，将所有的关系用一个变量表示，集中处理，便于发现其中的联系.

(此时，教师发现生F想发言.)

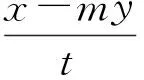
即

ty2+2mxy-2x2=0，

再转化为

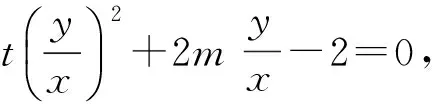
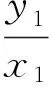
即

t=2.

(教师请生F板书解答过程.)

教师：这种做法实际上就是化为二次齐次方程求解，同时能将原来的问题进行等价处理，需要很强的化归能力.很好！这样我们得到了解决这类过定点问题的几种常见解法，请同学们归纳一下.

生G：解法1:设直线AB方程x=my+t(t≠0)，转化为x=my+2.

解法2:设点A,B的坐标，得到直线AB的方程

(y1+y2)y=2x+y1y2=2x-4.

解法3:设直线OA,OB方程，得到直线AB的方程

(1-k2)y=k(x-2).

解法4:先化为二次齐次方程，然后得到直线AB的方程x=my+2.

教师：从这4种解法中，我们发现最后都是要得到直线AB的方程，并且都是含有参数的.能将这几个式子的特点更一般化吗？

生G：写成B1(x-a)+B2(y-b)=0，其中B1,B2可以是含有变量的值，而a,b是常数，这样就可以得到直线过定点(a,b).

教师：很好.生G通过对这4种解法的分析，得到了一个具有一般意义的式子

B1(x-a)+B2(y-b)=0(a,b是常数).

1.3 一般推广，深化理解

教师：我们知道，数学的很多问题都是可以进行一般化推广的，这样有助于我们对问题的深入理解.现在请大家思考刚才的问题，看看可以在什么情况下进行一般化推广.

生H：可以将y2=2x一般化为y2=2px(p>0).

生I：将OA⊥OB改为kOA·kOB=a(a为常数).

生J：我认为点O也是可以改动的，比如y2=2px(p>0)上的一个定点D(x0,y0).

教师：很好!经过讨论，可以把问题一般化为：

已知抛物线y2=2px(p>0)上2个不同的点A(x1,y1)，B(x2,y2),D(x0,y0)为抛物线上的一个定点，满足kDA·kDB=a(a为常数).试问：直线AB是否经过定点？若是，求出定点坐标；若不是，请说明理由.

现在请大家试试看，能否解决这个一般化的问题？

(学生独立思考、自我解答，小组交流讨论.)

生K：(解法1)设直线AB的方程为

同时由kDA·kDB=a，得

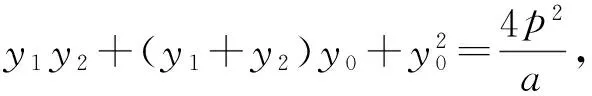
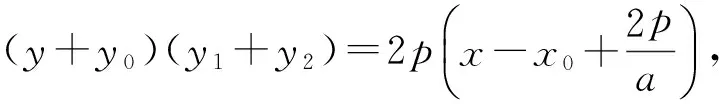
生L：(解法2)设直线AB的方程为x=my+t(t≠0)，代入y2=2px(p>0)得

y2-2pmy-2pt=0，

再将y1+y2=2pm,y1y2=-2pt代入

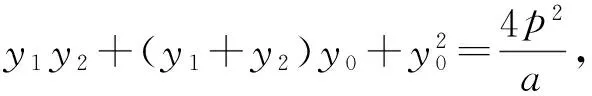
代入直线的方程消去t，得到直线AB的方程为

教师：这是解决定点问题的2种一般方法.通过尝试,我们发现前面采用的设一个变量k的方法和化为二次齐次的方法在这里都存在困难.

1.4 3种变化，凸显本质

教师：从变化的角度上看，对于上面的问题我们仅仅是考察了定点问题的一个类型，即当kDA·kDB=a(a为常数)时的情况.现在进行更广泛的思考，请大家围绕定点产生的条件，即直线必须能化为B1(x-a)+B2(y-b)=0(a,b是常数)这种一般的结构进行思考.

(学生思考、讨论，教师巡视，师生交流.)

生M：(变化1)我们考虑的问题是：

已知抛物线y2=2px(p>0)上2个不同的点A(x1,y1)，B(x2,y2),O为原点，且kOA+kOB=a(a为非零常数).

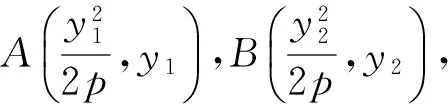
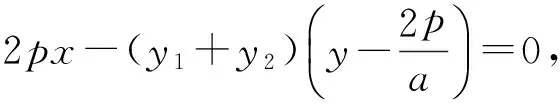
生N：(变化2)我们这样思考：

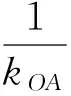
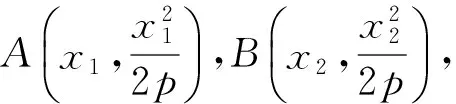
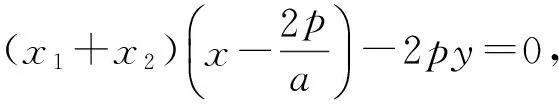
生O：(变化3)我们考虑到当直线OA，OB的倾斜角满足一定关系时也是可以的，正在进行中，结果还没算好.

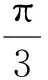
1.5 一般二次曲线的思考(课后继续探究)

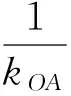
教师：大家的思考非常好，各小组的讨论也很深入，M,N,O这3个小组的同学各给出了一个可行的变化，P小组的同学对今天研究的问题进行了一般化处理，推广到任意的二次曲线，给整节课做了一个小结.希望大家课后继续研究.

2 点评

2.1 选题典型，一题多解，一题多变

这是一节小专题复习课，主要研究与抛物线有关的定点问题.从一个具体问题出发，先考虑特殊情况，得到定点；然后从设点、设直线的方程、设斜率、化为二次齐次式等几个方面进行论证.选择的问题非常典型，学生给出的方法也很有代表性，课堂上注重一题多解，重视培养学生从不同的角度分析和处理问题的能力.

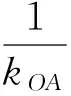
2.2 学生积极参与，问题解决层层递进

新课标指出“必须关注学生的主体参与、师生互动”.本节课教师提供了足够多的机会让不同层次的学生有不同的表现，教师以表扬、赞许等情感语言和鼓掌、微笑、点头等肢体动作，多角度、多方位激励学生，使得原本困难的问题很好地解决，并从多角度对问题进行发散.特别是最后学生小组自我改编问题，从几个不同的角度研究定点问题，将本节课的教学推向高潮，同时教师能将问题的本质在解答过程中给予揭示，有利于问题的解决.教师这样做的目的是培养学生的理性精神和创新意识，为今后的学习和生活播下优质的数学思维种子.

3 自我反思

(1)本节课课堂容量大，需要学生有快速的反应，但是在教学中为了后续问题的展开和深入，常常是看到学生有想法了，就直接请学生回答，使得其他学生没有足够的思考时间.在讲解问题时，没能让学生充分展示解决问题的思维过程，有些可惜.

(2)原来的教学设计中没有解法4(化为二次齐次式)，但是学生提出来而且漂亮地解决了，这是课堂中自然生成的.若教师能够说明怎么样的式子适合二次齐次结构，比如可以举一个例子：已知sin2x-3sinxcosx+1=0，求tanx.可以将式子化为

2sin2x-3sinxcosx+cos2x=0，

这就是一个二次齐次式，再由2tan2x-3tanx+1=0得到tanx.这样学生将更明白这样一种结构.

(3)在问题解决的过程中，请的都是一些有成熟想法的小组，而很多学生没有把错误思维暴露出来，这样就失去了一个纠正错误的机会.其实在教学中更多的是遇到挫折，更重要的是让学生意识到错在何处、如何改正，这样的印象会更加深刻，才会避免错误再次发生.本次课看似非常顺利，但是学生深层次的思维过程没有完全暴露，就使得很多错误的想法被埋没了，这是值得教师重视的.