例析数学知识的深层次理解

●

(三门县教育局教研室 浙江三门 317100)

例析数学知识的深层次理解

●祝敏芝

(三门县教育局教研室 浙江三门 317100)

现今教学实践中，教学模式、教学艺术愈来愈被教师所重视，情境设置可谓创意迭出、精彩纷呈，但很多教师忽视了对数学知识的形成与发展过程、知识之间的相互融合、数学的道理及思想方法的研究，以至于学生掌握的各个知识点相对孤立，整体性不强．无论是数学教学实践还是教学研究，把握数学本质、深层次理解数学知识都是十分重要的．

深层次理解数学知识的涵义是广泛的，至少应该包含以下3个方面：(1)明晰数学知识的背景、形成与发展过程，结合学生的生活经验、数学经验自然合理地诠释新知识；(2)深刻理解数学知识的本质、结构体系，准确地把握数学知识的逻辑意义，感悟数学知识之间的融合；(3)挖掘数学知识蕴涵的思想方法，明晰数学的思维方法、研究方法，体会数学的智慧价值．当然，这三者之间又是相互渗透、密不可分的．

1 明晰数学知识背景，自然合理地诠释新知识

任何数学知识都有一个萌芽、生长、发展的过程．“问渠哪得清如许，为有源头活水来”，要诠释一个新的知识点，首先要明晰知识背景及其发展过程．下面举2个案例：案例1通过知识的横向联系类比提出；案例2通过知识的纵向联系追溯知识的形成背景.

案例1椭圆概念的引入

取一条定长的细绳，把它的两端都固定在图板的同一点处，套上铅笔，拉紧绳子，移动笔尖，这时笔尖(动点)画出的轨迹是一个圆．如果把细绳的两端拉开一段距离，分别固定在图板的两点处，如上操作，画出的轨迹是什么曲线？对比圆的定义作答，在椭圆形成的过程中，哪些量是固定不变的？哪些量是变化的？你能发现动点运动的规律吗？类比圆得到椭圆的实践操作可以让学生感悟到轨迹生成是变与不变的辩证统一．归纳、提升并指导学生课外探究：动点轨迹通常通过定点(定直线)的距离(或其他的几何量)及其四则运算为常数得到．

案例2弧度制的起源与发展

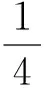
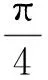
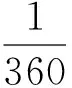
2 理解数学知识的本质及结构体系,感悟知识之间的融合

数学知识的形成与发展有内在的逻辑必然性，知识与知识之间也具有内在的逻辑结构．教师能清楚地指明与某一知识点相关的“知识群”，学生才能把握知识结构的本质，才会形成良好的数学整体观．融合包括初等数学与高等数学的融合、数学各部分的融合、几何观念和算术观念的融合、感性与理性的融合等．如向量的研究就融合了数量、结构及空间这3个数学基本领域．

案例3平面向量的概念及向量方法

“平面向量”第一节课的教学实践往往表现为向量的形式化定义及几个相关概念生涩地堆砌，尤其是单位向量与零向量的引入显得有些苍白、自由向量的描述很不自然．首先，这节课应该让学生懂得认识、研究新对象的基本方法，即从具体背景中抽象出概念的共同特征—定性刻画—定义—定量表示．如表示实数的数轴有3个要素：原点、单位长度、正方向.规定了“单位向量”、“零向量”，才有任意向量的大小表示．“相等向量”的规定表明数学中的向量是与起点位置无关的自由向量．从高等数学“向量空间”的理论结构去理解，相等向量、平行向量是研究等价类的需要，零向量是加法群里的单位元，相反向量是一对逆元．

向量方法的一般步骤是：几何元素—向量表示—向量运算—几何意义．向量及其运算结构充分展示了数量与空间这2个重要领域的完美融合．

例如，用向量方法证明：过一点有且只有一条直线与已知平面垂直．

以已知平面为xOy面建立空间坐标系，在已知平面上取一组基向量e1=(a,b,0),e2=(c,d,0).设n=(x,y,z)为平面的法向量，则

n·e1=0,n·e2=0，

即

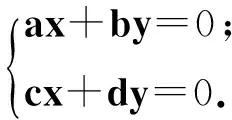
因为ac-bd≠0,所以齐次线性方程组只有零解，即n=(0,0,z)．因此，与平面垂直的方向只有一个，即过一点有且只有一条直线与已知平面垂直．

另外，平面向量的基本定理从数量上精确地诠释了2条相交直线确定一个平面这一平面公理．如果从基本定理的角度去理解空间直线、平面之间的位置关系，会使直观感知与理性思维浑然一体．如线面平行，直线只能与平面内的一个方向平行；线面垂直的直观感知是这条直线与平面内的所有直线垂直，理性思维便是与平面内的2条相交直线垂直．诚然，要确定直线、平面在空间的位置，还需考虑向量的起点．向量是算术观念与几何观念、感性与理性的完美融合．

3 挖掘数学知识蕴涵的思想方法,启迪数学智慧

宏观上的数学思维是一种策略创造，微观上才是严谨的逻辑推理．正如日本数学家米山国藏所说：“在学校所学的数学知识如果不用会很快忘掉，然而唯有铭刻在心中的数学精神、数学思维方法、研究方法和看问题的着眼点，却随时随地发生作用，使他们终生受益．”因此，挖掘数学知识蕴涵的思想方法，并将这些思想贯穿于数学教学的始终，才使学生懂得数学的道理、原理，才能让他们从中获得尽可能多、尽可能大的智慧力量．下文以方程思想中的消元(降维)方法为例，带领读者领略数学思想的强大力量．

案例4等差数列通项公式的推导

方法1a2=a1+d，a3=a2+d=a1+2d，…,an=an-1+d=a1+(n-1)d.

方法2a2=a1+d，a3=a2+d，…，an=an-1+d，将所有式子叠加相消，得到an=a1+(n-1)d．

对于方法1，很多教师仅仅从式子的形式结构上理解，认为是一种不完全的归纳推理，需要用数学归纳法加以证明．方法2通过叠加将a2,a3,…,an-1相消，从而是严密的推理．殊不知，方法1本身就是朴素的、自然的数学归纳法，只不过是用简约的数学符号语言进行了概括.当n=1时是正确的，由n=k时命题的正确性能推出n=k+1时的正确性，那么这个命题是正确的．如果将a1,d,n看作是已知数，那么a2=a1+d,a3=a2+d,…,an=an-1+d实质上是以a2,a3,…,an(即n-1元)为未知数的n-1个一次方程，方法1的推导本质上是代入消元，方法2是加减消元，消去a2,a3,…,an-1，解出an=a1+(n-1)d．从方程思想层面剖析，这个问题是正确的．

案例5简单的线性规划问题

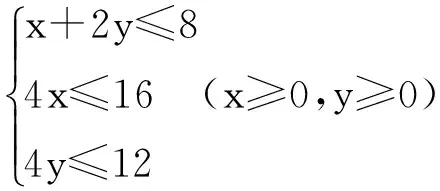
如果我们设计问题：(1)利润有哪些取值,如当(x,y)=(4,0)时,z=8；(2)在平面区域内取哪些值时，z也为8，显然直线2x+3y=8在平面区域内的线段上的任一点对应的z值都相同；(3)取其他点利润又有怎样的分布规律，区域内与直线2x+3y=8平行的任一斜线段上的每一点取到同一个z值，然后分析z值的几何意义．至此，合理自然地将二维的平面区域最值问题转化为一维平行直线系的纵截距的最值问题．这是数形结合的思想方法，但是从根本上看却是“降维”方法，这是通常中的奇巧，平凡中的不凡，可谓“大音希声，大象无形”．

又如空间几何体的三视图，课本上有这样一句话：“我们需要从多个角度进行投影，才能较好地把握几何体的形状、大小．”这句话的表述是不确切的.因为空间几何体上任意一个点的位置由空间直角坐标系中的三维坐标确定，而三视图是几何体在3个坐标平面上的3个正投影，可以确定一个点的三维坐标，所以三视图能精确描述空间几何体的形状与大小．在实际应用中，将三视图作为制作实物模型的图纸，这是三维空间到二维平面的转化．

4 结束语

数学是充满智慧、使人聪明的学科．它在启迪学生智慧方面具有独特的优势和不可推卸的责任．在教学过程中，教师在关注教学方式、教学方法的同时，更要注重数学知识的背景及其逻辑意义，深刻领悟其中所反映的思想方法，挖掘知识所蕴涵的科学方法、理性思维过程和价值观资源．深层次理解数学是艰辛而充满智慧的过程，需要教师有“拨开云雾见月明”的透彻，有“一语天然万古新，豪华洗尽见真淳”的悟性．本文力取弱水三千之一瓢，以期更多的教师“博学之，审问之，慎思之，明辨之，笃行之”．

[1] 克莱因.高观点下的初等数学[M]． 吴大任，舒湘芹，陈义章，译.上海：复旦大学出版社，2008.

[2] 章建跃．中学数学课改的十个论题(续)[J]．中学数学教学参考,2010(4)：2-6．

[3] 李昌官．在读懂数学的基础上教学[J]．数学通报,2011(8)：20-23．

[4] 李袆．学会追问“数学”——数学教师成长的重要阶梯[J]．数学通讯,2011(11)：1-4.