对一道高考调测题几种解法的辨析

●

(上虞市教体局教研室 浙江上虞 312300)

对一道高考调测题几种解法的辨析

●陈尧明

(上虞市教体局教研室 浙江上虞 312300)

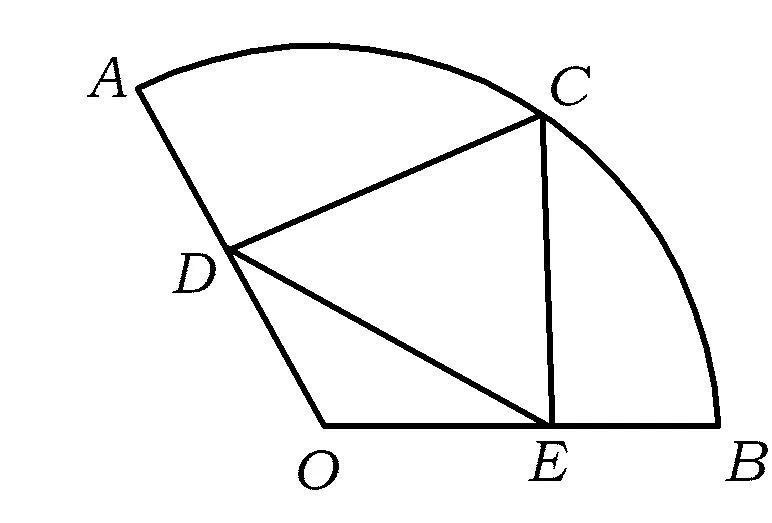
图1

这是2012年浙江省数学高考调测卷(理科)第17题.笔者对学生的答题情况作了统计,从答题情况看,大部分学生能答对取值范围的上限，几乎都错在下限，即最小值求不对；全部答对的学生也很少，正确率很低．笔者对部分学生答题的思维过程进行复原，发现大部分学生是通过取点D(或点E)为特殊位置来蒙的，当然也有极个别学生是利用二次函数根的分布来演绎的．由于是填空题，只知结果不见过程，以致于学生在解题中的一些思维缺陷被掩盖，以下是笔者对解题过程作的辨析．

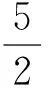
当点E与点B重合,即x=1时，y=0，但此时CD2+CE2+DE2=3，这说明x不可能取到1．于是在式(1)中令y=0得

4x2-2x-1=0，

解得

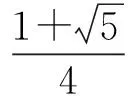
故

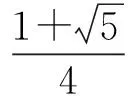
由对称性，不妨令x=y，则

10x2-4x-1=0，

解得

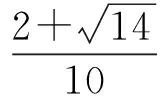
故

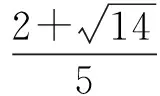
综上所得OD+OE的取值范围是

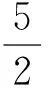
4(x2+y2)-2(x+y)+2xy-1=0，

配方得

4(x+y)2-2(x+y)-1=6xy.

5(x+y)2-4(x+y)-2≤0，

解得

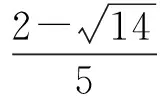
考虑到xy≥0，即

4(x+y)2-2(x+y)-1=6xy≥0,

从而

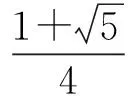
综上可得OD+OE的取值范围是

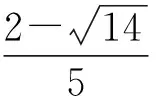
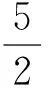
4(x2+y2)-2(x+y)+2xy-1=0.

令x+y=t，则t∈(0,2],将y=t-x代入上式得

6x2-6tx+4t2-2t-1=0.

令f(x)=6x2-6tx+4t2-2t-1，则函数f(x)的零点应在(0,1]内.考虑到

f(1)=4t2-8t+5=4(t-1)2+1>1，

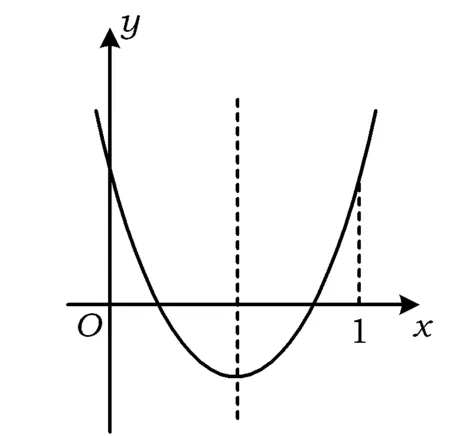
图2

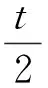
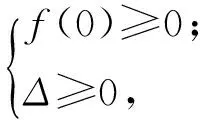
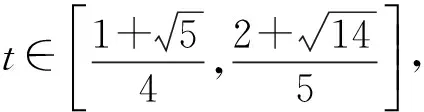
从笔者的调查来看，此题的解法大致是这3种，当然也有部分师生用建坐标系或向量来解，但最终都可以归结到利用余弦定理列出x,y的关系式求解．

由4(x2+y2)-2(x+y)+2xy-1=0得

求导得

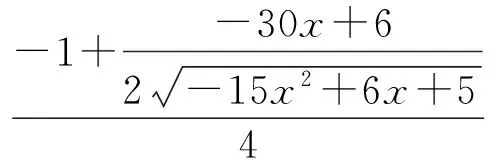
显然y′<0，不妨令y′<-1(注：在一定程度上，当y′=±1时，x与y的变化率是一致的)，即

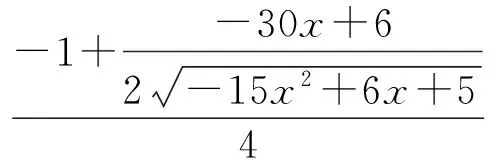
解得

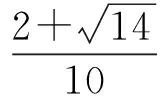
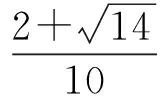
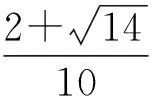
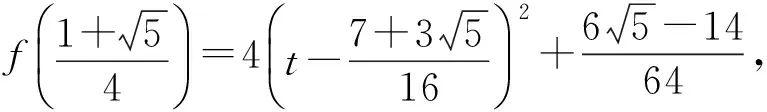
学生丙的结果歪打正着，是正确的．

事实上，可将4(x2+y2)-2(x+y)+2xy-1=0看作是关于x,y的曲线方程，对变量作坐标旋转变换.令

在新坐标系x′O′y′下曲线方程变为

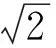
进一步化简得

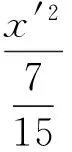
图3 图4

通过以上辨析可以知道，求OD+OE的取值范围，其实是一个线性规划问题，方程4(x2+y2)-2(x+y)+2xy-1=0所确定的曲线图形是椭圆．

再来看2012年浙江省数学高考调测卷(文科)的第17题：

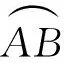
分析由于3条边的平方和改成了2，式(1)就可化为

4(x2+y2)-2(x+y)+2xy=0，

通过坐标变换得