一类二元最值问题的解法探讨

●

(黄陂区第四中学 湖北武汉 430331)

一类二元最值问题的解法探讨

●李红春

(黄陂区第四中学 湖北武汉 430331)

题目若x2+2xy-y2=7(x,y∈R)，求x2+y2的最小值．

这是前不久笔者在高三复习资料上看到的一道试题，给出的已知条件是二次齐次式，既含有交叉项xy，又含平方差的形式，与通常见到的题目不太一样．关于二元的最值问题，通常是借助消元，将二元转化为一元问题来解决.在本题中，用x,y中的任何一个量来表示另一个量都显得很麻烦，因此不少师生对此题一筹莫展.笔者对此题的解法作了一些研究，下面将解法展示给大家，希望能为大家以后解决此类问题提供一些借鉴！

思路1借助第三变量表示，将待求式转化为第三变量的函数.

解法1由x2+2xy-y2=7得

(x+y)2-2y2=7.

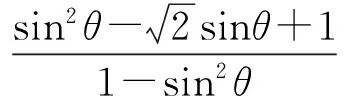
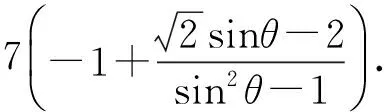
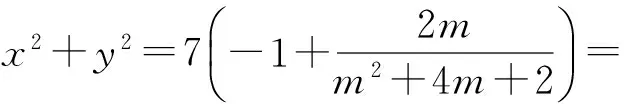
点评此解法源于已知条件左边能写成2个式子的平方差，解答的关键在于由(x+y)2-2y2=7联想到三角平方关系sec2θ-tan2θ=1，进而采用三角换元，将变量x,y统一为θ的函数，解答过程计算量较大．

解法2 设x2+y2=t(t>0)，令x=tcosθ，y=tsinθ，代入x2+2xy-y2=7得

t2(cos2θ-sin2θ)+t2sin2θ=7,

即

t2(cos2θ+sin2θ)=7,

得

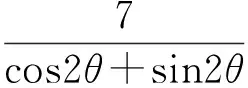
显然

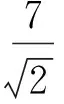
故

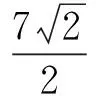
点评和解法1从条件入手不同，解法2则是抓住待求式为平方和这一结构特点采用三角换元，解答简单清晰，让人耳目一新，可谓“此中有真意，欲辩已忘言”！

解法3 由x2+2xy-y2=7得

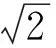
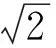
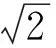
联立求得

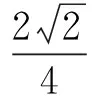
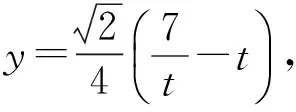
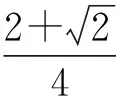
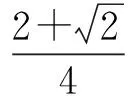
点评解法3的精妙之处在于已知条件能因式分解为2个一次因式的积，采用换元后便能将x,y统一为相同的变量．但若已知条件不能因式分解，解法也就“爱莫能助”了！

解法4 设y=kx，代入x2+2xy-y2=7得

(1+2k-k2)x2=7，

即

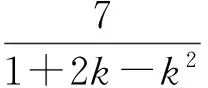
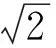
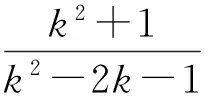
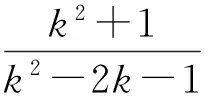
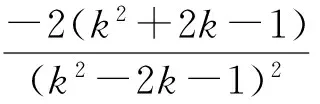
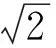
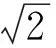
即

点评由于已知条件是齐次式，设y=kx后很容易用k表示x与y，实现双变量的分离，将问题转化为关于k的函数．解法4是解决这类问题的通法，大有“放之四海而皆准”的气魄！

思路2构造含有某个量的一元二次方程，运用判别式法求解.

解法5 设x2+y2=u，则y2=u-x2，代入x2+2xy-y2=7得

2xy=7+u-2x2，

易知x≠0，于是

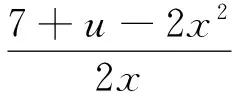
将式(1)代入x2+y2=u，整理可得

于是以x2为未知数的一元二次方程必有正根.由韦达定理知，2个根之和为正，2个根之积也为正，故方程的2个根若存在，则必都为正，当且仅当

Δ=16×(7+2u)2-4×8×(7+u)2≥0，

点评通过换元，巧妙地构造出以x2为未知数的一元二次方程，用判别式法求解，让人有种“曲径通幽处 ，禅房花木深”的意境！

整理得 (7-u)x2+(7+u)y2-2uxy=0.

由x2≠0，得

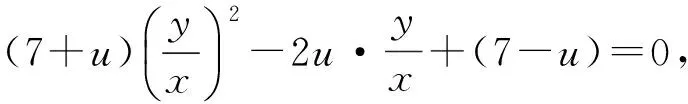
Δ=4u2-4(7+u)(7-u)≥0，

解得

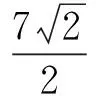
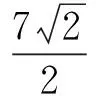
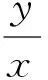
思路3借助不等式相关知识求解.

解法7由题意得

x2+2xy-y2=x(x+y)+y(x-y)=7,

由柯西不等式得

72= [x(x+y)+y(x-y)]2≤

(x2+y2)[(x+y)2+(x-y)2]=

2(x2+y2)2,

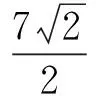
点评对于含有多元的最值问题，运用均值不等式及其变形来求解已很普遍，新教材已将柯西不等式纳入教学的重要内容，大家应努力掌握．解法7的关键在于将已知条件进行恰当的配凑，对学生的能力要求较高，但这正好符合高考“多一点想，少一点算”的要求．

思路4灵活借用其他数学知识求解.

解法8 令z=x+yi，则

z2=x2-y2+2xyi=7-2xy+2xyi,

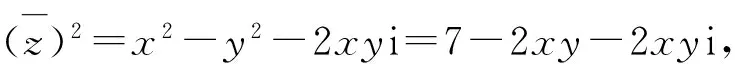
于是

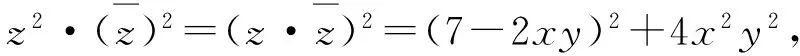
即

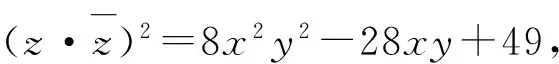
从而

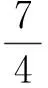
点评待求式x2+y2即为复数z=x+yi的模的平方，而已知条件中-y2=(yi)2，这些都为借助复数解决问题提供了可能．新教材对复数这一章节的内容进行了理性回归，这些都为利用复数工具解决问题提供了更广阔的舞台！

思路5 数形结合求解.

解法9引入新坐标系x′O′y′，设

则x2+y2= (x′cosθ-y′sinθ)2+(x′sinθ+y′cosθ)2=

(x′)2+(y′)2.

由x2+2xy-y2=7得

(x′cosθ-y′sinθ)2+2(x′cosθ-y′sinθ)(x′sinθ+

y′cosθ)-(x′sinθ+y′cosθ)2=7,

整理得

(sin2θ+cos2θ)·(x′)2-(sin2θ+cos2θ)·(y′)2-

2(sin2θ-cos2θ)x′y′=7.

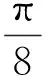
即

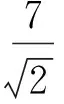
由此可见在新坐标系下该曲线为焦点在x′轴的双曲线，(x′)2+(y′)2表示曲线上的动点到原点距离的平方，由图形可知(x′)2+(y′)2的最小值即为实半轴距离的平方，故

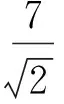
点评数形结合的思想是高中数学中重要的思想.本题待求式x2+y2很容易让人联想到曲线上的动点到原点距离的平方，只是曲线的形状判断要用到坐标旋转等知识，学生只需体会到问题的本质即可．

思路6借助高等数学的知识求解.

解法10令f(x,y)=x2+y2，φ(x,y)=x2+2xy-y2-7，则

L(x,y;λ)=f(x,y)+λφ(x,y)=

x2+y2+λ(x2+2xy-y2-7)，

得

Lx′=2x+λ(2x+2y)=0,

(3)

Ly′=2y+λ(-2y+2x)=0,

(4)

Lλ′=x2-y2+2xy-7=0.

(5)

由式(3)，式(4)消去λ整理得

2xy=x2-y2,

(6)

联立式(4)，式(5)得

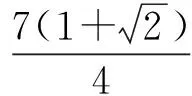
开方后即得稳定点的坐标，故

f(x,y)min=x2+y2=

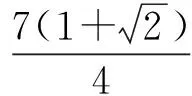
点评解法10需要具备一定的高等数学知识基础，作为学生固然无需掌握.但对于教师，具备一定的高等数学功底和数学素养既有利于理解中学数学问题的来龙去脉，又有助于用高等数学思想、观点、方法解释和理解中学数学中的许多问题．

“一滴水虽小，却能折射出整个太阳的光辉”．本文虽然只就一道二元齐次最值问题的解法进行了探讨，但其中却揭示了解决这类问题的普遍思想方法与技巧，可谓“秀枝一株”，学会了此题，解题中灵活运用便能“嫁接成林”！