例谈课本知识与高考试题的对接

●

(湖州市第五高级中学 浙江湖州 313000)

例谈课本知识与高考试题的对接

●计惠方

(湖州市第五高级中学 浙江湖州 313000)

2010年和2011年的浙江省数学高考文理试卷均将圆作为主角与其他曲线组合入题，形成了一道亮丽的风景.试题不仅形式优美，而且解法多样,是值得研究的好题.下面通过课本知识拓广的实际例子来说明，课本知识与高考试题的对接，希望对高三的针对性复习有一定的启示和帮助.

1 课本习题与高考试题的对接

1.1 圆的直径端点式方程

题目已知圆上一条直径的端点分别是A(x1,y1),B(x2,y2).求证：此圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0.

(人教版高中数学必修2第124页第5题)

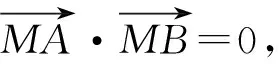
(x-x1)(x-x2)+(y-y1)(y-y2)=0.

1.2 拓广

当点M位置变化时，记以AB为直径的圆为圆N，点M与圆N的关系为:

(1)点M在圆N外当且仅当

(x-x1)(x-x2)+(y-y1)(y-y2)>0；

(2)点M在圆N内当且仅当

(x-x1)(x-x2)+(y-y1)(y-y2)<0.

1.3 应用

(1)当直线l过右焦点F2时，求直线l的方程.

(2)设直线l与椭圆C交于点A，B，△AF1F2,△BF1F2的重心分别为G，H.若原点O在以线段GH为直径的圆内，求实数m的取值范围.

(2010年浙江省数学高考理科试题)

解(1)略.

(2)设A(x1,y1)，B(x2,y2)，联立直线与椭圆方程

由韦达定理知

m2<8.

因为点O在以GH为直径的圆内，所以

解得

m2<4,

从而

m∈(1,2).

小结该题的标准答案有点繁琐，其实条件可减弱为“点G，H分别在射线OA，OB或射线OA，OB的反向延长线上运动(不到达点O)”，结论“原点O在以线段GH为直径的圆内”成立.因此，通过对课本习题的拓广，该问题获得了巧妙的解决方案.

(1)若m=2，求抛物线C的方程；

(2)设直线l与抛物线交于点A，B，过点A，B分别作抛物线C的准线的垂线，垂足为点A1,B1，△AA1F,△BB1F的垂心分别为G，H，求证：对任意非零实数m，抛物线的准线与x轴的交点在以线段GH为直径的圆外.

(2010年浙江省数学高考文科试题)

p=m2=4,

从而

y2=8x.

图1

(2)如图1所示，设A(x1,y1)，B(x2,y2),联立直线与抛物线方程

消去x得

y2-2m3y-m4=0.

由韦达定理知

y1+y2=2m3,y1y2=-m4.

因为m≠0，所以

Δ=4m6+4m4>0.

又因为

x1+x2=m(y1+y2)+m2=2m4+m2,

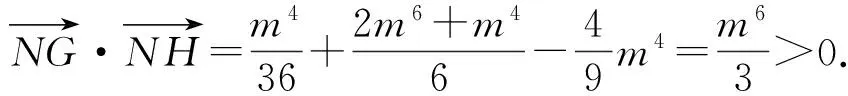
根据拓广的结论知，当m≠0时，点N在以线段GH为直径的圆外.

2 课本概念与高考试题的对接

2.1 直线的两点式方程

2.2 拓广

(y-y1)(x2-x1)=(x-x1)(y2-y1).

(1)

值得一提的是方程(1)表示经过2个点P1(x1,y1),P2(x2,y2)的所有直线(包括x=x1和y=y1).

2.3 应用

例3如图2所示，已知抛物线C1:x2=y，圆C2:x2+(y-4)2=1的圆心为点M.

(1)求点M到抛物线C1的准线的距离.

(2)已知点P是抛物线C1上的一点(异于原点)，过点P作圆C2的2条切线交抛物线C1于点A,B.若过点M，P的直线l垂直于AB，求直线l的方程.

(2011年浙江省数学高考理科试题)

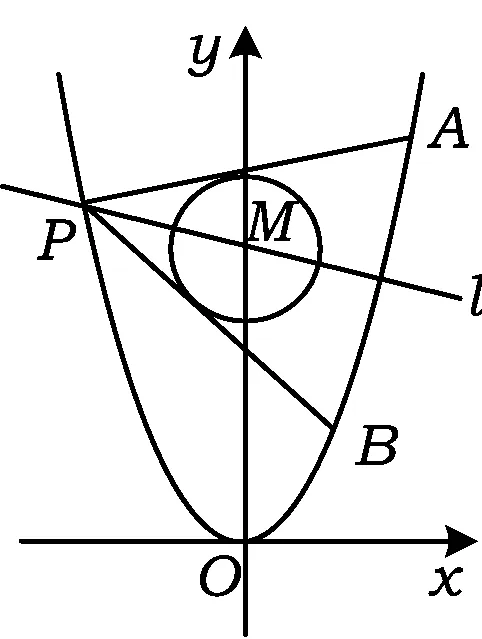
图2

解(1)略.

(m+x0)x-y-mx0=0.

由直线PA与圆M相切知

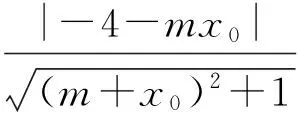
即

同理可得

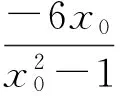
从而

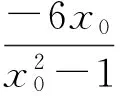
由MP⊥AB知

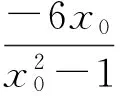
解得

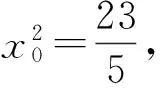
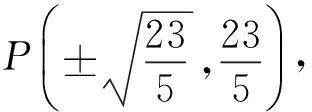
例4如图3所示，设P是抛物线C1:x2=y上的动点，过点P作圆C2:x2+(y+3)2=1的2条切线，交直线l:y=-3于点A，B.

(1)求圆C2的圆心M到抛物线C1的准线的距离.

(2)是否存在点P，使线段AB被抛物线C1在点P处的切线平分？若存在，求出点P的坐标；若不存在，请说明理由.

(2011年浙江省数学高考文科试题)

图3

解与例3的解答类似.

(1)略.

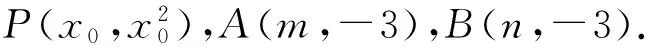
由直线PA与圆M相切知

即

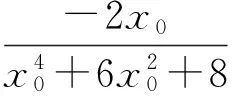
设AB的中点为D，则D的坐标为

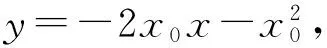
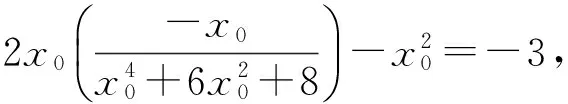
从而

小结例3与例4这2道高考题，标准答案均较繁琐，通过式(1)设直线方程，使解法更简捷，避免了繁冗的讨论.

[1] 计惠方，徐方英.一道浙江高考题的深度解析及纰漏[J].中学数学，2010(5)：56-57.