四法帮你克服思维定势
2012-11-06
●
(金湖县教师进修学校 江苏金湖 211600)
四法帮你克服思维定势
●徐加生
(金湖县教师进修学校 江苏金湖 211600)
思维定势是指一个人用同一种思维方法解决若干问题以后,往往会习惯性地用同样的思维方法解决以后类似的问题,并不关心条件有些许的不同、环境有些许的改变.在数学解题中的表现就是记类型、记方法、套公式,这种思维定势在解决简单的数学题中可能会有一定的效果,不用太多的思考就能解决,但在一些范围广、覆盖面大、具有灵活性的题目中,则会受到限制,因而难以得到较为完善的解题思路和方法,这种现象必须加以克服.本文介绍4种措施,帮你渡过此关.
1 细观察
观察是认识事物最基本的途径,是了解问题、发现问题和解决问题的前提,是数学解题必需的准备阶段.任何一道数学题,都含有题设和结论,只是有些题目条件隐晦或条件与结论混同一体,解题的第一步就是分析题目特征,对题目中的符号、等式、图形及位置关系进行深入、细致、透彻的观察和分析,然后再认真思考.透过表面现象看其本质,这样才能确定解题思路,找到适合自己的、实用有效的解题方法.
例1已知集合M={x|x2-1=0},N={x|ax-1=0},若M∩N=N,则实数a等于
( )
A.1 B.-1
C.1或-1 D.1或-1,或0
分析从已知条件中可以知道,正确理解M∩N=N,即N⊆M是解题的关键,再从各选项去考察,a=1,a=-1都符合题意,主要须考察a=0的情形,当a=0,N=φ,M≠φ,显然有N⊆M,即M∩N=N成立.故选D.
评注本题中,集合M可以化简为{-1,1},而集合N中含字母a,正确地求方程ax-1=0的解就是准确审题的结果,考虑a=0的情形可以从选项中和正确理解N⊆M引发出来,本题的要点是对符号语言M∩N=N的认识和理解.
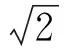
(2009年全国数学高考试题)

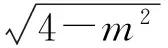
即

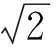
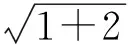
由基本不等式得到

当且仅当m=n时等号成立,即弦AC,BD长度相等时四边形ABCD的面积有最大值为5.
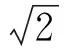
2 用特例
特殊与一般是对立统一的,在数学解题中,一般化是一种常规性的思维方法,而特殊化是一种探求性的思维方法,是一种创造性的思维品质.因此在用常规方法难以破题时,不妨向特殊化考虑,即将问题置于特殊情形、特殊位置、特定图形来思考,或用特殊值、特殊函数、特殊曲线方程进行探求,用简单化、具体化、单一化、边缘化、极限化的手段探索问题的解决途径,注重思考问题在特殊情况下会呈现什么性质或规律,从而激发解题的灵感和智慧.

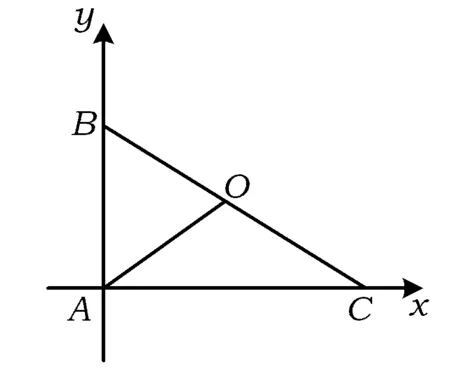
图1

评注本题抓住“直角三角形的外心为斜边的中点”这一重要结论,使求值问题变得简单.由于将三角形特殊化后并没有改变问题的本质,没有使其他的条件变得无效,这是针对本题特征的重要措施.
例4已知a,b,c是实数,函数f(x)=ax2+bx+c,g(x)=ax+b,当-1≤x≤1时,|f(x)|≤1,求证:当-1≤x≤1时,|g(x)|≤2.
分析由于所给函数式含多个参数,直接推理有困难,需用特殊值探查分析,才能得到解题契机.当-1≤x≤1时,有|f(x)|≤1.令x=0,得
|f(0)|=|c|≤1;
令x=±1,得
|f(±1)|=|a±b+c|≤1.
又g(x)=ax+b,则
|g(±1)|= |±a+b|=|a±b|=
|(a±b+c)-c|≤|f(±1)|+|c|≤
1+1=2,
由一次函数图像性质可得|g(x)|≤2.
评注本题抓住函数f(x)与g(x)中的系数a,b特殊关系,利用特殊值探查分析得到|f(±1)|与|g(±1)|的关系,为后面利用不等式|a-b|≤|a|+|b|进行放缩解题创造了条件.
3 勤联想
联想思维是人们在认识事物的过程中,根据事物之间的内在联系,由一事物想到另一相关事物的心理过程.数学联想是探索数学问题解决的触角和向导,是将题目中的已知条件向需求结论转化的桥梁.在解题过程中,通过对题目中已知条件、图形特征以及求解目标的分析研究,联想相关的数学定义、定理、公式、法则,或联想数学各分支中相近的知识与表述以及能反映问题实质的图形(像),运用变通思维、数形转化等方法破解问题.
例5已知定义在R上的函数f(x)是增函数,且f(0)=-1,f(3)=1,则不等式|f(x+1)|<1的解集是________.
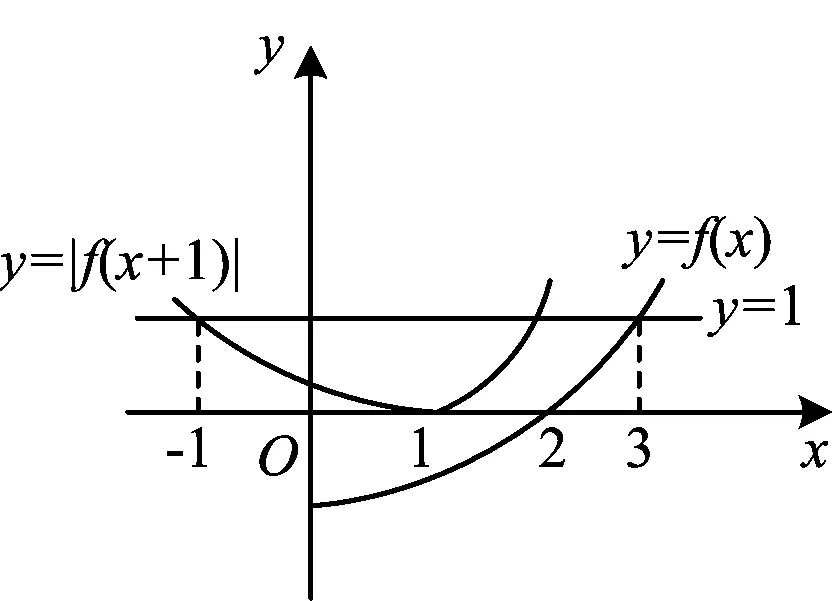
图2
分析由已知的函数定义及所经过的特殊点(0,-1),(3,1)可联想到函数f(x)图像的大致走向,如图2.而f(x+1)是由f(x)向左平移一个单位得到,|f(x+1)|是由f(x+1)把在x轴下方的图像向上翻折得到,那么点(0,-1)变为(-1,1),(3,1)变为(2,1),故要使|f(x+1)|<1,由图像变化可知x∈(-1,2).
评注这是一个与抽象函数有关的解不等式问题,不能直接解不等式,但通过对已知条件的联想分析,转而研究此函数的大致图像达到解题目的.
例6已知a,b是实数,函数f(x)=x3+ax,g(x)=x2+bx,f′(x)和g′(x)分别是f(x)和g(x)的导函数,若f′(x)g′(x)≥0在区间I上恒成立,则称f(x)和g(x)在区间I上单调性一致.
(1)设a>0,若f(x)和g(x)在区间[-1,+∞)上单调性一致,求b的取值范围;
(2)a<0,且a≠b,若f(x)和g(x)在以a,b为端点的开区间上单调性一致,求|a-b|的最大值.
(2011年江苏省数学高考试题)
分析由于f′(x)=3x2+a,g′(x)=2x+b,根据f(x)和g(x)单调性一致的定义知,(3x2+a)(2x+b)≥0在区间(-1,+∞)恒成立,又a>0时,3x2+a>0,即有b≥-2x在[-1,+∞)上恒成立,因此b≥2.

当x∈(-∞,0)时,
g′(x)<0;
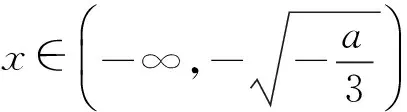
f′(x)>0,
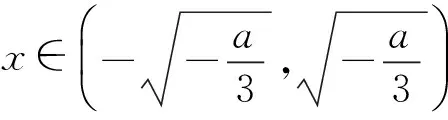
f′(x)<0;
要使f(x)和g(x)在以a,b为端点的开区间上单调性一致,根据定义应有
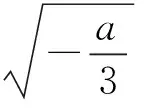

评注本题新定义了2个函数单调性一致的概念,理解和正确应用这一新定义是解题关键,所以解题活动都必须围绕这个中心进行,如在求|a-b|的最大值时,变通思维,运用f′(x)g′(x)≥0恒成立确定a,b的范围,这就抓住了问题的核心,从而明确了解题方向.
4 善转化
由于客观世界在不断运动变化之中,转化是解决问题的永恒主题.数学中的转化思想就是要求我们换一个角度去看、换一种方式去想、换一种语言去讲、换一种观点去分析任何数学问题,使问题朝着有利于解决的方向不断变更、发展.等价转化思想是解决数学问题的重要思想方法,常用方法有:把复杂结构向简单结构转化,把抽象问题向具体问题转化,把未知结论向已知条件转化,把正面叙述向反面表达转化等.
例7已知P是直线3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的2条切线,A,B是切点,C是圆心,那么四边形PABC面积的最小值为________.

评注一些表述复杂或思维层次较多的问题,解决的方法就是一步一步向简单问题转化,把熟悉的简单问题都解决后,再串联起来就容易解题了.


(2011年山东省数学高考试题)
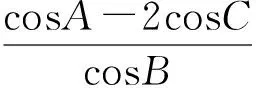
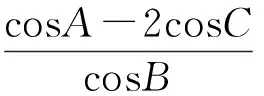
然后去分母化简得
sinBcosA-2cosCsinB=2sinCcosB-sinAcosB,
即 sinAcosB+cosAsinB=2(sinCcosB+cosCsinB),
得
sin(A+B)=2sin(B+C).
又在△ABC中,A+B=π-C,B+C=π-A,故
sinC=2sinA,
即


4=a2+c2-2accosB,
代入解得c2=4,因此c=2,a=1,故△ABC面积

评注通过研读题目可得到如下信息及相关思考:①三角形中的问题,应该想到内角和定理及正、余弦定理;②给出的条件是2边不同结构的比值,消除差异是第一目标.再一个是去分母后式子向什么方向变形,即找到转化的准确目标位置,这需要熟悉正弦的两角和公式等知识点.
由于数学问题的千变万化,要想既快又准地求解问题,就必须破除思维定势,注意问题的变化和方法的变通,让思维动起来,让技巧飞起来,这样我们的能力才能有更大提高.
