简谈2个圆锥曲线的非标准方程

●

(常州高级中学 江苏常州 213003)

简谈2个圆锥曲线的非标准方程

●徐德同

(常州高级中学 江苏常州 213003)

学生对于圆锥曲线的标准方程已非常熟悉，但有一些非标准方程，也常常出现在我们的视野中.如果能够利用适当的变换去化“非标准方程”为“标准方程”，进而辨析它们的类型,认清方程对应的曲线,不仅能打开问题的思路，往往还能减少计算.本文抛砖引玉，主要介绍2种非标准方程及其应用.

1 方程xy=λ(λ≠0)对应的曲线

事实上，只要作一个旋转变换，把坐标轴绕原点顺时针转45°.令

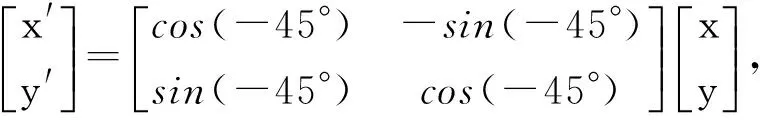
即

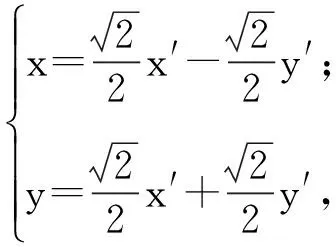
(x′)2-(y′)2=2λ，

(1)

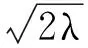
例1如图1所示，设曲线xy=1的2支为C1，C2，点P，Q，R位于曲线上.

(1)如果点P为C1上的动点，试问平面上是否存在2个定点M，N，使||PM|-|PN||的值为常数；

(2)如果点P为C1上的定点，坐标为(-1，-1)，点Q，R在C2上，且△PQR是正三角形，求点Q，R的坐标.

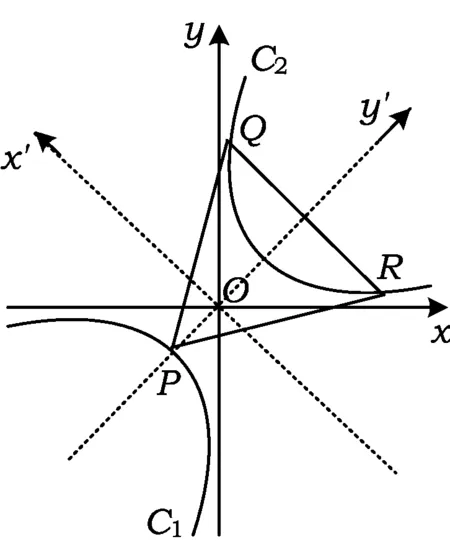
图1

分析在式(1)中，令λ=1，得(x′)2-(y′)2=2，是等轴双曲线.

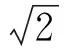
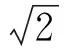
解得

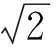
由对称性知

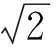
在原坐标系中，不难求得

2 方程x2±xy+y2=λ(λ>0)对应的曲线

作一个旋转变换，把坐标轴绕原点逆时针转45°.令

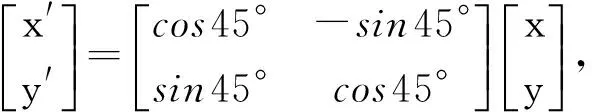
即

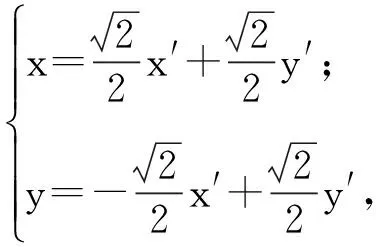
(2)

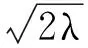
同理可得方程x2-xy+y2=λ(λ>0)对应的曲线是椭圆

(3)

分析在式(2)中，令λ=1，得

令

则

例3已知实数x,y满足x2-xy+y2=3，求x2+xy+y2的取值范围.

(2010年江苏省苏锡常镇数学模拟考试试题)

分析作一个旋转变换，把坐标轴绕原点逆时针转45°.令

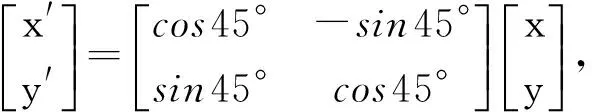
即

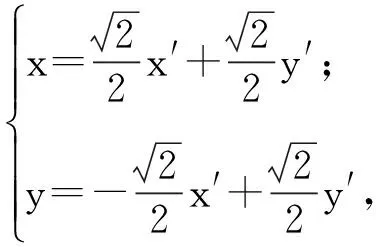
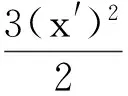
即

则

cos2θ+9sin2θ=8sin2θ+1，

故所求的取值范围是[1,9].