数学解题应强化估算意识
2012-11-06
●
(资阳市外国语实验学校 四川资阳 641300)
数学解题应强化估算意识
●蔡勇全
(资阳市外国语实验学校 四川资阳 641300)
估算,顾名思义,估摸着计算,是以正确的算理和深刻理解研究问题的本质为基础,通过大体估值、合情猜想和特值探路等手段,进行粗略、近似地计算并获得正确答案的过程.在数学解题中渗透估算意识,有效地避免了以往“小题大作、费时费力”的逻辑推理过程,达到了简洁、快速、合理、准确解题的目的,恰到好处地契合了近几年高考命题倡导的“多考点想、少考点算”这一基本理念.本文略举数例介绍估算法在数学解题中的应用,仅供参考.
1 借助局部与整体的关系进行估算
若研究对象是由若干个部分构成的,可先研究其中易求的一个或几个部分,再把所得结果同局部与整体的关系联系起来估算整体的结果.

( )
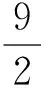
分析直接计算该多面体的体积费时费力,可联结BE,CE,将原多面体的体积转化为四棱锥E-ABCD和三棱锥E-BCF的体积之和.易求VE-ABCD=6,由局部与整体的关系可知原多面体的体积应大于6.故选D.

图1
2 借助极限思想进行估算
例2三棱柱ABC-A1B1C1的所有棱长均为a,且侧面A1B1BA⊥底面A1B1C1,则直线C1B与平面A1B1BA所成角的范围是
( )



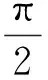
BD=a;
当θ→0时,

从而

因此
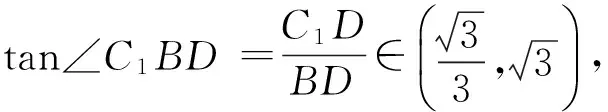
故选B.
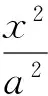
( )
A.60° B.75° C.90° D.120°
分析由选项信息可知∠MFN的大小不会随点P的变化而变化,故当P→B时,点M无限接近于x轴,点N向下运动直至无穷远处,此时∠MFN→90°.故选C.
注极限思想是挖掘几何与分析几何运动问题中某些不变量的有力工具.
3 借助直觉思维进行估算
例4在正方体ABCD-A1B1C1D1中,M为棱DD1的中点,N为棱BC的中点,P为棱A1B1上任意一点,则异面直线AM与PN所成的角等于
( )
A.90° B.60° C.45° D.30°
分析AM为定直线,PN是经过定点N的直线,由于备选答案均是定值,可见AM一定垂直于PN所在的某一个平面,才可能为定值.在这种直觉思维下估算,不难发现,AM⊥平面A1B1N.故选A.
4 借助二项展开式进行估算
当解题过程出现形如(a+b)n(n∈N*,n≥2)的结构而结果又要求保留近似数时,可采用二项展开式适当放缩并大致估值.
例5求0.9986的近似值,使误差小于0.001.
分析0.9986= (1-0.002)6=
1+6×(-0.002)1+15×(-0.002)2+
…+(-0.002)6,
取展开式中第3项
T3=15×(-0.002)2=0.000 06<0.001,
且第3项以后的所有项的绝对值都小于0.001.因此从第3项起,以后的项都可以忽略不计,即
0.9986= (1-0.002)6≈1+6×(-0.002)=
0.998.
注对二项式(1+x)n展开,当x的绝对值与1相比很小且n很大时,含有x2,x3,…,xn的各项的绝对值都很小,在精确度允许的范围内可以忽略不计,因此可用近似计算公式(1+x)n≈1+nx.再如下面一道题:
例6居民收入是由工资性收入和其他收入2个部分组成的.2003年某地居民人均收入为3 150元,其中工资性收入为1 800元,其他收入为1 350元.预计该地区居民自2004年起工资性收入将以每年6%的年增长率增长,其他收入每年增加160元,根据以上数据,2008年该地区居民人均收入介于( )之间
A.(4 200,4 400) B.(4 400,4 600)
C.(4 600,4 800) D.(4 800,5 000)
大夫郑重提醒:因不能面诊患者,无法全面了解病情,所作建议仅供参考,具体诊疗请一定到医院在医生指导下进行。
分析由条件知,该地区居民工资性收入自2003年起构成以a1=1 800为首项,q=1+6%为公比的等比数列.2008年的工资性收入为
a6= 1 800×(1+0.06)5≈
1 800×(1+5×0.06)=2 340.
其他收入构成以1 350为首项,公差为160的等差数列,2008年其他收入为1 350+160×5=2 150元.因此,2008年该地区居民人均收入约为2 340+2 150=4 490元.故选B.
5 借助构造模型进行估算
例7设P为空间中的一点,PA,PB,PC,PD是4条射线.若PA,PB,PC,PD两两所成的角相等,则任意2条射线所成角的余弦值为
( )


注在立体几何中,常构造正四面体模型、正方体模型、长方体模型等进行估算;在函数试题中,常构造一次函数模型、二次函数模型、指(对)数函数模型等进行估算.
6 借助取值范围进行估算

( )


故选D.
例9已知实数a,b,c满足
则实数a的取值范围是
( )
A.RB.a≤1或a≥9
C.0 分析由b2+c2+bc-6a+6=0,得 纵观4个选项,只有D符合要求.故选D. 注借助相关量的取值范围进行估算,简洁明了,操作性强,易于接受. 华罗庚先生曾指出“数缺形时少直观,形少数时难入微;数形结合百般好,隔裂分家万事非”.由此可见数形结合思想在数学中的重要地位,切实把握数形结合思想也是学好数学的关键之一.事实上,借助形数转换进行估算解题有时也能让人眼前一亮. ( ) (2005年湖北省数学高考试题) 特例估算即以特殊估计一般,对一般性问题进行特殊化处理,如选取特殊值、验证备选答案等.特例估算要求根据题意和备选答案,找备选答案之间的区别和联系,有目的地在备选答案中选取一些特殊值、特殊图形、特殊函数、特殊数列或特殊点等进行检验. 例11同例4. 分析由直线AM、点N及AM与PN所成角的确定性和点P的运动性,可考虑用特殊位置法进行估算.取CC1的中点M′,由于AM∥BM′,可平移AM到BM′.当P位于点B1时,联结B1N,易知B1N⊥BM′,从而 PN⊥AM. 故选A. 例12在(0,2π)内,使sinx>cosx成立的x的取值范围为 ( ) 分析考虑用特殊值法进行估算,取x=π,显然满足要求,可排除选项A,B,D.故选C. 例13已知三棱锥P-ABC的侧面与底面所成的二面角均为60°,底面三角形的3条边长分别是7,8,9,则此三棱锥的侧面面积为 ( ) 例14(用计算器探究问题)方程x3+lgx=18的根为________(结果精确到0.1). 分析大多数人往往拿起计算器就盲目代入数字计算,试图通过穷举来找到方程的根.事实上,使用计算器也得讲究方法.由题意知x>0.当x=1时,方程左边为1;当x=2时,方程左边为8.3;当x=3时,方程左边为27.477.因此,方程的根介于2与3之间,利用二分法的思想,代入x=2.5验算,左边为16.022 9,故方程的根介于2.5与3之间,再代入x=2.75验算,依次做下去最终得x≈2.6.故应填2.6. 注以上所举例题不仅可以用估算法解决,也可以用其他方法予以解决,但相比之下,用估算法解决这一系列客观题更显得事半功倍.因此,在平时学习中要注意多观察、多积累、多巩固,让估算成为常用的解题方法. [1] 黄益全.估算在高中数学解题中的应用[J].中学数学教学参考,2007(7):24-26. [2] 蔡勇全.漫话“五新”考题[J].中学生理科应试,2009(2):9-11. [3] 蔡勇全.确定恒成立不等式中参数范围的九种策略[J].中学数学研究,2010(11):33-35. [4] 蔡勇全.领悟一组“孪生”结论解决一类函数问题[J].中学数学研究,2011(2):40-41. [5] 蔡勇全.如何避免分类讨论[J].中学生理科应试,2011(7):7-8.
7 借助形数转换进行估算


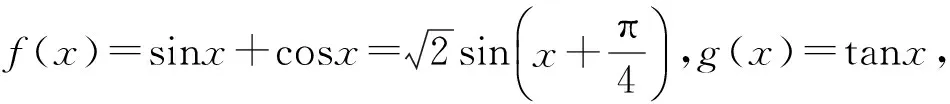



8 借助特例进行估算

9 借助二分法思想进行估算
