由一道中考压轴题引发的教学思考

●

宁海中学分校 江苏南京 210036)

由一道中考压轴题引发的教学思考

●卜以楼

宁海中学分校 江苏南京 210036)

1 问题提出

1．1 问题

2009年北京市数学中考试卷的最后一道压轴题为：

(1)求点D的坐标.

(2)作点C关于直线DE的对称点F,分别联结DF，EF.若过点B的直线y=kx+b将四边形CDFE分成周长相等的2个四边形，确定此直线的解析式.

(3)设G为y轴上一点，点P从直线y=kx+b与y轴的交点出发，先沿y轴到达点G，再沿GA到达点A，若点P在y轴上运动的速度是它在直线GA上运动速度的2倍，试确定点G的位置，使点P按照上述要求到达点A所用的时间最短(要求：简述确定点G位置的方法，但不要求证明).

图1 图2

1．2 参考答案

本题评分时，提供的参考答案如下(如图2所示)：

△DMC∽△AOC.

又

从而

得

故

FT=CS.

因为

FE=CD，

所以

TE=FE-FT=CD-CS=SD.

又因为

EC=DF，

所以TE+EC+CS+ST=SD+DF+FT+TS,

∠BAH=30°.

在Rt△OAG中，

笔者对第(1)和第(2)小题的参考答案没有疑异，对于第(3)小题的参考答案认为有“太平淡”之感.虽说题目要求是“简述确定点G位置的方法，不要求证明”,但是提供的确定点G位置的方法有“从天而降”、“丈二和尚摸不着头”、“意犹未尽”之感.学生作出点G的方法有相当大的偶然性和较大的投机成分,影响考题的信度和效度.

但是要确定点G的位置不是一件容易的事，在初中阶段是一道难题！笔者就如何确定点G的位置问题，对参考答案作如下补充，以求同行批评指正．

2 补充解答

由题意,可判定在y轴上的线段OM以外的点不符合条件，则点G必在线段OM上，因此确定点G的位置不外乎有以下2种方法.

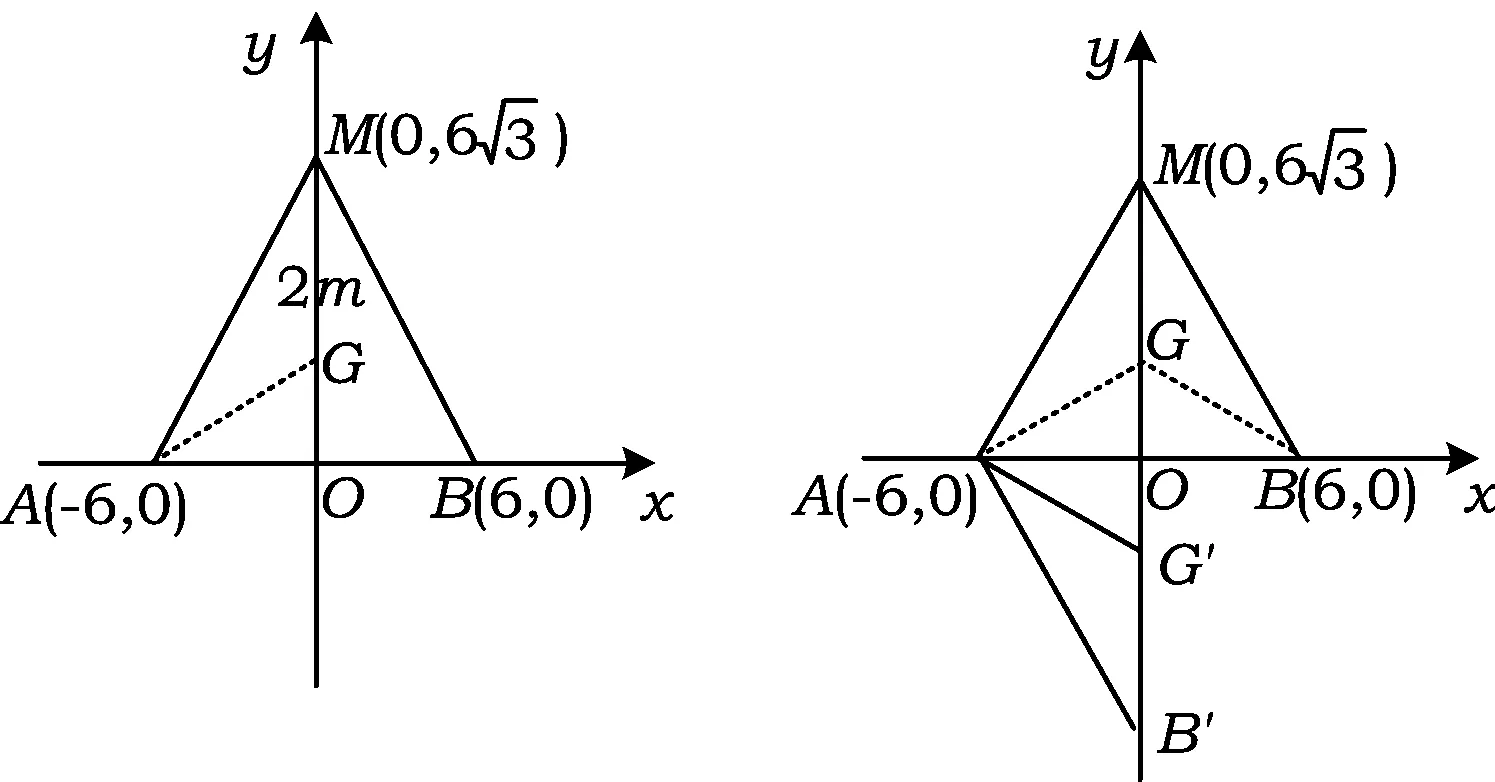
图3 图4

2．1 以数定点

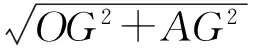
再设点G在MG上和GA上所用的时间分别为t1，t2，在GA上运动的速度为v，则点G在MG上运动的速度为2v，因此点G在MG和GA上运动的总时间为

因为

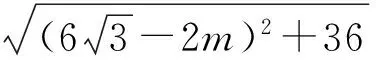
所以

整理，得

因为m为实数，所以

从而

解得

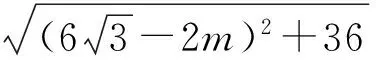
解得

则

∠GAO=30°．

2．2 以形定点

由2.1的解答过程可知点G在MG和GA上运动的总时间为

由于v是一个常量，原问题即求MG+2GA的最小值．联结GA，GB,由于△MAB为正三角形,GA=GB，因此问题就转化为求MG+GA+GB的最小值．将△AGB绕点A按顺时针旋转60°至△AG′B′位置时，显然有G′B′=GB，G′A=GA,∠GAG′=60°，则△AGG′为正三角形，GG′=GA，即

MG+GA+GB=MG+GG′+G′B′.

根据两点之间线段最短，当M，G，G′，B′这4个点共线时，MG+GG′+G′B′最短．此时在正△AGG′中，

又在正△MAB中,过点A作AH⊥BM于点H，则AH与y轴的交点即为所求的点G．

3 教学启示

探讨本题的解法，给我们的教学带来的启示主要有以下几点：

3．1 要适度坚持教“所以然”

新课程下的数学教学内容较多地采用“学生‘做’—在‘做’中感受和体验—主动获取数学知识”的呈现方式，在学生通过“做”获得感受的基础上，揭示具体“事例”的数学本质，然后再明晰有关知识，以此来加大用合情推理的方式探索图形性质的时空，为初中数学教学提供了崭新的视野和清新的气息，并在教学实践中获得了丰硕的成果．但是，在教学过程中要处理好合情推理与演绎推理的关系，要防止过度倡导合情推理、过分削弱演绎推理等极端局面的发生，矫枉不能过正，顾此不可失彼．

在引导学生通过“做”感受数学、探索知识和获得结论的同时，还要注意适度引导学生思考“为什么”——不仅让学生“知其然”，更要让学生“知其所以然”．因为“为什么”比“是什么”更重要，更具有思辨性，更具有教育价值．在教学过程中，要注意经常进行“小题大作”(多问几个“为什么”)，以此来打通各知识间的通道，放大各知识间的节点，凸显知识的来龙去脉．

3．2 让“双基”教学与“思想方法”教学同行

一方面，要继续保持“双基”的优势．“双基”教学是我国数学教学的特色之一，我们理应取其内核，继续发扬，对数学知识结构中的“基本模块”应该在“双基”中进一步贯彻与落实，编织功能齐备的“双基链”，以形成厚实的数学基础．

另一方面，要继续重视数学思想方法的教学．初中数学应用题教学的思想方法主要是数学建模，建模的基本方法是数学抽象，即“符号化”，也就是将实际问题中的“文字语言”转化为数学中的“符号语言”，即用数学中的“符号语言”去表示事物的状态和特征．

从上述2.1的解答过程看，主要利用了勾股定理，行程问题中的路程、速度、时间的三者关系，一元二次方程，一元二次方程根的判别式等“双基链”求出最少时间，使问题获得了解决．整个过程体现了较多的数学思想方法和技巧，对于解答中考压轴题来说是必要的，也是必不可少的．

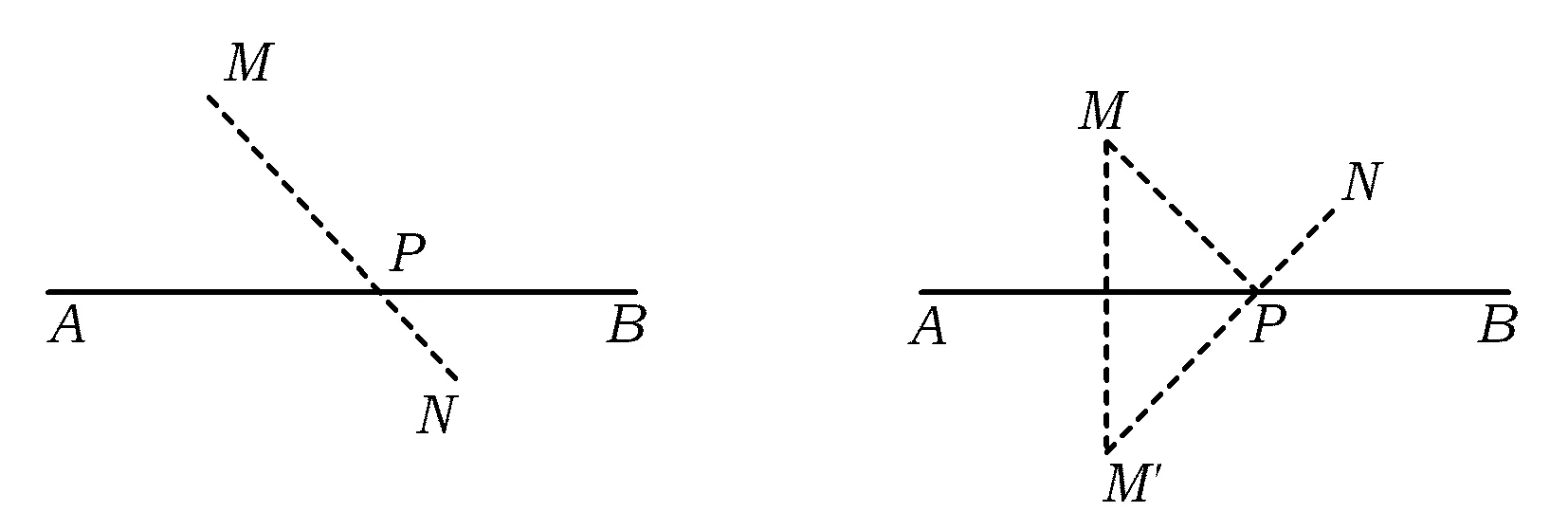
图4 图5

从2.2的解答过程看，其“双基链”主要有：

双基链1如图4所示，已知点M，N在直线AB的异侧，在AB上找一点P，使点P到M，N的距离和最小．

只要根据“两点之间线段最短”，将PM，PN这2条线段组合到一条直线上，即联结点M，N，交直线AB于点P，则点P就是要求的点．

双基链2如图5所示，已知点M，N在直线AB的同侧，在AB上找一点P，使点P到M，N的距离和最小．

只要将点M，N在AB的同侧转化成在AB的异侧即可．因此，可先找出M，N中的某一点关于直线AB的对称点，联结对称点与另一点交直线AB于点P，则点P就是要求的点．

从“双基链1”、“双基链2”，提升到本文要讨论的问题本质：

即把线段MG，GA，GB首尾联接在同一条直线上，根据“两点之间线段最短”来确定点G的位置．将△AGB绕点A按顺时针旋转60°至△AG′B′的位置，则MG+GA+GB=MG+GG′+G′B′，当点M，G，G′，B′共线时，MG+GG′+G′B′最短．

将本文要讨论的问题作一般化处理，便可得到下列一个有趣的问题(可称为“双基链3”)：

双基链3在三角形所在的平面里求一点，使该点到三角形3个顶点的距离之和最小，人们称这个点为“费马点”．

2.2的解答过程中反映的数学思想方法主要是“转化与化归”：将“双基链1”通过轴对称变换转化为“双基链2”；将“双基链1”通过中心对称变换转化为“本文要讨论的问题”．

综上所述，“双基”教学与“思想方法”教学同行的核心方法就是：一方面，把“大题”分解成“小题”，使“大题小作”；另一方面，让“小题”组合成“大题”，使“小题大作”．

3．3 适度避免“大题小作”

本题只要求确定点G位置的方法，但不要求说理证明，这样有于提高得分率．因为有相当一部分学生是凭借直觉思维与合情推理来完成解答的．在正△MAB中，只有一个点是特殊点，那就是△ABM的重心，有部分学生靠运气而得分．因此，本题考查的信度和效度还有待提高，有“大题小作”之嫌．

“大题小作”对于培养学生的直觉思维以及合情推理能力有较大的益处，但也应该承认直觉有时具有偶然性，这对培养学生思维的缜密性具有负面效应，特别是在解决中考压轴题时．对于本题，确定点G的位置，学生是靠运气、直觉判定来完成解答，还是靠合理的逻辑推理来完成，从解题要求和参考答案来看是无法界定的，很难达到选拔、区分的目的．事实上，要确定点G的位置，需要大量的思维过程和思维总量，对于初中阶段的学生来说，笔者认为不是一件容易的事！因此，我们要适度避免“大题小作”．

[1] 王润中．对一道中考压轴题“遗留”问题的探讨[J]．中小学数学，2010(Z1)：65-66．