基于模糊评价的体质健康评价隶属函数的建立——兼与2篇论文的商榷

王国军 ，王 辉 ，席 翼

国民体质评价中，通常采用百分位数法、离差法等确定等级上下限。该方法在大面积推广和使用时存在的问题是，临界点“指标值”接近但“等级”评定却相差甚远。如国民体质评价中台阶指数评分（20～24岁年龄段）：46.1为“1分”，而46.2为“2分”，评价结果显然不公平、不合理，减小了评价效能（如台阶指数58.1～67.6，虽进步存在困难，但仍属于同一等级，使进步效果不明显）。另外，当前体质健康综合评价，类似的事例看似极端却又不可避免，如血压评价时可能出现收缩压139 mmHg属于正常范畴，而140 mmHg属于高血压范畴的尴尬境地。随着模糊数学在综合评价中的成功应用，且人的体质好坏又无明确的衡量标准，“优”、“良”这类概念又具有明显的模糊性，因此，模糊数学的出现为科学地进行体质健康评价提供有效途径，使上述尴尬也随之得到解决。隶属程度的思想是模糊数学的基本思想，应用模糊数学方法的关键在于建立符合实际的隶属函数，确立隶属函数是模糊数学应用于体质健康评价的首要任务。

早在1965年，美国控制论专家扎德（L.A.ZADEH）教授就提出模糊数学的概念[1]。然而，自提出已过去多年，令人奇怪的是此方法在体质健康综合评价中的应用仅10余篇报道，且集中在八九十年代[2-8]，近期又零星出现相关报道[9-11]；巧合的是国外情况也类似，主要应用于疾病的判定和分级，如糖尿病性神经病、肥胖等[12-14]。分析已有资料发现：应用性研究中用于群体评价较常见，其模糊隶属度的确立往往采用“模糊统计方法”[10，15]；另一类则应用于个体体质健康的评价，这类往往采用“指派方法”，郭业才[5]和王晓东[6]的研究就属于此类，其建立的隶属函数在体质评价领域具有非常重要的引导意义，但也可能因处于探索初期，尚存在不完善之处。这类研究本就甚少，还存在质疑点，且也未交待更多关于如何建立隶属函数的理论基础及程序，知其然而不知其所以然现象普遍存在，可能正因如此，此评价方法并未如大众期望那样蓬勃发展。

鉴于此，本研究基于上述2文研究中的质疑点，理论简述如何通过指派方法建立隶属函数并最终确立体质健康评价中常用的“4等级”和“5等级”隶属函数模型，以期为今后模糊数学在体质健康综合评价中的应用提供一定的理论参考依据。

1 2文隶属函数中的质疑点

1.1 2文中的隶属函数

1.1.1 郭业才（“文1”）确立的隶属函数 该文评价对象是青少年个体体质，其评语集设定为：U={V1，V2，V3,V4,V5}，其中，V1=“良好”，V2=“较好”，V3=“一般”，V4=“较差”，V5=“落后”，与之对应的隶属度为 μ1、μ2、μ3、μ4、μ5，即属“5 等级”隶属函数，具体函数为：

式中，x表示该指标在抽样群体中的均值，s表示标准差，x为被测对象的实测值，以下同。

1.1.2 王晓东（“文2”）确立的隶属函数 该文的评价对象是学生个体体质，其评语集设定为：U={U1，U2，U3,U4}，其中，U1=“优”，U2=“良好”，U3=“一般”，U4=“差”，与之对应的隶属度为 μ1、μ2、μ3、μ4，即属“4 等级”隶属函数，具体函数为：

1.2 质疑点

1.2.1 分母中的“2” 不难发现，2文所建立的函数中，隶属度除直接表示为“1”和“0”之外，其他任一隶属函数的分母均为“2s”，应用中导致隶属度中未直接给出“1”时出现2个问题：（1）隶属函数最大值仅为0.5且存在无法逼近或等于“1”的情况，如“文1”中的μ（2x）函数，当时，隶属函数理应有最大隶属度值，而结果仅为0.5，其潜在意义是：任何一个实测值在该等级中都不可能出现完全隶属于此等级的情况；（2）该隶属函数的区间仅为[0，0.5]，而并不是模糊数学理应的区间[0，1]。若隶属函数的值域仅为{0，1}，则正是经典集合理论中的“非此即彼”，并未发挥模糊数学中“亦此亦彼”的不确定优势，模糊数学的隶属度取值应为[0，1]，而2文中的隶属度取值仅为[0，0.5]。因此，去掉分母中的“2”则可以消除上述疑点。

1.2.2 部分隶属函数的定义域不全 模糊数学用于体质综合评价时，由评价因素与评语集形成一个模糊矩阵R=（rtj）m×n，i=1，2…m；j=1，2…n，且都有 rtj∈[0，1]。评价时，必须运用隶属函数计算出每个指标所在每个等级中的隶属度。2文都存在部分隶属函数定义域不全的情况，比如针对各自μ2（x）隶属函数分别计算“较好”和“良好”等级隶属度时，当实测值大于x+2 s时，则找不到对应的定义域及其相应的隶属函数，而现实中，这一情况并不少见。如以“文2”中的铅球指标为例，原文给出的铅球均值为807.4 cm，标准差为41.1 cm，实测值为853 cm，对其隶属函数细化，结果为：

从隶属函数可知，853 cm不属于此函数任何定义域范围内。

1.2.3 模糊函数略显绝对化 以“文1”的μ2隶属函数为例，按其题意，求“较好”隶属度时，只要实测值小于均值，但如此一来，“较好”等级中的隶属度就为“0”，即完全不属于此等级。而根据模糊数学的思想，隶属度即表示隶属于某定义域内的隶属程度，越接近“1”表示越贴近“是”，而越接近“0”表示越贴近“否”。对于本例，当实测值小于均值时，仅仅是隶属于“较好”程度更小而已，不应该完全排除在“较好”等级之外，具体将通过下文的新建隶属函数与原函数计算结果对比进行论证。

2.2.4 文中数学运算有误 2文均是如此，此处仅以“文1”中的身高为例

计算μ1：将x=150.0 cm与s=153.3 cm代入μ1隶属函数：

其实测值为153.3，隶属于x＜155.75区间，因此，其在“良好”的隶属度为0，而原文结果为0.76。

同理，依次求出 μ2、μ3、μ4、μ5分别为 0.287、0.2137、0.287、0，按原文要求归一处理，结果分别为 0、0.365、0.270、0.365、0，而与原文中的 0.76、0.24、0、0、0 分歧较大。结合实际思考，较易发现，153．3 cm 的身高大于均值（150．0 cm），但小于 x+s=（x+s=150．0+5．75=155．75），即起码应隶属于“一般”及以上，但绝对不属于“良好”等级范畴，而原文给出“良好”的隶属度为0．76，“较好”的隶属度为0．24，显然，与实际并不相符，因此，其隶属函数方程及数学运算值得商榷。

2 隶属函数的确立及应用

2.1 理论简述[15]

隶属函数确定的常用方法主要有4种，体质综合评价中，往往采用模糊统计方法和指派方法，鉴于从建立隶属函数的角度出发，此处重点探讨指派方法。

所谓指派方法，就是根据问题的性质套用现成某些形式的模糊分布，然后根据测量数据确定分布中所含的参数，常用的模糊分布有矩形分布、梯形分布等。为了便于操作，在这里给出指派（或选择）的大致方向。

偏小型模糊分布适合描述像“小”、“冷”、“差”等偏向小的模糊现象，其隶属函数的一般形式为：，其中a为常数，而f（x）是非增函数。

偏大型模糊分布适合描述像“大”、“热”、“优”等偏向大的模糊现象，其隶属函数的一般形式为：，其中a为常数，而f（x）是非减函数。

中间型模糊分布适合描述像“中”、“暖和”、“中等”等处于中间状态的模糊现象，其隶属函数可以通过中间型模糊分布表示。需要特别指出的是，确定模糊集隶属函数的方法多种多样，但这些方法所给出的隶属函数只是近似的。因此，需要在实践中不断通过学习，加以修改，使之逐步完善。

2.2 “4等级”、“5等级”常用隶属函数的确立

个体体质健康评价中，隶属函数建立原理、步骤大同小异，故此处只以“5等级”隶属函数建立为例。

2.2.1 临界点的确定 体质评价中等级确定往往采用百分位数法、离差法等，2文所选方法均是离差法。在定义等级时，若取“5 等级”，即为人们所熟知的“优”、“良”、“中”、“下”、“差”，表示为：

特别指出：上述等级划分仅依据“文1”列出，目的在于更好地理解2文提出的隶属函数建立方法，因此，没有对等级进行更多地理论论证和实践调查。临界点的确定不具有普遍推广意义，但等级的不同划分不影响隶属函数建立的原理，只是临界值做相应的调整即可，等级划分的详细原理及方法可参考《体育测量与评价》[16]。另外，此处列举等级划分时仅以数值越大其分值越高的指标为例（如握力），指标数值越大其分值越小的指标，根据上述等级定义时正好相反，即“优”应当是x≤x－2s，而“差”应当是 x≥x－2s，这类指标常见时间类项目（如反应时）。

2.2.2 “5等级”隶属函数的确立 （1）“优”等隶属函数。根据等级临界点可知，此体质评价隶属函数呈梯形分布，“优”等隶属函数属于偏大型分布（见图1）。

图1 “优”等隶属函数分布示意图Figure 1 The schematic dagram of“excellent”fuzzy membership function

所以“优”等隶属函数为：

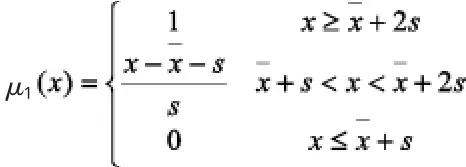
特别指出：上述函数仅适用于指标数值越大分值越高的项目（如握力），因此，等级内为递增函数。而对于时间类项目（如反应时），则应是递减函数，但其隶属函数建立原理与此类似，此处不再另外阐述，以下做相同处理。

（2）其他等级隶属函数。根据已界定好的等级临界点，绘出其它隶属函数（见图 2：a为“良”，b为“中”，c为“下”，d 为“差”）。其中，a、b、c为中间型模型分布，而d为偏小型模型分布。

按照求“优”等隶属函数的方法依次求出“良”、“中”、“下”、“差”4个等级的隶属函数，结果为：

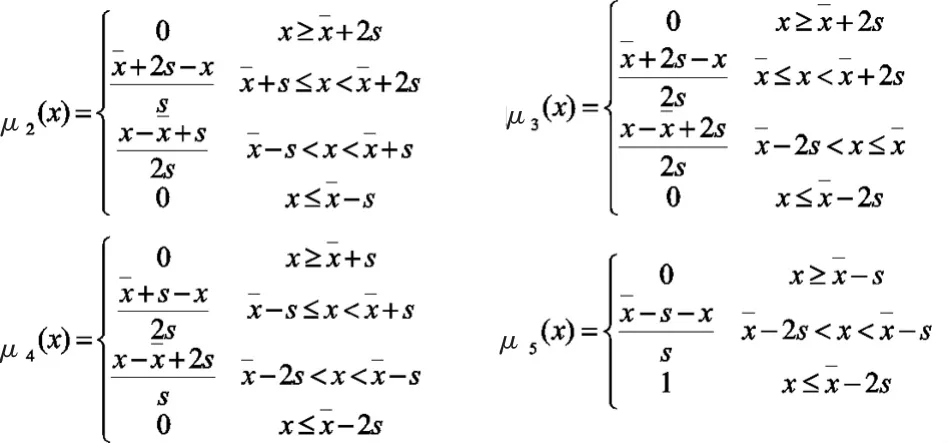
2.2.3 “4等级”隶属函数的确立 依据“五等级”隶属函数建立原理确立“4等级”隶属函数，结果如下：

2.3 新隶属函数的应用——基于2文的原始数据

2.3.1 “5等级”隶属函数的应用 以“文1”身高为例

x=153．3 cm 在“良好”等级的隶属度：x=153．3＜x+s=150．0+5．75=155．75，因此，在“优”的隶属度为 0，即 μ1=0。

图2 “良”（a）、“中”（b）、“下”（c）、“差”（d）隶属函数模型分布图Figue 2 The schematic diagram of"good"（a），"average"（b），"below average"（c），"poor"（d）fuzzy membership function model

同理，求出 μ3、μ4、μ5的结果分别为：0．713、0．213、0。归一化处理后 μ1、μ2、μ3、μ4、μ5的结果分别为：0、0．459、0．416、0．124、0，根据最大隶属原则可知，此人身高隶属“较好”。

2.3.2 “4等级”隶属函数的应用 以“文2”身高为例：x为170．99 cm，s=5．74 cm，x=172．2 cm。

求解过程同“2．3．1”，隶属度归一化处理后，μ1、μ2、μ3、μ4、μ5分别为：0、0．404、0．596、0，根据最大隶属原则可知，此人身高隶属“一般”。

3 讨 论

3.1 有效地解决体质评价中的尴尬事件

仍以身高为例，设有甲、乙2少年，其身高分别为151 cm和154 cm，借用“文1”中的等级分级标准、均值和标准差cm，s=5．75 cm）。根据分级可知：x－s=150－5．75=144．25；x+s=150+

若按原始等级标准判断，则甲的身高应属于“中”等。同理，乙虽极其靠近“较好”，但根据原始等级标准仍判定为“中等”。由此可知，甲、乙属同一等级，但乙明显靠近“较好”，且远离“中等”中心，显然评价不合理。若乙数据是甲在n年后的身高再测结果，虽然其已长高3 cm，但由于仍属同一等级，其长高这一结果难以体现。若此指标是某身体素质指标，那么其积极参与锻炼后的效果不明显，使得不合理评价可能挫伤其锻炼的积极性。

若按新建立的隶属函数计算，甲的隶属度结果为：μ1=0、μ2=0．587、μ3=0．913、μ4=0．413、μ5=0；乙为：μ1=0、μ2=0．848、μ3=0．652、μ4=0．152、μ5=0。根据最大隶属原则，甲身高属“中等”，而乙则属“较好”，与原始等级评价存在差异。

比较发现：运用新隶属函数不仅有效地区别甲与乙的实际差距，且根据隶属程度大小还很容易发现其身高真实属性，对乙而言，其身高隶属“较好”，隶属度贴近“1”，这与154 cm特别接近“较好”等级下限155．75 cm实际情况相符合。而甲的隶属度0．913几乎接近“1”，这与其身高151 cm无限接近“中等”中心150．0 cm 完全符合。

综上所述，若直接使用经典数学中的{0,1}取值，实践应用效果受限，而采用模糊数学思想，则有效地、合理地解决这类边界模糊的评价，隶属函数呈现出一定的缓冲段，“软着陆”的方式与实际情况更符合、更易接受。

3.2 新建隶属函数弥补区间仅为[0，0.5]的缺陷

新建任一非“0”和“1”的隶属函数中，都保证模糊函数的隶属度区间为[0，1]，弥补之前 2 文中区间仅为[0，0．5]且不连续的缺陷。如使用新建隶属函数计算2文身高等级情况时，身高隶属度结果就有大于0．5的情况存在，符合模糊函数求隶属度的目的及意义。

3.3 新建隶属函数解决原文中部分隶属函数定义域不全的情况

新建隶属函数中，每个等级隶属度求解过程实测值都能找到相应的定义域及其定义域所对应的隶属函数，即包含所有情况。

此处仍以铅球为例用新建隶属函数进行检验。按“文2”给出的铅球相关原始值进行隶属度计算，当实测值为853 cm时，其隶属度 μ1、μ2、μ3、μ4分别为：0．055、0．891、0．445、0，归一化处理后结果为 0．039、0．640、0．320、0。显然，实践检验过程中，没有出现找不到相应定义域的情况。

3.4 弱化原隶属函数模糊时略显绝对化趋势

2文中间型等级隶属函数，仅仅对相邻的2个区间进行模糊处理，出现如同“文1”中“较好”隶属等级时，只要实测值小于均值，则在“较好”等级中的隶属度就为“0”，即完全不属于此等级。为更好地解释其绝对化现象，此处以“文1”的“中”等为例进行说明（见图3）。

“文1”规定，当实测值小于x－s或者大于x+s时，隶属“中”等隶属程度为“0”，即完全排除在“中”等外。而实际情况并非如此，以某少年实测值为x+1．2s为例，分3种情况进行评价：

（1）在经典集合理论中，其隶属于“较好”等级，但不能否定的是，也特别接近“中等”等级（与中等下限 仅0．2 s的差距），显然，用经典集合理论评价出的结果说服力不足。

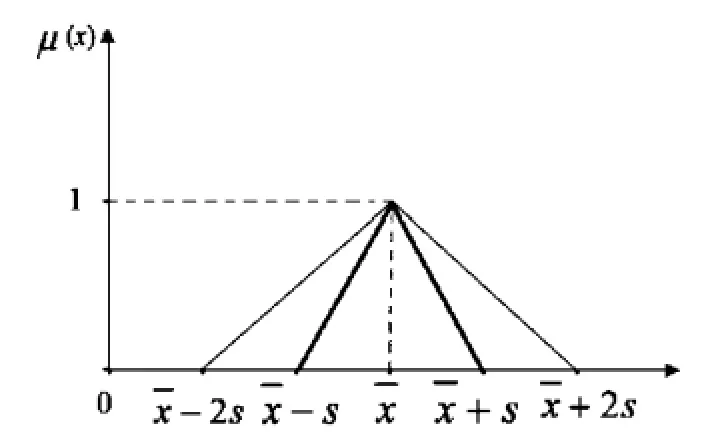
图3 新建隶属函数与“文1”原函数“中等”临界点选择对比Figue 3 The contrast of“average”critical point between new membership function and the primary function of“Literatures 1”

（2）按改进后的隶属函数计算结果为（改进时去掉分母“2”，且完善其定义域）：μ1=0.2，μ2=0.8，μ3=0，μ4=0，μ5=0。

（3）用新建的隶属函数分别求出其在各个等级的隶属度：μ1′=0.2，μ2′=0.8，μ3′=0.4，μ4′=0，μ5′=0，根据最大隶属度原则，其隶属于“较好”等级。

不难看出，第（1）种评价方式明显不合理，而第（2）和第（3）种评价的差别在于“中等”的取值：新函数中（μ′）为 0.4，而“文1”的（μ3）仅为 0。结合实际可知，x+1.2s隶属于“较好”但也贴近“中”，只是贴近程度不如“较好”而已。显然，隶属度值更加直观、详细地描述与各个等级之间的贴近关系，不仅更加符合实际，也更迎合模糊数学“亦此亦彼”的思想。

4 结论与建议

4.1 结论

（1）指出当前体质评价中使用指派方法建立模糊隶属函数时的一些质疑点，并以商榷的形式引起后续相关研究的关注。

（2）基于对疑点的总结，依据模糊隶属函数建立理论，建立体质评价中常用“4等”和“5等”隶属函数。

4.2 建议

（1）血压、脉搏这类指标不宜简单使用“离差法”进行等级划分，其在正常范围并非是越高或者越低越好，建议参照刘励[10]提供的方法进行评价。

（2）模糊数学评价的优势不仅仅解决单一指标的评价，其关键作用在于能合理解决边界模糊、量纲不统一的多类指标的综合评价。隶属函数的建立只是模糊数学使用中关键的一环或者其中一种方式，真正应用于实践时还需结合实际情况综合考虑。

[1]ZADEHL.Fuzzy sets[J].Information and Control，1965（8）：338-353.

[2]魏铁华.对模糊综合评判的加权方法及用统计法求模糊事件概率的探讨[J].华北电力学院学报，1986（2）：78-82.

[3]马生全，青峰.应用模糊数学方法对学生体质的综合评价[J].西北民族学院学报，1987（1）：60-66.

[4]马德胜.用于儿童青少年体质评价的Fuzzy二阶综合评判数学模型[J].体育科学，1987（4）：42-45.

[5]郭业才.青少年个体体质评价的模糊数学模型及其应用[J].中国医学物理学杂志，1994，11（4）：47-51.

[6]王晓东.关于学生体质评价的模糊数学模型 [J].辽宁工学院学报，1995，15（1）：89-92.

[7]何争流.模糊统计在体质综合评价中的应用研究 [J].浙江体育科学，1997，19（1）：60-62.

[8]王兆月，曹雅君，阎金禄.学生体质状况模糊综合评价及其软件编制[J].天津医科大学学报，1999，5（1）：80-82.

[9]刘励.儿童青少年体质健康的综合评价及影响因素研究[D].武汉：华中科技大学，2009.

[10]刘励，吴汉荣.模糊数学综合评价评判在初中生健康群体综合评价的应用[J].中国社会医学，2009，25（2）：160-161.

[11]赵书祥.体质综合评价中层次分析法的应用研究 [J].北京体育大学学报，2007，30（7）：938-940.

[12]MIYAHIRA SA，DE AZEVEDOJL，ARAUJOE.Fuzzy obesity index（MAFOI）for obesity evaluation and bariatric surgery indication[J].J Transl Med，2011（9）：134.

[13]SIGMUNDE，ZACPAL J，SIGMUNDOV A D.The application of formal concept analysis and the importance of scaleselection in the evaluation of physical activity data in relation to the body mass index[J].Acta Universitatis Palackianae Olomucensis.Gymnica，2010，39（4）：41-51.

[14]PICON A P，ORTEGA N R S，WATARI R，etal.Classification of the severity of diabetic neuropathy：a new approach taking uncer taintiesinto account using fuzzy logic[J].Clinics，2012，67（2）：151-156.

[15]谢季坚，刘承平.模糊数学方法及其应用[M].武汉：华中科技大学出版社，2006.

[16]孙庆祝.体育测量与评价[M].北京：高等教育出版社，2006.