金属疲劳裂纹扩展速率的贝叶斯正则化BP神经网络预测

罗广恩 ，崔维成

（1江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2中国船舶科学研究中心，江苏 无锡 214082）

1 引 言

船舶与海洋结构物绝大多数是由金属材料加工制造而成。由于其所处的工作环境载荷复杂、恶劣，结构物的疲劳问题受到广泛的关注。准确预报疲劳裂纹扩展寿命的关键因素之一就是确定疲劳裂纹扩展速率它直接影响到疲劳寿命预报结果的准确性。为描述疲劳裂纹扩展速率，通常将疲劳试验数据回归成公式，比较常用的有Paris-Erdogan公式、Forman公式等，这些公式各有特点。到目前为止，还没有一个可以适合所有金属材料的统一的疲劳裂纹扩展速率公式。

人工神经网络是20世纪40年代以来迅速发展起来的模拟人脑神经活动的一种新技术。适合处理复杂的线性和非线性关系，具有自主学习能力，能够建立难以用显示表达式表达的映射关系，并有较好的泛化能力。目前神经网络在智能控制、智能监测监控和智能故障诊断等方面应用较广，在疲劳领域也有很好的应用前景。Genel[1]通过建立BP网络用材料的拉伸性能数据预测了低周疲劳特性参数。Fotovati[2]用不同温度下的疲劳裂纹扩展速率实验数据训练BP网络，训练好的网络可以预测不同温度下的裂纹扩展速率。Haque[3]用BP网络预测了腐蚀环境下的疲劳裂纹扩展速率。国内，王珉[4]利用材料的常规力学性能训练BP网络来预测疲劳裂纹扩展公式（Paris公式）中的参数。顾玉钢[5]采用改进BP网络预测了疲劳裂纹扩展速率。纪冬梅[6]用BP网络预测了腐蚀环境下疲劳裂纹扩展率Forman公式中的系数C。

本文针对不同金属的疲劳裂纹扩展速率分别建立贝叶斯正则化BP神经网络，以一部分不同应力比R下的疲劳裂纹扩展速率为基础，预测其他应力比R下的疲劳裂纹扩展速率，从而达到减少试验次数，充分利用已有数据的目的。将从文献中获取的4种不同金属材料（铝合金6013、300M钢、铝合金2324和铝合金7055）的疲劳试验数据作为算例，来检验建立的贝叶斯正则化BP神经网络的性能。

2 神经网络的建立

BP神经网络是误差反向传播的前向型神经网络，其具有结构简单、性能可靠的特点，是目前应用广泛的一种网络。它由输入层、隐层和输出层组成。每层有若干个节点组成，每个节点代表一个神经元，层与层之间的节点通过权值和阀值连接，同一层节点之间没有联系。网络通过对训练样本的学习，是将网络的输出结果与目标结果之间的误差反向传播，修改各层的权值和阀值，如此迭代。最终使神经网络的输出结果与目标结果的误差最小。

2.1 三层BP网络

建立三层BP网络，即：输入层、隐层和输出层。输入层包含两个输入变量ΔK、r；隐层有N个神经元（N的具体数值见2.4）；输出层有一个变量，对应于三层BP网络结构图如图1所示。

2.2 输入数据的归一化

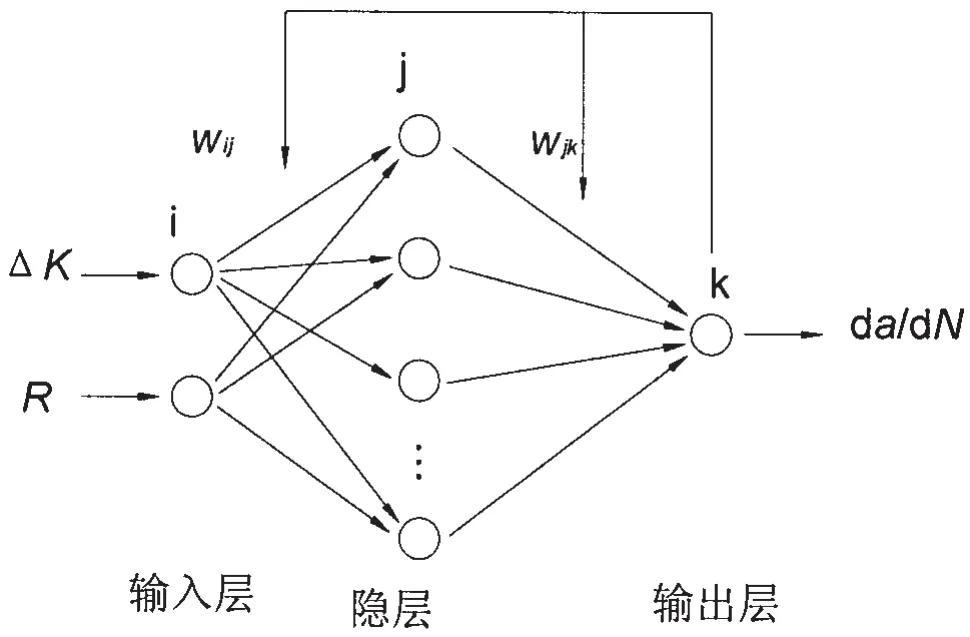
图1 三层BP网络结构图Fig.1 Structure of three layered BP network

2.3 传递函数

神经网络中传递函数决定了神经元不同的输出特性。

（1）Purelin函数（线性函数）

Purelin函数如图2所示，用数学表达如下：

（2） tansig函数（S型函数）

tansig函数如图3所示，用数学表达如下：

图2 Purelin函数图Fig.2 Graph of linear transfer function

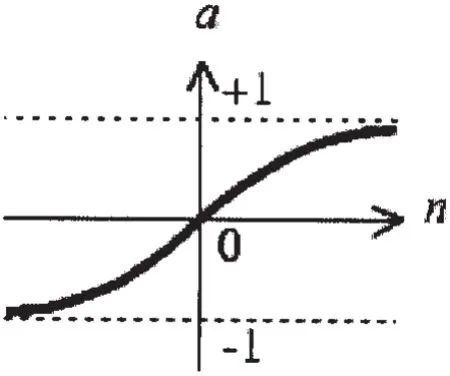
图3 Tansig函数图Fig.3 Graph of Tan-Sigmoid transfer function

2.4 隐层神经元个数的确定

在神经网络的建立过程中，隐层神经元个数的确定是一个非常重要的部分。个数设置太多，运行速度变慢，容易过度学习而出现过拟合，最终导致网络的泛化能力下降。目前，这方面还没有完善的理论，主要依据经验试算。本文引用文献[3]中的经验公式来确定隐层神经元的个数。

式中：Inputs为输入层单元的个数；Outputs为输出层单元的个数；number of training patterns为训练的样本个数。

2.5 贝叶斯正则化[7]

传统BP网络的性能函数F：

式中：ED为训练误差的平方和。

贝叶斯正则化网络性能函数F：

式中：EW为网络中权值的平方和；α和β为系数。

采用公式（6）作为性能函数，可以在保证网络误差最小的情况下，使网络具有较小的权值。亦即网络中的有效权值尽可能地小，这实际上相当于自动缩小了网络的规模。此外，性能函数中的系数α、β在常规的正则化方法中难以确定，但采用贝叶斯正则化方法可以在网络的训练过程中自适应地调整α、β的大小，并使其达到最优。因此，采用贝叶斯正则化BP网络具有更好的泛化能力。

本文采用Matlab语言和神经网络工具箱建立了贝叶斯正则化BP网络。

3 算例与分析

3.1 铝合金6013疲劳裂纹扩展速率预测

以不同应力比R下铝合金6013的疲劳试验数据为样本，建立贝叶斯正则化BP网络。铝合金6013试验数据[8]如图4所示。

将图4中的数据分为两部分，R=-1、0.1和0.5对应的疲劳裂纹扩展速率数据用于训练网络，R=0.3、0.7对应的数据用于测试网络，检验其泛化能力。

采用3层BP网络，包括输入层、隐层和输出层。隐层传递函数采用Tansig函数，输出层函数采用线性函数。中间层神经元个数按照公式（4）确定，N=0.5× （2+ 1）+取9个神经元。因此贝叶斯正则化BP网络结构为2-9-1。

用训练样本对已建立的网络进行训练，训练结果如图5所示。

图5中，首先从疲劳裂纹扩展速率曲线的角度来看，神经网络输出结果与试验结果的吻合度很好；其次，从具体的数据点角度来看，绝大部分数据点神经网络均能准确拟合。这表明网络的训练效果较好。

相比于对训练样本的拟合能力而言，我们更加关注神经网络对未经训练过的样本的预测能力。下面来检验贝叶斯正则化BP网络对疲劳裂纹扩展速率的预测能力，即对R=0.3时疲劳裂纹扩展速率进行预测，检验其内插能力；随后对R=0.7时疲劳裂纹扩展速率进行预测，检验其外推能力。预测结果如图6和图7所示。

（1）检验网络的内插能力

用训练好的网络对R=0.3时疲劳裂纹扩展速率进行预测，预测结果如图6所示。

图4 铝合金6013疲劳裂纹扩展速率试验数据Fig.4 Experiment results of fatigue crack growth rate of aluminum alloy 6013

图5 铝合金6013神经网络训练结果图Fig.5 Training result of neural network of aluminum alloy 6013

图6 铝合金6013疲劳裂纹扩展速率（R=0.3）神经网络预测结果Fig.6 Prediction results of fatigue crack growth rate(R=0.3)for aluminum alloy 6013 by neural network

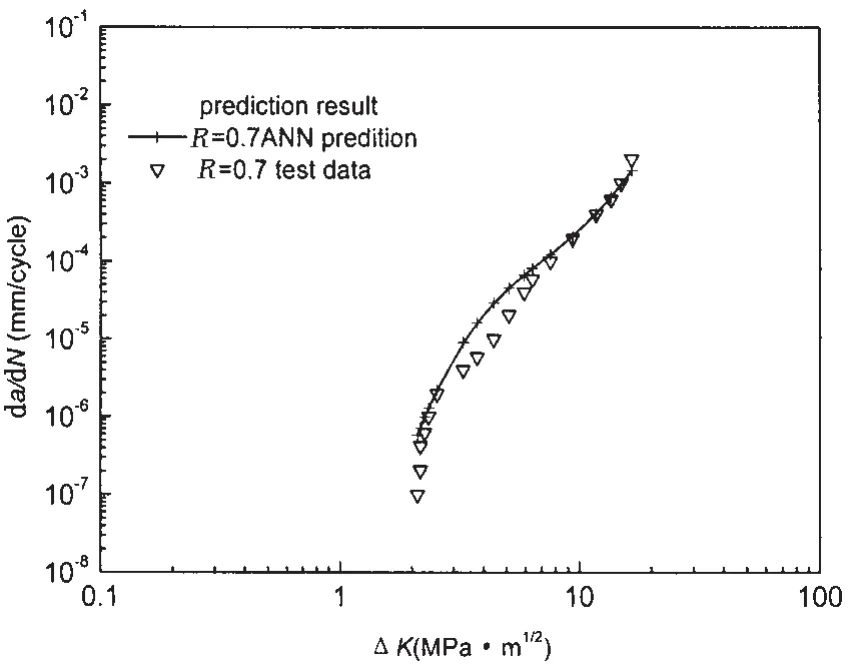
图7 铝合金6013疲劳裂纹扩展速率（R=0.7）神经网络预测结果Fig.7 Prediction results of fatigue crack growth rate(R=0.7)for aluminum alloy 6013 by neural network

从图6可以看出，贝叶斯正则化BP网络对疲劳裂纹扩展速率的内插预测效果相当理想，表明该网络有很强的内插能力。

（2）检验网络的外推能力

用训练好的网络对R=0.7时疲劳裂纹扩展速率进行预测，预测结果如图7所示。

对比图6和图7两者的预测效果，可以发现该网络的外推能力比其内插能力要稍弱一些，这也是神经网络的一个弱点。从图7可以看出，神经网络外推预测结果与试验结果在部分数据点上存在一定误差，但从数据点构成的曲线来比较，两者还是基本吻合的。总体来说，预测效果令人满意。

3.2 300M钢疲劳裂纹扩展速率预测

以不同应力比R下300M钢的疲劳试验数据为样本，建立贝叶斯正则化BP网络。

300M钢试验数据[9]如图8所示。

将图8中的数据分为两部分，R=0.05、0.5对应的疲劳裂纹扩展速率数据用于训练网络，R=0.3、0.7时的数据用于测试网络，检验其泛化能力。

同样，采用3层BP网络。隐层传递函数采用Tansig函数，输出层函数采用线性函数。中间层神经元个数按照公式（4）确定，N=0.5×（2+）1，取9个神经元。因此贝叶斯正则化BP网络结构为2-9-1。

用训练样本对已建立的网络进行训练，训练结果如图9所示。

图9表明，网络的训练效果较好。

图8 300M钢疲劳裂纹扩展速率试验数据Fig.8 Experiment results of fatigue crack growth rate of 300M steel

图9 300M钢神经网络训练结果图Fig.9 Training result of neural network of 300M steel

图11 300M钢贝叶斯正则化BP网络预测R=0.7时的疲劳裂纹扩展速率Fig.11 Prediction results of fatigue crack growth rate(R=0.7)for 300M steel by neural network

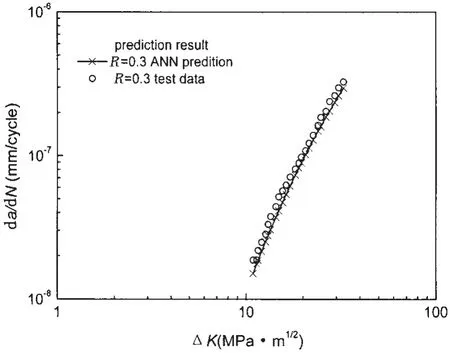
图10 300M钢疲劳裂纹扩展速率（R=0.3）神经网络预测结果Fig.10 Prediction results of fatigue crack growth rate(R=0.3)for 300M steel by neural network

下面我们来检验贝叶斯正则化BP网络对疲劳裂纹扩展速率的预测能力，即对R=0.3时疲劳裂纹扩展速率进行预测，检验其内插能力；随后对R=0.7时疲劳裂纹扩展速率进行预测，检验其外推能力。预测结果如图10和图11所示。

（1）检验网络的内插能力

用训练好的网络对R=0.3时疲劳裂纹扩展速率进行预测，预测结果如图10所示。

从图10可以看出，贝叶斯正则化BP网络对疲劳裂纹扩展速率的内插预测效果相当理想，表明该网络有很强的内插能力。

（2）检验网络的外推能力

用训练好的网络对R=0.7时疲劳裂纹扩展速率进行预测，预测结果如图11所示。

图11表明，外推预测结果与试验结果吻合。综合图10和图11可以得出，300M钢贝叶斯正则化BP网络有很强的内插和外推能力。

对比铝合金6013与300M钢网络的预测效果，可以看出后者的预测能力明显要强于前者。分析这两者试验数据的差异，初步推断门槛值附近样本点的减少是导致网络预测能力提高的原因。

3.3 铝合金2324疲劳裂纹扩展速率预测

接下来，以不同应力比R下铝合金2324的疲劳试验数据为样本，建立贝叶斯正则化BP网络。

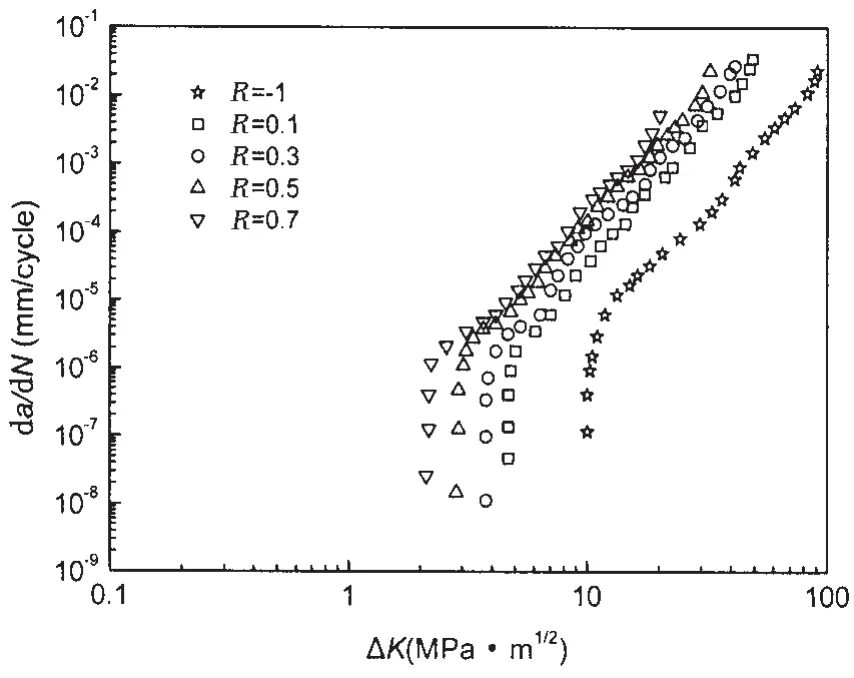
图12 铝合金2324疲劳裂纹扩展速率试验数据Fig.12 Experiment results of fatigue crack growth rate of aluminum alloy 2324

图13 铝合金2324疲劳裂纹扩展速率试验数据（采用的）Fig.13 Experiment results of fatigue crack growth rate of aluminum alloy 2324(adoptive)

铝合金2324试验数据[8]如图12所示。考虑到各应力比下疲劳裂纹扩展速率在门槛值附近的数据点较多，接近于垂直线。为了提高网络的训练和预测性能，舍去一些门槛值处的数据点。最终用于训练网络和测试网络的数据样本如图13所示。

将图13中的数据分为两部分，R=-1、0.1、0.5对应的疲劳裂纹扩展速率数据用于训练网络，R=0.3、0.7时的数据用于测试网络，检验其泛化能力。

BP网络采用3层结构，隐层传递函数采用Tansig函数，输出层函数采用线性函数。中间层神经元个数按照公式（4）确定，N=0.5×（2+ 1）+=9.81，取10个神经元。贝叶斯正则化BP网络结构为2-10-1。

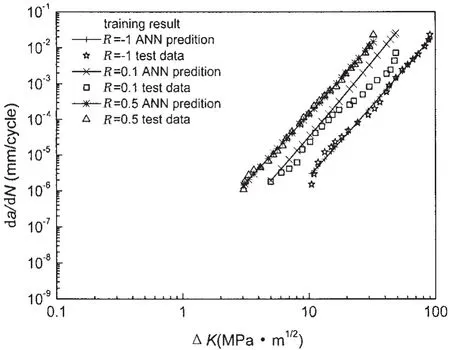
图14 铝合金2324神经网络训练结果图Fig.14 Training result of neural network of aluminum alloy 2324

用训练样本对已建立的网络进行训练，训练结果如图14所示。

下面我们来检验贝叶斯正则化BP网络对疲劳裂纹扩展速率的预测能力，即对R=0.3时疲劳裂纹扩展速率进行预测，检验其内插能力；随后对R=0.7时疲劳裂纹扩展速率进行预测，检验其外推能力。预测结果如图15和图16所示。

图15 铝合金2324疲劳裂纹扩展速率（R=0.3）神经网络预测结果Fig.15 Prediction results of fatigue crack growth rate(R=0.3)for aluminum alloy 2324 by neural network

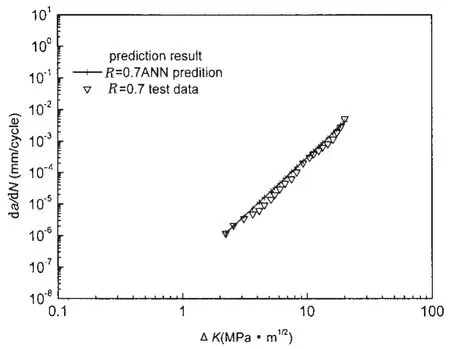
图16 铝合金2324贝叶斯正则化BP网络预测R=0.7时的疲劳裂纹扩展速率Fig.16 Prediction results of fatigue crack growth rate(R=0.7)for aluminum alloy 2324 by neural network

（1）检验网络的内插能力

用训练好的网络对R=0.3时疲劳裂纹扩展速率进行预测，预测结果如图15所示。

（2）检验网络的外推能力

用训练好的网络对R=0.7时疲劳裂纹扩展速率进行预测，预测结果如图16所示。

从图15和图16可以看出，网络具有较强的预测能力，包括内插与外推功能。

3.4 铝合金7055疲劳裂纹扩展速率

以不同应力比R下铝合金7055的疲劳试验数据为样本，建立贝叶斯正则化BP网络。

铝合金7055试验数据[8]如图17所示。基于2.3中同样的考虑，舍去一些门槛值处的试验数据点，最终用于训练网络和测试网络的数据样本如图18所示。

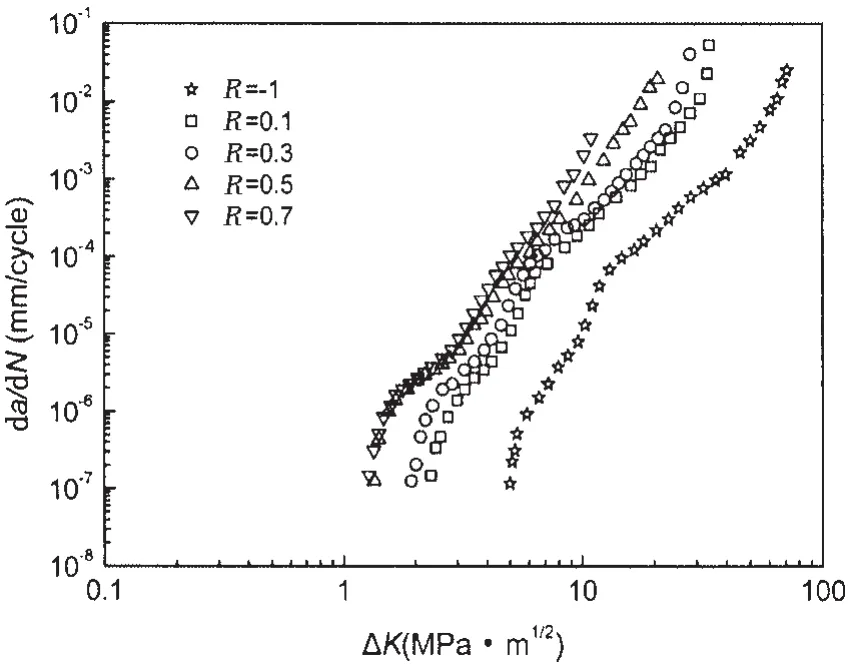
图17 铝合金7055疲劳裂纹扩展速率试验数据 Fig.17 Experiment results of fatigue crack growth rate of aluminum alloy 7055

图18 铝合金7055疲劳裂纹扩展速率试验 数据样本（采用的）Fig.18 Experiment results of fatigue crack growth rate of aluminum alloy 7055(adoptive)

将图18中的数据分为两部分，R=-1、0.1、0.5对应的疲劳裂纹扩展速率数据用于训练网络，R=0.3、0.7时的数据用于测试网络，检验其泛化能力。

BP网络采用3层结构，隐层传递函数采用Tansig函数，输出层函数采用线性函数。中间层神经元个数按照公式（4）确定，N=0.5×（2+ 1）+=10.56，取11个神经元。 因此贝叶斯正则化BP网络结构为2-11-1。

用训练样本对已建立的网络进行训练，训练结果如图19所示。

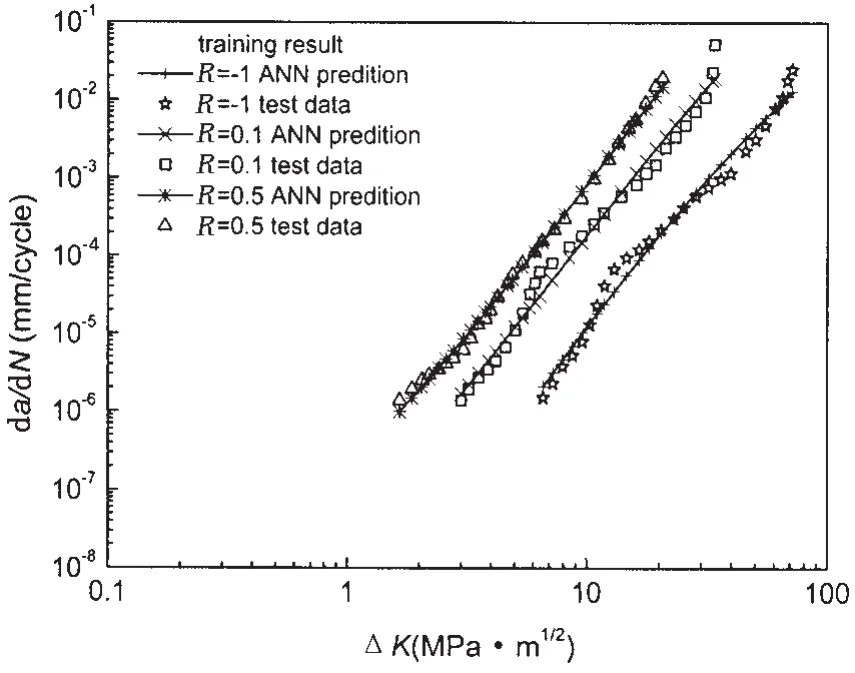
图19 铝合金7055神经网络训练结果图 Fig.19 Training result of neural network of aluminum alloy 7055

图20 铝合金7055疲劳裂纹扩展速率（R=0.3）神经网络预测结果Fig.20 Prediction results of fatigue crack growth rate(R=0.3)for aluminum alloy 7055 by neural network

下面我们来检验贝叶斯正则化BP网络对疲劳裂纹扩展速率的预测能力。

（1）检验网络的内插能力

用训练好的网络对R=0.3时疲劳裂纹扩展速率进行预测，预测结果如图20所示。

（2）检验网络的外推能力

用训练好的网络对R=0.7时疲劳裂纹扩展速率进行预测，预测结果如图21所示。

图20和图21表明，贝叶斯正则化BP网络有较强的预测能力。同时也进一步证明了我们的推断，即舍去门槛值附近的一些数据点可以提高网络的预测能力。

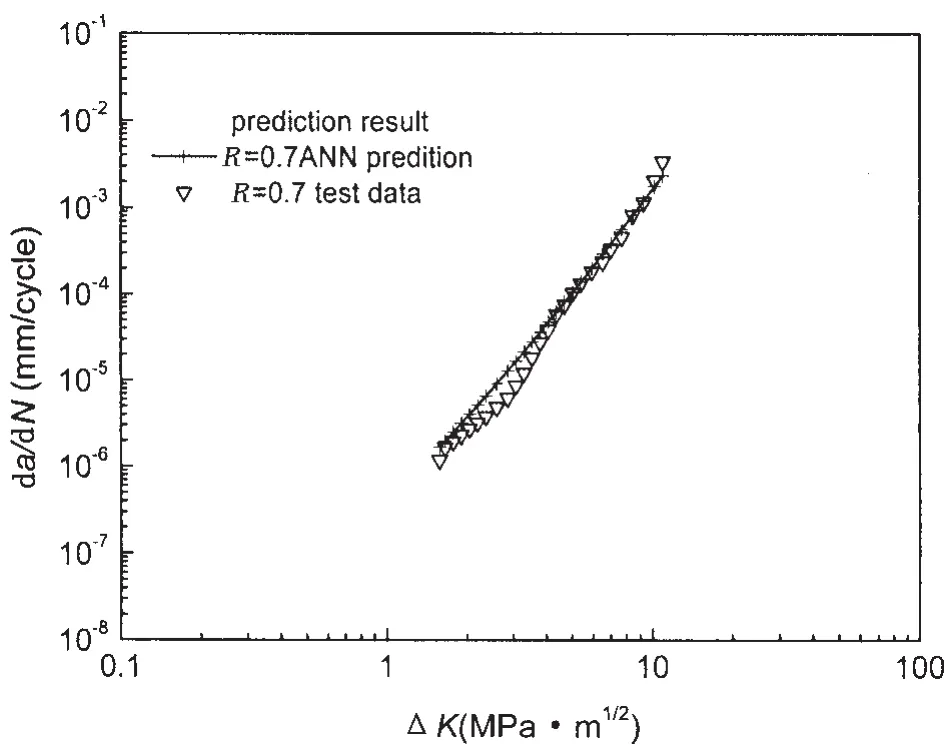
图21 铝合金7055贝叶斯正则化BP网络预测R=0.7时的疲劳裂纹扩展速率Fig.21 Prediction results of fatigue crack growth rate(R=0.7)for aluminum alloy 7055 by neural network

4 结 论

本文针对金属疲劳裂纹扩展速率建立了贝叶斯正则化BP神经网络。并通过对4种不同金属材料的疲劳裂纹扩展速率试验数据分别进行神经网络训练和网络预测。结果表明：

（1）贝叶斯正则化BP神经网络能够较好地拟合不同应力比下的疲劳裂纹扩展速率；

（2）贝叶斯正则化BP神经网络对于测试样本有较好的预测能力，包括内插和外推能力，即具有较强的泛化能力；

（3）在贝叶斯正则化BP神经网络使用过程中，舍去一部分门槛值附近的样本点可以提高网络的预测能力。

因此，该方法可以方便地获得不同应力比R下的疲劳裂纹扩展速率，从而达到减少试验次数，充分利用已有数据的目的。并且可以进一步应用于其他金属的疲劳裂纹扩展速率的预报。

[1]Genel K.Application of artificial neural network for predicting strain-life fatigue properties of steels on the basis of tensile tests[J].International Journal of Fatigue,2004,26(10):1027-1035.

[2]Fotovati A,Goswami T.Prediction of elevated temperature fatigue crack growth rates in TI-6AL-4V alloy-neural network approach[J].Materials&Design,2004,25(7):547-554.

[3]Haque M E,Sudhakar K V.Prediction of corrosion-fatigue behavior of DP steel through artificial neural network[J].International Journal of Fatigue,2001,23(1):1-4.

[4]王 珉,郎福元,龚 俊,等.基于神经网络的疲劳裂纹扩展率的初步估算[J].甘肃工业大学学报,2001,27(4):29-32.

[5]顾玉钢,夏智海,庄力健.基于改进神经网络的疲劳裂纹扩展速率预测[J].合肥工业大学学报,2008,31(6):937-941.

[6]Ji D M,Zhou C Y,Hu Y R.Crack growth rate of 07MnNiCrMoVDR steel in H2S solution[J].Journal of Ship Mechanics,2005,9(6):103-112.

[7]MacKay D J C.Bayesian interpolation[J].Neural Computation,1992,4:415-447.

[8]Paris P C,Tada H,Donald J K.Service load fatigue damage-a historical perspective[J].International Journal of Fatigue,1999,21:35-46.

[9]Dinda S,Kujawski D,Correlation and prediction of fatigue crack growth for different R-ratios using Kmaxand ΔK+parameters[J].Engineering Fracture Mechanics,2004,71(12):1779-1790.