基于工艺可行性的离散变量结构动力特性设计优化

黄海燕，林志祥，王德禹

（1江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2云南农业大学 水利水电与建筑学院，昆明 650201；3上海交通大学 海洋工程国家重点实验室，上海 200030）

1 引 言

近年来，超大型船舶和高速船舶的出现，使得船体结构振动问题越来越突出。船舶结构在动载荷作用下的结构响应在很大程度上依赖于结构前几阶固有频率。为了避免共振现象的发生，必须使结构的固有频率值与激励力频率值之间存在一定的差异。前者大于或小于后者一定的百分比，即设置一个频率禁区，使之满足频率储备要求。但频率储备值过大，将使结构过于笨重；储备值过小，则可能导致振动剧烈。对结构进行动力特性优化设计[1-3]是一种抑制或减少有害振动的、行之有效的振动控制方法。单一工况下所获得的结果往往是该给定载荷工况下的最优解。这个最优解对于其他工况则不一定是最优解。在船舶运营过程中，不同的海况和不同的装载，会形成不同的计算工况。因此，要想使结构优化真正进入工程实用阶段，进行多工况结构优化设计研究势在必行。借鉴协同优化算法的思想，论文首先建立多工况下船体结构动力特性设计优化模型，并提出基于工艺可行性分析和使用自适应模拟退火算法的设计流程，然后以船艉结构的动力特性优化设计为算例，对模型进行验证分析。

2 结构动力特性优化模型

多工况意味着在结构的正常使用期限内，不同的时间可能独立作用有不同的载荷或载荷集。不同工况将会导致结构产生不同的结构响应。在某种程度上，多工况下的最优设计追求的是一种最优的折衷设计。

2.1 数学模型

多工况下船体结构动力特性优化模型的数学表达式为

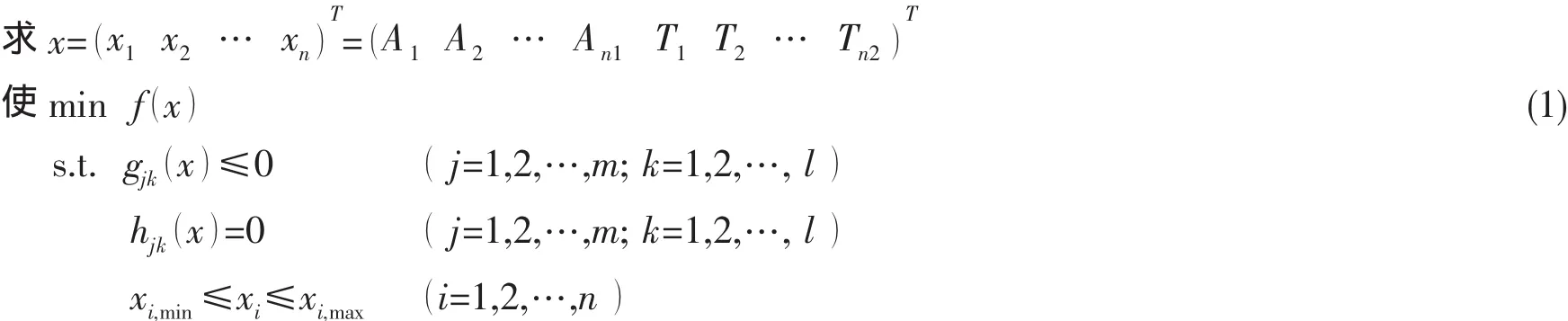
式中xi为设计变量；n为设计变量总数；Ai为板材厚度，共n1个；Ti为骨材型号，共n2个；l为载荷工况数目；m为约束总数；gjk（x）、hjk（x）分别为第k个工况下的第j个不等式约束和等式约束；xi,min和xi,max分别为第i个设计变量的下、上限。

（1） 目标函数

为了尽可能地获得更理想的工程造价，选择结构总质量最小化为目标函数，即在满足各种载荷工况作用下的约束条件，使结构重量尽可能的小。

（2） 设计变量

在船舶结构优化设计中，由于船舶的主尺度参数是确定的，所以只能选择构件尺寸作为设计变量。通常是选择板材厚度和骨材尺寸为设计变量。按设计变量类型的分类，它们属于离散变量。在优化过程中，当选取骨材尺寸作为独立的设计变量时，型材的尺寸参数 H、W、t1、t2（如图 1所示）之间的协调变化很难得到保证。因为所有的型钢尺寸必须符合既定规格的要求，否则将会导致船厂买不到相应型号的型钢，或必须向工厂专门定制。因此，本文选取板材厚度和骨材型号为设计变量，并建立相应的离散集。该集合可用一个矩阵来描述[4]。

图1 骨材设计变量Fig.1 Design variables of beam

由板材厚度构成的离散集的矩阵描述为

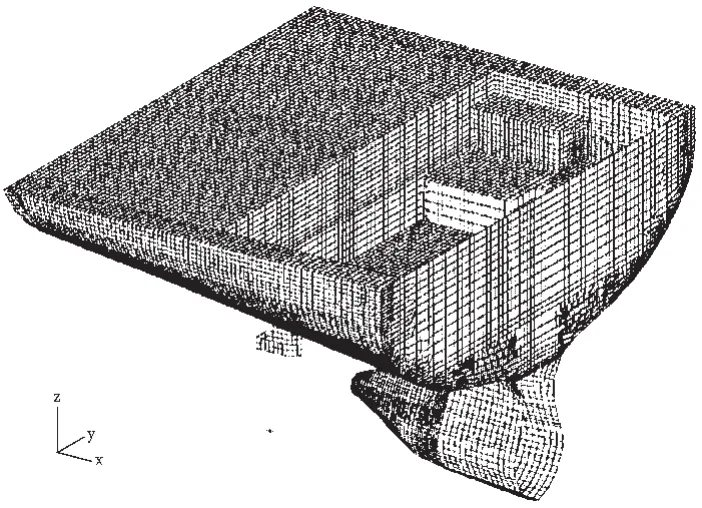
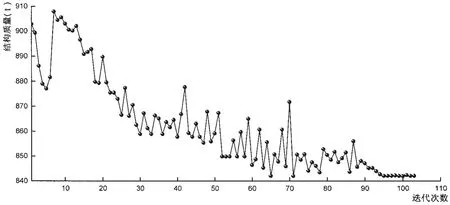
式中Ai为第i个设计变量；Aij为第i个设计变量的第j个取值；k1为离散变量可取值的个数；为了程序编写的方便，规定离散值的取值顺序为Aij-1

船舶结构中使用的型材截面通常有L型、T型和矩形截面等。它们均可使用四个尺寸参数描述其截面尺寸：H、W、t1、t2，如图1所示。对矩形截面骨材，t1=t2=0。由型材型号构成的离散集的矩阵描述为

式中 Ti为第 i个设计变量； （H 、W、t1、t2）ij为第i个设计变量的第j个取值，这4个参数在程序中由一个4维数组构成；k2为离散变量可取值的个数；为了程序编写的方便，规定离散值的取值顺序由H的取值决定，即 Hij-1

根据约束条件和各船级社规范，确定每一个设计变量的取值集合，构成一个数据库，在每次优化时，供优化程序调用。

（3） 约束条件

约束条件主要有几何约束和频率禁区约束。几何约束条件的一般表达为

式中xi,min为约束下限，一般为静力条件下限或结构合理性下限；xi,max为约束上限，一般为工艺要求上限；ns为约束条件个数。

频率禁区约束条件的一般表达为

式中fi为第i阶频率；fi,min、fi,max分别为频率禁区的下限和上限；nf为频率约束条件个数。

此外，还有按振动衡准要求设定的最大位移约束；考虑腐蚀和稳定性等要求设定的最小板厚约束；考虑结构合理性要求设定的最大板厚约束。

2.2 工艺可行性分析

计算机软件完成的结构优化设计只是参数意义上的优化，计算机软件不会考虑优化参数在工艺上的可实现性。软件分析的结果可能将结构某些部位构件厚度取很小或很大的数量级；或者构件厚度在结构的局部部位减少或增加。这种优化结果在生产工艺上无法实现，只能是一种概念化设计[5]。因此，在优化过程中，必须考虑节省工时和工艺上的可操作性。在重量变化不大的前提下，尽量减少不同板厚、板宽的材料规格，以及型材和组合型材的规格，尽量少使用船厂难以订到的板厚规格、型材，以减少定货时间和费用。

2.3 优化算法

自适应模拟退火算法ASA（Adaptive Simulated Annealing）是一种高效快速的全局优化算法，用以解决具有多峰和非光滑性的高难度非线性优化问题[6]。ASA算法的优点是能够获得全局最优解而不是局部最优解、对初始条件的要求低、肯定收敛且收敛速度较快。因此，选用ASA算法为优化算法。

2.4 结构优化设计流程

在优化设计过程中，需要选择结构中对工艺影响较小、同时结构响应对该部件的灵敏度值较大的部件进行优化。针对船舶结构设计的特点，基于工艺可行性分析和使用ASA算法的结构动力特性优化设计流程如图2所示。

图2 结构优化设计流程Fig.2 Design flow of structure optimization

图3 船艉结构有限元模型Fig.3 Finite element model of ship stern

3 算例分析

以某集装箱船的艉部结构FR-10～FR+28（如图3所示）的动力特性设计优化为算例，对论文提出的动力特性优化模型进行验证分析。

3.1 有限元模型

采用4节点板壳单元模拟板。在连接两个网格密度不同的区域时选用3节点板壳单元，同时确保疏密网格的过渡平滑。采用2节点梁单元模拟型材单元，并考虑偏心的影响[7]。采用2节点杆元模拟支柱。采用偏心质量单元模拟集装箱质量、压载水舱水质量、舵叶质量和螺旋桨质量，同时考虑质量惯性矩。空船结构质量和舾装等非结构质量按肋位以密度定义的分布质量方式计入。节点总数为62933个；单元总数为93280个。在肋位FR+28处，采用固定端约束。

3.2 优化分析

在船舶结构设计时，在模型中同时将所有工况考虑是不可能的，也是不必要的。满载和压载工况是船舶运营过程中的两种典型工况，因此，本文针对这两种工况的组合进行多工况优化设计分析。

在船艉结构有限元模型中，板材厚度和骨材型号共计50个参数。根据设计响应对设计变量的灵敏度计算结果[8]，从中选择了 15 个参数作为优化设计变量：A0109、A0210、A0310、A0410、A0812、A1412、A1512、A1713、A1814、A1915、A2115、A2315、A2416、T05、L09，如表 1 所示。 本文借鉴协同优化算法的思想[9]，将全体设计变量设置为共享设计变量，使用同一个目标函数，使其分别满足各自工况下的约束条件。

当生产工艺发生较大变化时，可能导致工程造价产生较大的提高。当厚度差超过4 mm的不同厚度钢板对接时，厚板应在一定范围内削斜。例如优化前结构的第14号参数A1412和第18号参数A1814的厚度差为2 mm。在优化过程中，将这两个参数的厚度差小于或等于4 mm作为工艺可行性评定标准之一。此外，对于个别构件，如果采用火工成形时，其板材厚度在理论最优解的基础上至少增加1 mm作为加工余量。

表1 设计变量初始值和最优解对比（单位:mm）Tab.1 Comparison between the initial and final design variables

使用Lanczos方法和模态参与因子提取技术，提取结构前三阶固有频率。系统经过103次迭代达到收敛。目标函数（结构质量）的迭代历史如图4所示。优化前的结构质量为902.813 t，优化后的结构质量为842.057 t；质量减少60.756 t，即质量减少6.73%。设计变量的初始值和最优解对比如表1所示。结构固有频率的初始值和最优解对比如表2所示。

图4 目标函数迭代历史Fig.4 Convergence history of structural mass

从上述分析结果可以看出：

（1）本文建立的动力特性优化模型能应用于多工况下工程结构的实际优化设计中。将设计变量处理为共享设计变量的方法是可行的、正确的。

（2）优化前、后结构的第1、3阶固有频率均满足规范要求。

（3）满载时，第2阶固有频率由优化前的1.4541 Hz变化为优化后的1.4166 Hz，即频率储备由优化前的11.74%增加到优化后的14.51%。压载时，第2阶固有频率由优化前的7.4272 Hz变化为优化后的7.3584 Hz，即频率储备由优化前的11.74%增加到优化后的12.56%。这大大降低了结构发生共振的概率。

4 结 语

针对船体结构设计的特点，论文建立了基于工艺可行性的船体结构动力特性优化模型；使用矩阵描述由板材厚度和骨材型号构成的离散设计变量集；为适应多工况的计算需求，将设计变量设置为共享设计变量；并提出了基于ASA算法的优化设计流程。以组合工况作用下的船艉结构动力特性优化设计为例，对模型进行了验证分析。优化后的船艉结构增加了频率储备，降低了结构自重，达到了预期目标。

[1]魏发远,李世其,钟毅芳.带频率约束的浸水圆柱壳结构优化设计[J].应用力学学报,2002,19(1):6-9.

[2]夏利娟,余 音,金咸定.卫星构架结构固有频率特性的试验研究和优化设计[J].上海交通大学学报,2004,38(11):1889-1891.

[3]张 丽,王德禹.考虑弯扭强度和频率约束的集装箱船中剖面优化设计[J].船舶工程,2008,30(2):1-4.

[4]郭鹏飞,韩英仕,魏英姿.离散变量结构优化的拟满应力设计方法[J].工程力学,2000,17(2):94-98.

[5]蔡东升,李建康.基于工艺可行性的带频率禁区结构动态优化设计[J].机械设计与制造,2006,9:1-3.

[6]Ingber L.Adaptive Simulated Annealing(ASA):Lessons learned[J].Control and Cybernetics,1996,25(1):33-54.

[7]黄海燕,王德禹.加筋板结构的自由振动分析[J].船舶工程,2008,30(6):1-4.

[8]黄海燕,王德禹.基于灵敏度的多学科优化设计变量的模糊分析[J].上海交通大学学报,2009,43(8):14-18.

[9]Huang haiyan,Wang Deyu.Static and dynamic collaborative optimization of ship hull structure[J].Journal of Marine Science and Application,2009,8(1):77-82.