一种与JPEG图像压缩编码结合的细胞自动机域盲水印算法

吴慧琳 周激流 龚小刚 李炳法 文 扬 尹 皓

①(四川大学电子信息学院 成都 610064)

②(四川大学计算机学院 成都 610064)

1 引言

数字水印是将一个信号(水印)以不可见方式嵌入另一个信号(宿主信号，原始信号)的处理过程，其中宿主信号可以是图像、音频或视频；被嵌入的水印信号最后可以被提取或检测出来。自1954年水印技术问世以来，已经涌现出大量适用于不同应用的静态图像的水印算法。现有的数字图像水印算法多适用于静态图像；而近年来国际上趋向于采用简单可行的软硬件实现水印算法[1]。因此结合了数字图像水印技术与图像压缩标准的、计算复杂度低、易于硬件实现且健壮性较好的压缩图像水印算法吸引了许多研究人员进行研究。

细胞自动机变换提供了一种把细胞自动机理论和数学、物理、工程等理论联系起来的工具[2]；被用于图像增强、边缘检测、降噪处理、图像加密等；但将其及其变换应用到数字图像水印中，是近几年才开始出现的。文献[3]提出一个基于细胞自动机变换的数字图像水印算法的框架结构。文献[4]利用细胞自动机的混沌特性，对图像进行扩频调制将水印嵌入在图像的频域。文献[5]利用细胞自动机的分形特性来对图像进行处理，并将水印嵌入处理后的图像中。文献[6]提出一个基于细胞自动机变换的水印算法，该算法适用于普通未压缩的图像，且水印的提取需要依赖原始图像。

JPEG是当前广泛使用的图像压缩标准之一，与其相关的水印算法，按照算法输入输出的不同大体可以分为两类。第1类的输入输出均为JPEG压缩文件，如文献[7,8]；第 2类的输入为原始文件，输出为 JPEG 文件，如文献[9-11]。其中大部分算法是在进行JPEG压缩的量化步骤时嵌入水印。本文的算法，属于第2类。

本文结合JPEG图像压缩编码和细胞自动机，提出一种用于JPEG压缩图像的数字盲水印算法。该算法先用Moore型细胞自动机对水印图像进行置乱；随后用细胞自动机变换对原图进行分解，并在分解后得到的低频系数子带中嵌入置乱后的水印信息。最后将嵌入了水印的图像按JPEG图像压缩标准进行编码。水印的提取是在解码过程中进行的。实验证明该算法在保证水印不可见性的同时，对常见的攻击如JPEG压缩攻击，滤波攻击，高斯噪声攻击，旋转攻击等有较好的鲁棒性。

本文余下部分的内容安排如下。第2章提供了关于细胞自动机的理论基础。第3章先介绍了基于细胞自动机的图像置乱；同时详细给出了基于JPEG 图像压缩编码的细胞自动机域数字盲水印算法的嵌入与提取算法。第4章展示了仿真实验与实验结果。第5章是结论。

2 背景知识

2.1 Moore邻域细胞自动机

Moore邻域是由细胞aij自身及其上、下、左、右的4个细胞，与对角线上4个细胞共同构成，如图1(a)中所示，表达式如式(1)。

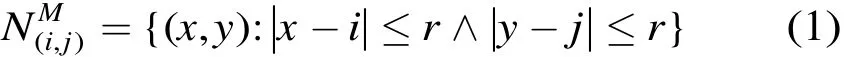
若状态集S={ 0,1}，邻域半径r=1,Moore邻域细胞自动机的局部规则为“外全加”如式(2)所示。规则编号由式(3)确定。

其中s表示状态集的个数；n表示细胞邻域内元素个数。根据组合排列，可以得知共有 22×9=262144种映射，即规则。

2.2 二维细胞自动机变换

细胞自动机变换(Cellular Automata Transform,CAT)的主要优势是可以得到大量不同性质的正交、半正交、双正交，非正交等的基函数。

(1)变换与逆变换 由N×N个细胞构成的二维细胞空间，二维细胞自动机变换与逆变换如式(4)所示。

其中fij表示原始图像系数；ckl表示变换系数；是细胞自动机基函数。如式(5)所示，本文采用由一维细胞自动机基函数衍生二维细胞自动机基函数的方式，即Type8类型基函数。

其中Lw≥ 2 表示的是细胞可能有的所有状态的数量。在二值状态的细胞自动机空间，二维细胞自动机基函数可表示为式(6)。

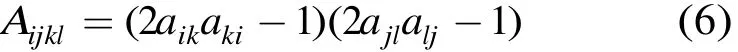
(2)图像的细胞自动机变换 细胞自动机变换是一种分层编码方案[12]。设给定原始图像为w×h，其中w=2m,h=2n(要求m和n都是正整数，若2的整数次幂则通过补0的方式满足要求)。将原始图像分成 2 (m+n)/(8 × 8)个字块，每个子块有 64个像素。对每个子块进行二维正交细胞自动机变换，则变换系数Ckl落在4个不同的子带中。即当k和l都为偶数时，Ckl为低频系数。将所有表示低频的系数分离出来，可以组成一幅新的低分辨率图像，称为 LL子带。k为偶数和l为奇数时，得到 HL子带；k为奇数和l为偶数时，得到LH子带；k和l都为偶数时，得到HH子带。后3个子带，均表示图像的高频部分，如图1(b)所示。图1(c)展示的是一个Type8类型二维正交基函数。图1(d)是对图像 Baboon进行二维细胞自动机变换分解后，得到的4个子带图。

3 与JPEG图像编码结合的细胞自动机域盲水印算法

本文所提的与 JPEG图像编码结合的水印算法，其整体流程如图2所示。

3.1 水印嵌入算法

如图3所示，为水印嵌入算法图示。

(1)用二维 Moore型细胞自动机对二值水印图像进行置乱。设需要置乱的图像I，大小为m×n，I(i,j)表示图像I在(i,j)的像素值。演化次数(迭代次数)为k。P是m×n的零矩阵，设置计数器t=0 。水印图像置乱算法步骤如下：

(a)由种子δ生成与图像I等大同维的随机矩阵E0，其中只含有0和1元素。

(b)将随机初始矩阵E0与图像I按坐标位置一一对应起来。按光栅扫描线顺序，从上到下、从左到右扫描E0。每当扫描到E0(i,j)=1,1 ≤i≤m,1≤j≤n，就按顺序将图像I中(i,j)位置的像素值取出来，以扫描线策略存放在P中。

(c)选取具有混沌性质的总和规则，将E0作为Moore邻域细胞自动机初始构形，若t＜k，则执行①到③步操作。

①依照总和规则进行一次迭代演化，将得到的构形记录到一个新矩阵Et+1中。Et+1与图像I等大同维。

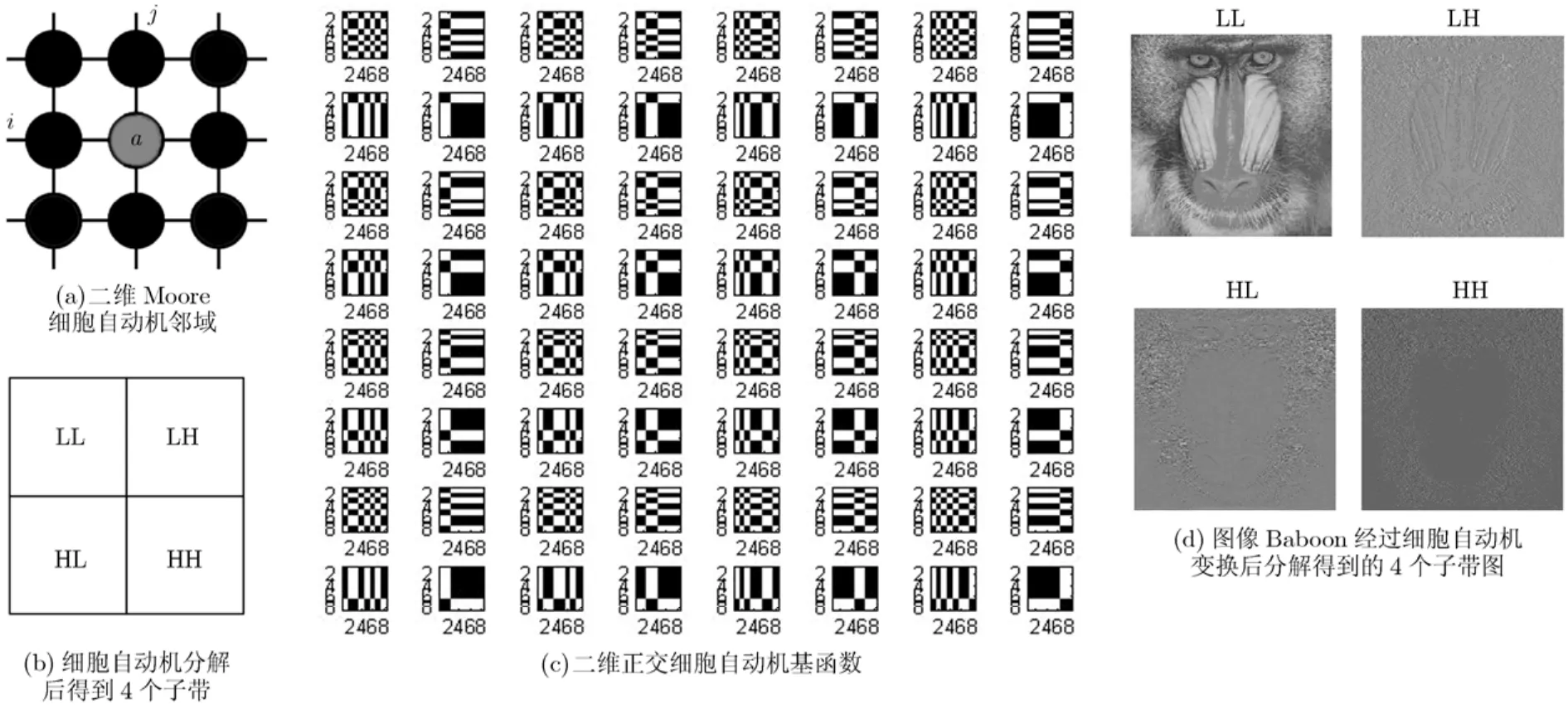
图1 Moore邻域细胞自动机

图2 本文算法中的与JPEG图像编码结合的水印算法

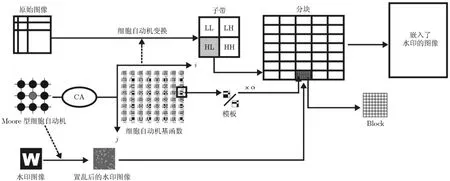
图3 水印嵌入算法图示

②按扫描线顺序：从左到右、从上到下依次将同时满足式(7)条件的(i,j)对应的图像I(i,j)像素值取出，存放在矩阵P中。

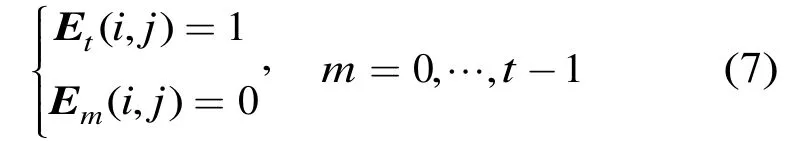
③令t=t+ 1 。

(d)将I中剩余未被提走的像素按扫描线顺序取出，依次加到P中。最后P就是置乱后的水印图像矩阵。

k次迭代演化，得到一组构形序列：{E1,E2,…,Ek}。只要细胞自动机的总和变换规则号固定，种子δ不变，则会得到同样的构形序列。将构形序列序列也即是置乱算法的迁移路线，将E1和Ek相接形成环路，则以置乱后的图像矩阵P作为初始构形，沿着迁移路线一步一步回退，最终可以得到原图I。综上，反置乱步骤与置乱步骤顺序相反，需要将规则号和种子δ作为密钥。

(2)用包括Wolfram规则号、细胞邻域、细胞初始构形、边界等在内的几个关键值，生成一个二维正交细胞自动机基函数Bij(i,j=1,2,…,8)。

(3)对原始图像进行一级正交细胞自动机变换。变换后得到4个子带。其中一个是低频子带LL，其余均是高频子带。由于LL是存有图像的大量信息，选择高频子带HL嵌入水印。

(4)将高频子带HL分成不重复的块，每个块包含8×8=64个像素。每一块将被嵌入一位水印。

(5)生成两个小于 8的随机整数x和y，目的是为了组合起来得到一个坐标(x,y)。然后从64个基函数中选择坐标为(x,y)的基函数子块作为一个模板P1=Bij(i=x,j=y)。由于细胞自动机的基函数取值范围S={ 0,1}，对选择的模板P1取反，则得到模板P0。

(6)用两个模板P1,P0以及一个强度因子α，根据式(8)，将置乱后的水印按位(watermark bit)嵌入到HL子带中。

(7)执行细胞自动机逆变换，将所有分块重组，得到嵌了水印的图像。

(8)对图像进行标准JPEG压缩处理。即将嵌了水印的图像分成8×8的块，对每个块进行DCT变换。随后使用64元素量化表，对每个64的系数进行量化。量化后的系数，采用Zigzag扫描方式进行扫描，最后使用Huffman编码方式进行编码。这些操作完成后，就可以得到嵌入了水印的压缩图像数据。

3.2 水印提取算法

如图2中所示，本算法的解码，是在标准JPEG解码器的离散余弦反变换(IDCT)步骤后多了一个水印提取处理模块。该模块主要是从重建的图像中提取水印，其操作步骤如下：

(1)对嵌入了水印的JPEG压缩图像数据，进行反熵编码，反Zigzag扫描，反量化，离散余弦反变换(IDCT)等操作。得到一个重建的图像信号。

(2)使用与水印嵌入算法中相同的细胞自动机关键值，生成相同的二维正交细胞自动机基函数Bij(i,j=1,2,…,8)。

由于不同的关键值，可以生成不同的细胞自动机基函数；所以当关键值不同时，细胞自动机基函数就无法被反算出来。这就增加了水印算法的安全性。

(3)对重建的图像信号进行细胞自动机变换。得到4个细胞自动机变换系数子带。

(4)选取HL低频系数子带，将其分成多个互不重叠的分块，每一块大小为8×8。

(5)用与嵌入算法中相同的两个随机整数x和y，组合为坐标(x,y)。从64个基函数中选择一个基函数，即模板P1；求补集得到模板P0。

(6)用模板P1(或模板P0)，与HL低频系数子带的每一个8×8的分块进行相关性判断，从而将嵌入在每一分块中的每一位水印(watermark bit)提取出来，提取如式(9)所示。

(7)将提取出来的水印图像，进行Moore型细胞自动机反置乱。反置乱步骤与 3.1节中置乱步骤顺序相反。

4 实验与结果

为了检验本文水印算法的性能，选取了3个大小均为512×512的灰度图Lena,Crowd和Goldhill进行多组试验。其中图 Lena含有较小的细节；图Crowd相比之下含有大量的细节。以二值图像‘W’(32×32)作为水印图像。用于生成Type8正交细胞自动机基函数的关键值如表1所示。

表1 产生Type8型的细胞自动机关键值

选取具有混沌性质的，规则号为224的；转换规则为外全加规则；对应的映射函数f(1,2)=1,f(0,3)=1,f(1,3)=1且其他状态值均为0的Moore型细胞自动机对二值水印图像进行置乱。设定置乱次数k为100。

4.1 隐蔽性分析

在不改变图像压缩率的前提下，水印的隐蔽性与式(8)中的强度因子α相关。α取值较小时算法具有很好的水印隐蔽性，鲁棒性较差。α取值较大时算法鲁棒性较好，水印隐蔽性较差。在理想状况下，经过多次实验发现，当强度因子取值为4时，本文算法的水印隐蔽性较好。故本实验强度因子取值为α=4 。

为了对水印算法进行客观的评价，本文用峰值信噪比(Peak Signal Noise Ratio,PSNR)作为一个衡量标准，以便清晰地判断出原始图像和受到攻击后的嵌有水印的JPEG压缩图像之间的差别，如式(11)所示。

用归一化相关系数(Normalized Correlation,NC)作为提取出的水印与原始水印相似度的评价指标。NC值越大，表明两者相似度越大，即水印提取效果越好。NC定义如式(12)所示。

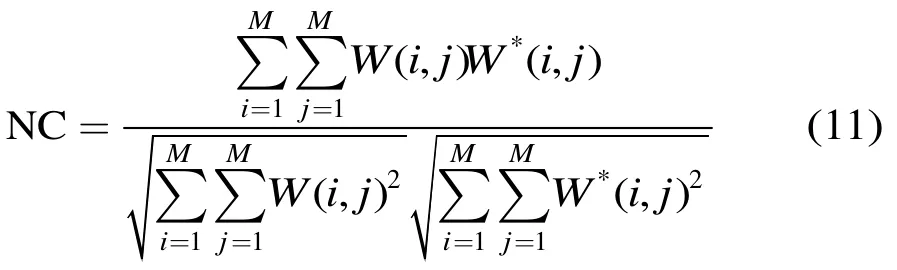
对图像Lena,Crowd和Goldhill分别进行水印嵌入和水印提取实验。图4显示的是Lena图实验结果。其中4(a)是Lena原始图像；4(b)表示未嵌入水印的JPEG压缩格式的Lena。此时图像的压缩比为4.0815,PSNR为33.07。4(c)是嵌入了水印的JPEG压缩格式Lena。原始图像与嵌入了水印的JPEG格式Lena的图像压缩比为3.8370,PSNR为32.63。此时原始水印与提取出来的水印的NC值为0.98。此外，图像Crowd与图像Goldhill的实验结果为：(1)Crowd：原始图与未嵌入水印的JPEG格式图像的压缩比为2.6336,PSNR为26.14。原始图与嵌入了水印的JPEG格式图像的压缩比为2.5428,PSNR为26.05。此时原始水印与提取出来的水印的NC值为 0.9698。(2)Goldhill：原始图与未嵌入水印的JPEG格式图像的压缩比为2.5550,PSNR为26.84。原始图与嵌入了水印的JPEG格式图像的压缩比为2.4521,PSNR为26.72。此时原始水印与提取出来的水印的NC值为0.9844。

图4 Lena的实验结果

从视觉上看，嵌入了水印的压缩图像与原图基本一致。由实验结果可以得出，嵌入了水印以后的图像的压缩率有所降低，PSNR有所减小，但是提取出来的水印与原始水印的相似度很高。说明本文水印算法的隐蔽性较好。

4.2 鲁棒性检测实验

为了检测水印的鲁棒性，我们对 Lena,Crowd和Goldhill分别进行了几组攻击实验。包括加性噪声攻击，高斯低通滤波攻击，剪切攻击，旋转攻击，JPEG 压缩攻击，直方图均衡化攻击以及线性锐化攻击等。实验结果表明该算法具有较好的鲁棒性，且可以将NC值(约0.8)，作为对水印图像存在的阈值。实验结果如表2所示。

表2 从各种攻击实验提取出来的水印图像及相关性能数据

5 结论

本文提出了一种与JPEG图像压缩编码相结合的细胞自动机域数字盲水印算法。该算法不同于常规压缩图像水印算法，首先利用Moore型细胞自动机对水印图像进行置乱。随后对图像进行细胞自动机变换，变换后的系数被分为4个子带；选取其中表示低频系数的子带，将置乱后的水印图像嵌入；利用反变换生成嵌入水印后的图像。最后，对嵌入了水印的图像进行JPEG压缩编码，得到压缩后的嵌入了水印的图像。即本文所提水印算法可以用于JPEG压缩图像。水印的提取是在JPEG解码过程中进行的；实验证明，该算法在保证水印不可见性的同时，对常见的攻击如JPEG压缩，滤波，加性噪声攻击等有较好的鲁棒性。

[1]Ni Zhi-cheng,Shi Yun-qing,et al..Reversible data hiding[J].IEEE Transactions on Circuits and Systems for Video Technology,2006,16(3): 354-362.

[2]Lafe O E.Method and apparatus for data encryption/decrption using cellular automata transform[P].Patent,USA,5677956,1997.

[3]Reiko Shiba,Seok Kang,and Yoshinao Aoki.An image watermarking technique using cellular automata transform[C].TENCON 2004,2004 IEEE Region 10 Conference,Japan,2004,1: 303-306.

[4]Vijay Harishchandra Mankar,Tirtha Sankar Das,et al..Cellular automata based robust watermarking architecture towards the VLSI realization[J].World Academy of Science,Engineering and Technology,2007,31(8): 20-29.

[5]Li Hui-liang and Ye Rui-song.Image scrambling and watermarking technique based on 2D cellular automata[J].Journal of Image and Graphics,2008,13(11): 2076-2080.

[6]Li Xiao-wei,Nam Tae-hee,Lee Seok-ki,et al..Digital watermarking in transform-domain based on cellular automata transform[C].2011 The 2nd International Conference on Next Generation Information Technology(ICNIT),China,2011: 132-136.

[7]Wong Peter H W,Chang A,and Oscar A C.Capacity estimation technique for JPEG-to-JPEG image watermarking[J].IEEE Transactions on Circuits and Systems for Video Technology,2003,13(8): 746-752.

[8]Wong Peter H W,Chang A,and Oscar A C.On improving the iterative watermark embedding technique for JPEG-to-JPEG watermarking[C].Proceedings of the 2004 International Symposium,China,2004: 161-164.

[9]Mohammad Amrollahzadeh and Siamak Talebi.A blind JPEG image watermarking in the DCT domain[C].Proceedings of the 18th Conference on Electrical Enqineering(ICEE),Iranian,2010: 311-315.

[10]Koch E,Rinafrey J,and Zhao J.Copyright protection for multimedia data[C].Proceedings of the International Conference on Digital Media and Electronic Publishing,Germany,1994: 321-329.

[11]Jasni Mohamad Zain.Strict authentication watermarking with JPEG compression (SAW-JPEG)for medical images[J].European Journal of Scientific Research,2010,4(2): 232-241.

[12]Lafe O.Cellular Automata Transforms: Theory and Applications in Multimedia Compression,Encryption,and Modeling (Multimedia Systems and Applications)[M].1st Edition,London: Springer,2000: 31-42.