基于重构时间采样的空中机动目标检测与参数估计

吴仁彪 王小寒 李 海 王冬梅

①(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)

②(中国民航西南地区空中交通管理局 成都 610202)

1 引言

机载预警雷达以高空飞行的飞机为载体，具有探测距离远、覆盖范围大、机动灵活等特点。但由于它处于下视工作状态，面临着比地基雷达更复杂的地(海)杂波问题，杂波不仅分布范围广，强度大，而且呈现空时 2 维耦合分布特性，从而导致目标常淹没在强杂波背景中，检测目标能力受到严重影响。STAP是一种有效的机载预警雷达地杂波抑制手段[1,2]，但是传统的STAP方法都是假设在相干处理时间(Coherent Processing Interval,CPI)内目标回波多普勒频率恒定。当来袭目标具有很强的机动性时，其在一个CPI内目标回波多普勒频率随时间发生变化，即发生多普勒走动，使得传统的STAP方法相参积累性能大大下降，从而导致目标检测能力下降[3]。

当机动目标做匀加速运动时，目标回波信号为线性调频(Linear Frequency Modulation,LFM)信号[4]。近年来，基于各种时频分析工具的LFM信号的检测与参数估计方法不断出现[5-11]，包括短时Fourier变换(STFT)[5,6]，小波变换(WT)[5-7]，Wigner-Ville分布(WVD)[5,6]和分数阶Fourier变换(FRactional Fourier Transform,FRFT)[5,6,8-11]等。其中FRFT是1种广义的傅里叶变换方法，它将信号分解在分数阶傅里叶域的一组正交的chirp基上，这就给LFM信号的分析和处理带来了可能性。同时FRFT是一种1维的线性变换，在检测多个机动目标时它不会像WVD那样产生交叉项，而且它的数值计算可借助FFT快速实现，计算简单，易于实现，因此受到了广泛重视。

将FRFT与STAP相结合为空中机动目标的参数估计提供了一条可能的途径。但是，在地基雷达和合成孔径雷达(Synthetic Aperture Radar,SAR)上利用FRFT来估计机动目标参数时都需要较多的脉冲点数[4,12,13]，否则估计精度难以满足要求。由于这个原因，上述方法难以直接应用到机载预警雷达中，因为当雷达脉冲重复频率一定时，较多的脉冲点数意味着CPI加长，这会引起杂波和目标的距离走动，给后续处理带来更大困难[1]。针对上述问题，本文利用干涉SAR中相位展开的思想[14]，提出了基于重构时间采样的空中机动目标检测和参数估计方法，该方法利用空间采样来重构时间采样，等效于增加了单个阵元的时间采样点数，可以提高参数估计精度。仿真实验的结果证明了该方法的有效性。

2 数据模型和问题描述

本文首先给出雷达接收到的数据形式。设机载平台上沿航向方向放置N元均匀线阵，阵元间距为d=0 .5λ,λ为雷达发射脉冲波长，一个CPI内发射K个脉冲。假定单个距离门内最多存在一个目标，则待检测单元的空时快拍可写成

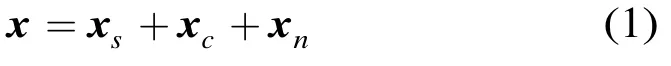
其中xs,xc和xn分别表示目标、杂波和噪声成分。杂波和噪声数据的具体模型见参考文献[3]。

xs表示目标，可表示为如下形式

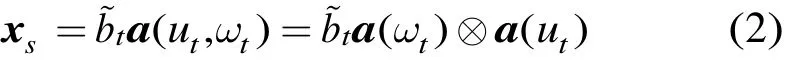
其中为目标回波复幅度，a()为目标空时导向矢量，⊗表示Kronecker积，时域导向矢量a(ωt)=[1,ej2π⋅1⋅fd/fr,…,ej2π⋅(K- 1)⋅fd/fr]T 为K×1维列向量，空域导向矢量a(ut)=[1,ej2π⋅1⋅dcosψt/λ,…,ej2π⋅(N-1)⋅dcosψt/λ]T为N×1维列向量，ψt表示目标来向角，fd表示多普勒频率， (⋅)T表示转置运算。

当目标做匀加速直线运动时，只有目标回波的多普勒频率发生了变化[3]

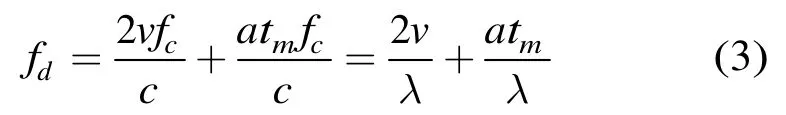
tm表示慢时间，fc为载波频率，v为目标的初始速度，a为目标的加速度，将fd代入到a(ωt)中得到匀加速目标的时域导向矢量为

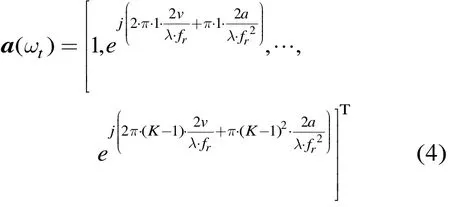
可见，匀加速目标的时域导向矢量部分由两部分组成，分别为目标初始多普勒频率项和调频率项，即当目标做匀加速直线运动时，目标的回波信号为LFM信号。

由杂波分布特性[2]可知：杂波分布范围广，强度大，并且呈现出很强的空时耦合特性，在很大程度上淹没了目标信号，严重影响了雷达对目标信号参数的估计性能。因此，本文的工作可归结为对强杂波背景下的LFM信号的检测和参数估计。

3 空间采样重构时间采样方法

由文献[9]可知，FRFT是一种有效的LFM信号检测和参数估计工具。但是，直接将FRFT应用到机载预警雷达中会产生估计精度较差的问题。基于此，本文利用干涉SAR中相位展开的思想[14]，提出了一种重构时间采样的参数估计方法，即对空间多阵元数据补偿相应相位后进行首尾拼接，该方法等效于增加了单个阵元的时间采样点数，可实现对多个阵元数据的相干积累，提高参数估计精度。本节将从重构时间采样、构造代价函数、解模糊和算法步骤4个部分来重点介绍重构时间采样方法的具体实施过程。

3.1 重构时间采样

当目标做匀加速运动时，对于机载预警雷达的每个阵元来说其回波信号均为一个LFM信号(杂波抑制后)，且每个阵元的LFM信号只差空间相位，如图1(a)所示。因此可以对空间中每个阵元的数据进行相位补偿后首尾拼接，使其等效为增加单个阵元时间采样点数的效果，如图1(b)所示。不失一般性，下面以两个阵元为例讨论将多阵元首尾拼接时每个阵元所需补偿的相位。

由第2节的目标数据模型可知，当不考虑空间相位时，两个阵元接收到的目标数据为

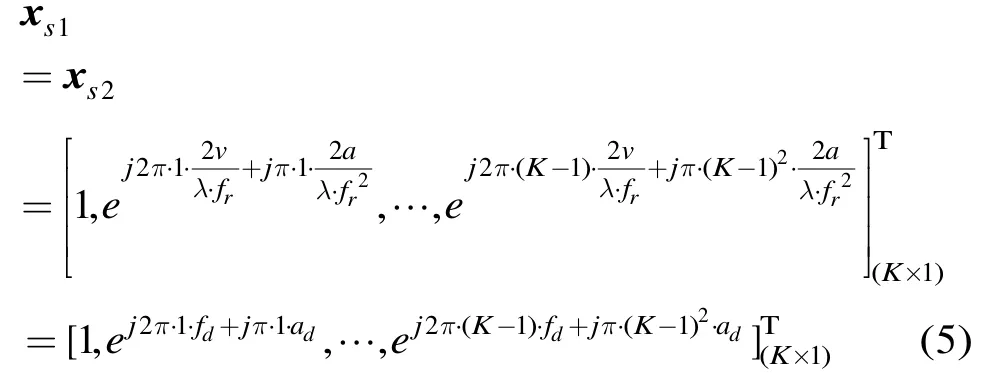
其中xs1表示第1个阵元接收到的目标信号，xs2表示第2个阵元接收到的目标信号，K为脉冲点数，fd=2v/λfr为初始频率，ad=2a/λfr2为调频率，λ为波长，fr为脉冲重复频率。

当一个阵元的时间采样点数由K增加到2K时，该阵元接收到的目标信号为

其中⊙为Hadamard积。由此可见，对第2个阵元的数据进行相位补偿后再跟第1个阵元的数据拼接就可以等效为一个阵元直接增加时间采样点数的效果。

由式(6)可以得出对第2个阵元应该补偿的相位为

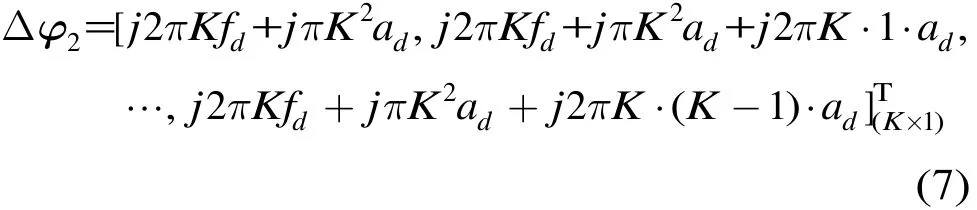
同理，第n个阵元应该补偿的相位为

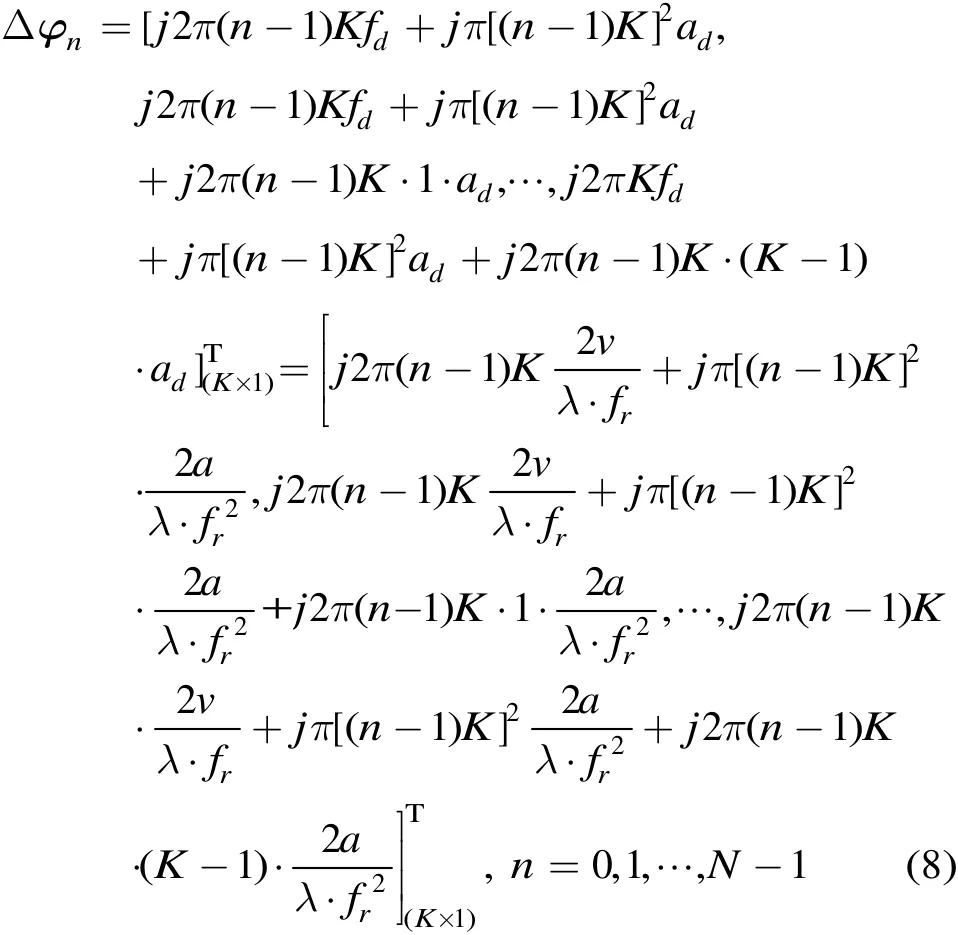
这样，将每个阵元接收到的数据分别补偿其相对应的相位(参考阵元除外)后进行首尾拼接，此时再进行FRFT变换，相当于对所有数据进行相干积累，因此积累后的目标能量大大提高，估计精度更好。

3.2 构造代价函数

然而，由上述分析可知：每个阵元所需补偿的相位中又包含了未知的目标参数，导致无法直接对多个阵元进行数据拼接。由于FRFT是线性变换，能够对LFM信号进行能量积累，因此可以构造一个参数搜索区间，对此区间内的每组参数进行多阵元拼接后做FRFT变换，当拼接效果最好时能量积累最大，所以取每组参数拼接后数据做FRFT变换后的能量最大值作为代价函数，只需通过搜索代价函数的最大值就可以得到参数的估计结果。为减小计算量，本文对拼接后的数据进行Zoom-FRFT变换[15]，即根据需要选择变换输出的局部谱区域，求得变换后的能量最大值。Zoom-FRFT变换缩短了2维搜索的区域，因此减小了计算量。所以，在参数搜索区间内构造代价函数为

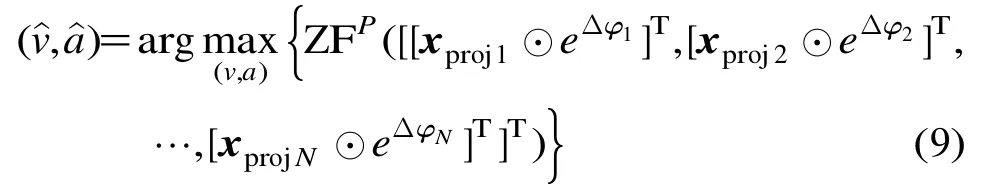
其中xprojn为第n个阵元杂波抑制后数据，Δφn为第n个阵元所需补偿的相位，见式(8)，[[xproj1⊙个阵元数据进行重构时间采样(NK×1维列向量)，ZFP[⋅]为Zoom-FRFT的算子符号。这样当搜索到目标真值时，阵元拼接效果最好，能量积累最大，所以求其峰值对应的参数即为目标参数(证明略)。

3.3 解模糊方法

但是由式(8)可以看出：每个阵元所需的补偿项存在周期性变化，这样就导致估计结果会产生模糊，因此需要对其进行解模糊处理，进一步精确参数搜索区间。不失一般性，以两个阵元为例具体分析估计结果产生模糊原因以及解模糊方法。

首先以单频信号为例，即加速度项为零，此时第2个 阵 元 应 该 补 偿 的 项 为[ej2πKfd,ej2πKfd,…,，对初始速度进行搜索，其代价函数如图2所示，正是由于补偿项ej2πfd K为一个周期函数，导致参数搜索的代价函数也会呈现周期性变化，其周期满足：=2v⋅K/λfr=N，即速度非模糊最小周期为vp=λfr/(2K)，带来的结果就是如果不能正确地确定搜索区间，就有可能搜索到其他区间的峰值，产生模糊，导致误差很大，所以就要对其进行解模糊。

当估计结果产生模糊时，模糊值和真值的关系为

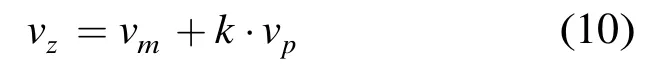
其中vz为理论真值，vm为搜索到的模糊值，vp为周期，k为整数。由于其周期性由K决定，所以可以通过取不同的K值来解模糊，如式(11)表示

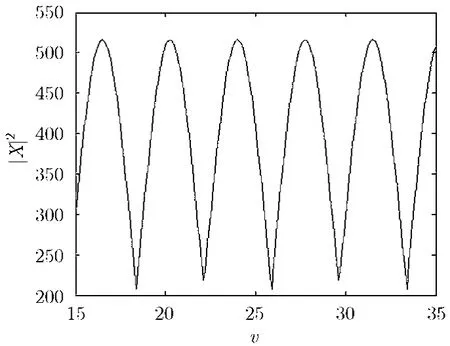
图2 初始速度参数搜索代价函数示意图

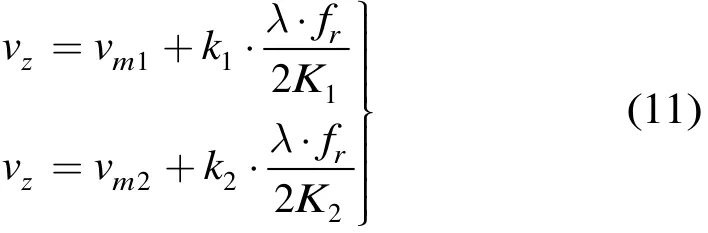
通过取不同的K值，求解此方程组，k1,k2取整数，即可求得vz，确定理论真值所在的区间。

当含有加速度时，第2个阵元的补偿项为

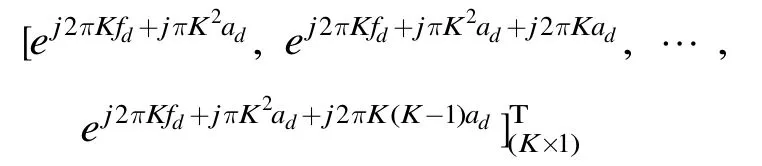
3.4 算法步骤

图3为本文所提基于重构时间采样方法估计机动目标参数的流程图。具体步骤如下：

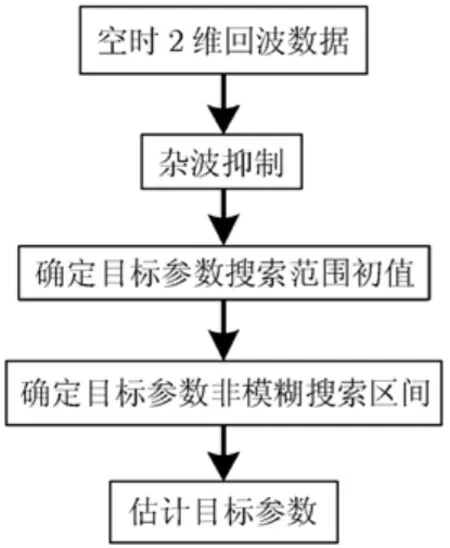
图3 本文方法实现框图

第1步 杂波抑制 本文通过子空间投影技术进行杂波抑制，详细过程在此不再叙述，请参考文献[16]中步骤1。

第2步 确定目标参数搜索范围初值 由第1步可知，杂波抑制后的数据可表示为

分别对杂波抑制后的每个阵元数据进行FRFT变换，然后再对结果进行非相干积累，如式(13)所示。

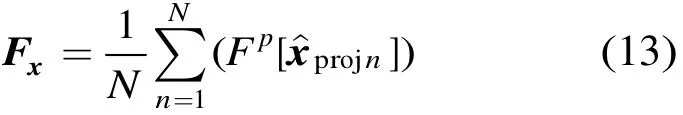
其中为利用估计协方差矩阵抑制杂波后第n个阵元的数据，N为阵元数。

搜索得到非相干积累能量最大时的速度和加速度为

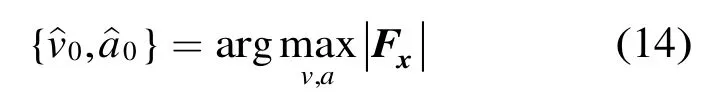
该步搜索参数的初值也可通过快速解线调的方法来确定[3]。

第3步 确定目标参数非模糊搜索范围 由4.3节的分析可知，需要对参数搜索范围进行解模糊处理。选取不同的脉冲采样点数K1和K2，确定一个参数搜索范围，初始速度的搜索范围取5倍于其非模糊周期的范围，加速度的搜索范围可根据先验信息选取，如空空导弹已经可以达到100g的机动过载，F-22战斗机也有5g以上的超音速机动能力等[4]。通过式(9)分别估计结果和，再根据式(11)来进行解模糊处理

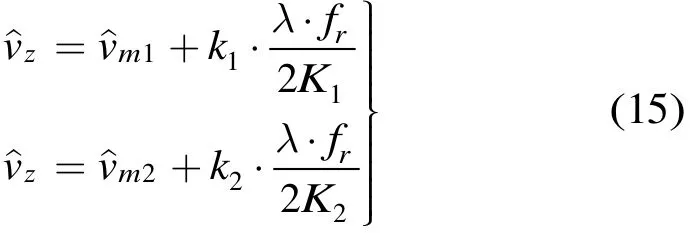
第4步 估计目标参数 此时再根据式(9)在第3步得到的参数非模糊搜索范围内构造代价函数

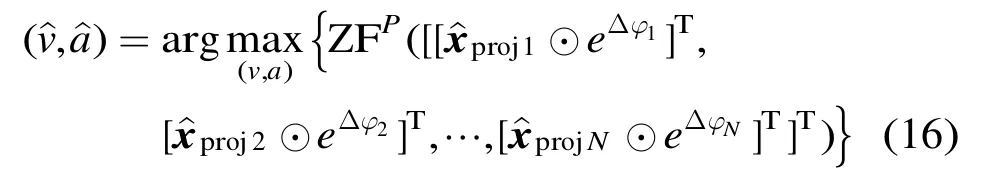
求得代价函数最大值所对应的参数，即可得到估计结果。

4 仿真分析

仿真参数设置：天线阵为阵元数N=16的正侧视理想均匀线阵，阵元间距d=0.5λ。载机速度为120 m/s，雷达工作波长为0.32 m，平台高度为10 km，雷达距离分辨率为20 m，脉冲重复频率为1500 Hz，相干处理脉冲数K=64，输入信噪比SNR=0 dB，杂噪比CNR=50 dB。机动目标处于检测单元内，处于方位角90°处，初始速度为24.01 m/s，加速度为299.9 m/s，实验中假设目标方位已知，该实验中估计参数均方根误差均进行了200次蒙特卡罗实验。

图4所示为杂波抑制前的功率谱，由于信杂比很低，信号完全被淹没在杂波中。图5为杂波抑制后的功率谱，可以看出杂波被抑制掉了，目标突显出来，由于目标存在加速度，其在多普勒域存在一定的展宽。

图6为不同方法能量积累效果图，图6(a)为对单个阵元进行FRFT变换的结果，图6(b)为对每个阵元的数据进行FRFT变换后进行非相干积累的结果，图6(c)为利用本文方法处理后进行FRFT的结果。通过比较可以看出，图6(a)中由于只利用了单个阵元的数据进行变换，所利用脉冲点数较少，因此积累后目标能量很微弱，在图中很难检测到目标。图6(b)中虽然利用了多个阵元的数据，但由于是非相干积累，因此改善能力有限，仍然无法对目标进行很好的检测。图6(c)中由于利用空间采样来重构时间采样的方法拼接等效成一个阵元的数据后进行FRFT变换，相当于利用多个阵元的数据进行相干积累，因此积累后的目标能量大大提高，能够很好地进行目标检测和估计。

不同方法估计结果的均方根误差如表1所示，可见本文方法的参数估计结果精度最高。

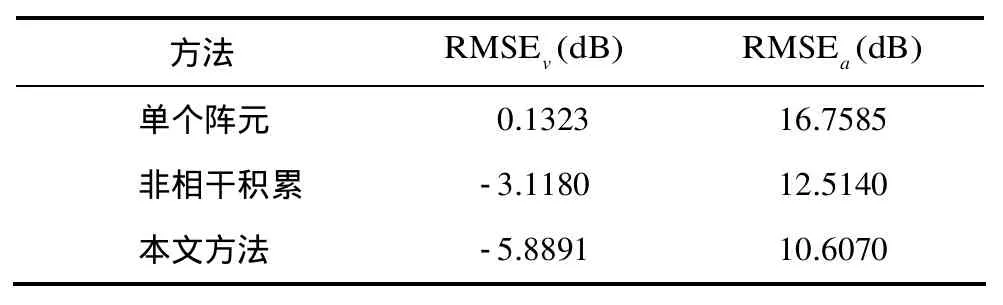
表1 不同方法估计结果比较表

图7为3种方法估计得到的参数均方根误差与CRB界的比较结果图(机载雷达机动目标参数估值的CRB推导过程略)，其中图7(a)为初始速度均方根误差与CRB界的比较结果图，图7(b)为加速度均方根误差与CRB界的比较结果图。可以看出本文方法估计性能最接近CRB界，估计效果最好，尤其在低信噪比的情况下，其优势更加明显。

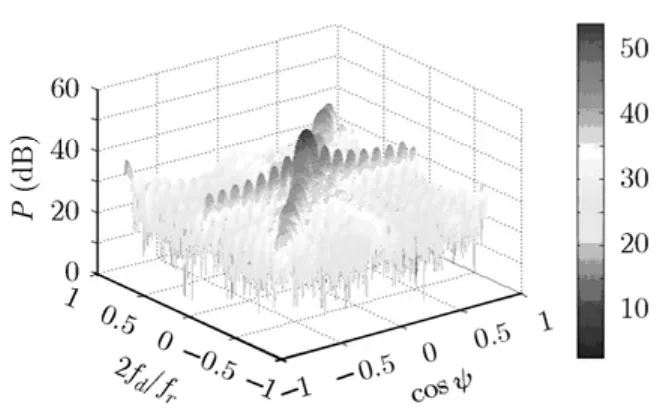
图4 总回波的功率谱

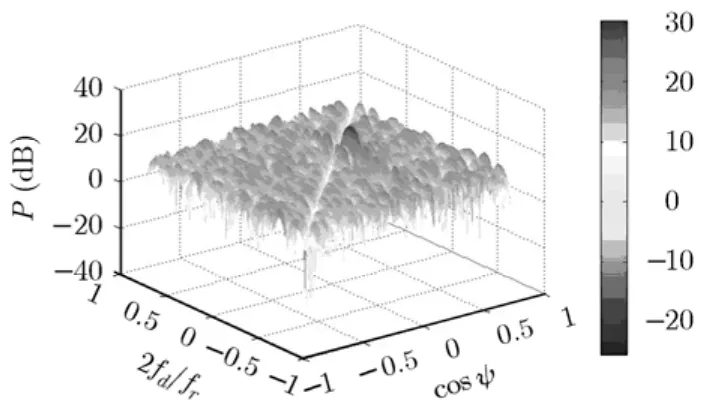
图5 杂波抑制后的功率谱

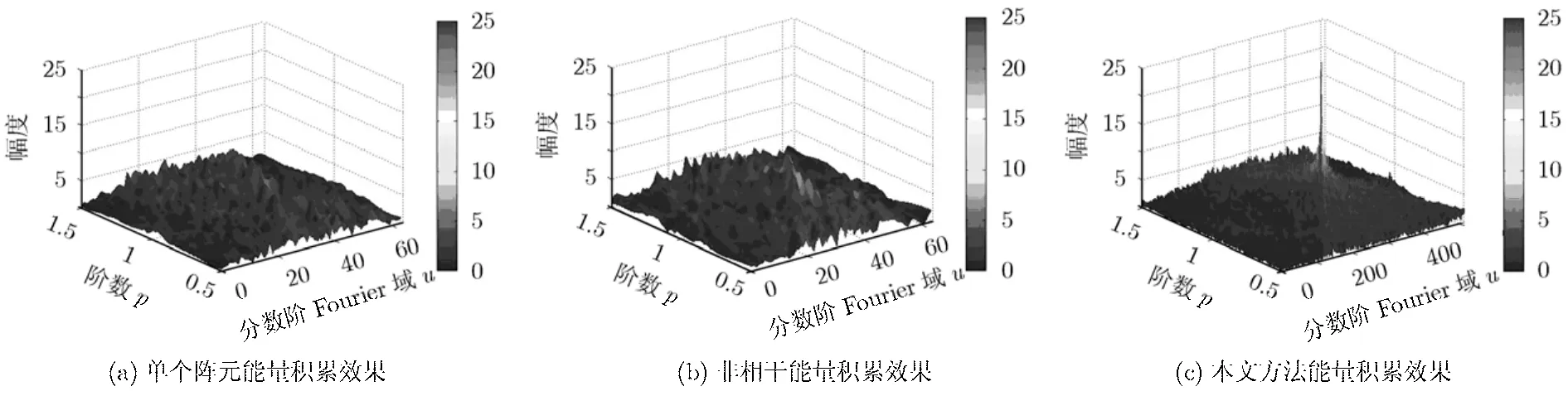
图6 不同方法能量积累效果图

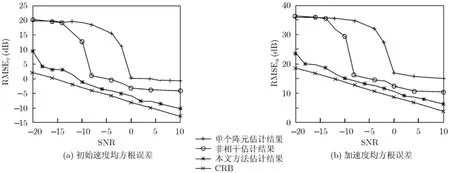
图7 参数均方根误差随信噪比变化曲线

表2给出了本文算法中各个步骤所需运算量，其中Ns为估计协方差矩阵所需样本数，prg表示做FRFT变换时阶数p的搜索范围[pc,pz],pc和pz为该范围的初值和终值，Δp为阶数p的搜索步长，vrg表示初始速度的搜索范围[vc,vz],vc和vz为该范围的初值和终值，Δv为初始速度搜索步长，arg表示加速度的搜索范围[ac,az],ac和az为该范围的初值和终值，Δa为加速度搜索步长，K1和K2为解模糊时选取的不同脉冲点数，Nc为该方法中所需拼接的阵元数。

5 结束语

本文提出了一种基于重构时间采样的空中机动目标检测和参数估计方法，该方法能够在脉冲点数有限的情况下得到准确的目标参数估计结果。文中将该方法的估计结果与直接应用FRFT变换的估计结果进行了比较，同时给出了其与CRB界比较的结果，可以看出，该方法的估计性能较之其它方法有了显著的提高。

表2 本文算法中各个步骤所需运算量分析结果

[1]Klemm R.Principle of Space-Time Adaptive Processing[M].3rd Edition,UK,IET Publishers,2006: 1-100.

[2]王永良,彭应宁.空时自适应信号处理[M].北京: 清华大学出版社,2000: 26-45.Wang Yong-liang and Peng Ying-ning.Space-Time Adaptive Processing[M].Beijing: Tsinghua University Press,2000:26-45.

[3]王冬梅.基于STAP的空中机动目标检测研究[D].[硕士论文],中国民航大学,2010.Wang Dong-mei.Study on space time adaptive maneuvering target detection technology[D].[Master dissertation],Civil Aviation University of China,2010.

[4]刘建成.加速运动目标检测及跟踪技术研究[D].[博士论文],国防科学技术大学,2007.Liu Jian-cheng.Study on accelerating target detection and tracking[D].[Ph.D.dissertation],National University of Defense Technology,2007.

[5]张贤达,保铮.非平稳信号分析与处理[M].北京: 国防工业出版社,1998: 12-284.Zhang Xian-da and Bao Zheng.Analysis and Processing of Nonstationary Signal[M].Beijing: National Defense Industrial Press,1998: 12-284.

[6]唐向宏,李齐良.时频分析与小波变换[M].北京: 科学出版社,2008: 45-136.Tang Xiang-hong and Li Qi-liang.Time-Frequency Analysis and Wavelet Transform[M].Beijing: Science Press,2008:45-136.

[7]Li Liang-chuan.A new method of wavelet transform based on FFT for signal processing[C].WRI Global Congress on Intelligent Systems,Wuhan,2010: 203-206.

[8]Pei Soo-chang and Ding Jian-jiun.Fractional Fourier transform,Wigner distribution,and filter design for stationary and nonstationary random processes[J].IEEE Transactions on Signal Processing,2010,58(8): 4079-4092.

[9]陶然,邓兵,王越.分数阶傅里叶变换以及应用[M].北京: 清华大学出版社,2009: 12-49.Tao Ran,Deng Bing,and Wang Yue.Fractional Fourier Transform and Its Applications[M].Beijing: Tsinghua University Press,2009: 12-49.

[10]Qi Lin,Tao Ran,Zhou Si-yong,et al..Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J].Science in China Ser.F Information Sciences,2003,33(8): 749-759.

[11]Zhao Fen-xia and Zhai Xin-duo.The algorithm and error analysis of fractional Fourier transform[C].International Conference on Information Engineering and Computer Science,Wuhan,2010: 1-4.

[12]孙泓波,顾红,苏卫民,等.利用分数阶Fourier域滤波的机载SAR多运动目标检测[J].航空学报,2002,23(1): 33-37.Sun Hong-bo,Gu Hong,Su Wei-min,et al..Using the filtering in fractional Fourier domain for airborne SAR multiple moving targets detection[J].Acta Aeronautica Et Astronautica Sinica,2002,23(1): 33-37.

[13]胡海荣.基于分数阶Fourier变换的合成孔径雷达动目标检测方法[D].[硕士论文],浙江工业大学,2009.Hu Hai-rong.The SAR moving targets detection based on fractional Fourier transform[D].[Master dissertation],Zhejiang University of Technology,2009.

[14]李海,廖桂生.对配准误差稳健的多基线相位展开方法[J].电子学报,2008,36(9): 1670-1675.Li Hai and Liao Gui-sheng.A robust phase unwrapping method to coregistration error for multiba seline InSAR systems[J].Acta Electronca Sinica,2008,36(9): 1670-1675.

[15]赵兴浩,陶然,邓兵,等.分数阶傅里叶变换的快速计算新方法[J].电子学报,2007,35(6): 1089-1093.Zhao Xing-hao,Tao Ran,Deng Bing,et al..New methods for fast computation of fractional Fourier transform[J].Acta Electronca Sinica,2007,35(6): 1089-1093.

[16]吴仁彪,贾琼琼,李海.机载雷达高速空中微弱动目标检测新方法[J].电子与信息学报,2011,33(6): 1459-1464.Wu Ren-biao,Jia Qiong-qiong,and Li Hai.Detection of fast moving dim targets on airborne radar via STAP[J].Journal of Electronics＆Information Technology,2011,33(6):1459-1464.