提供QoS保障的无线多跳路径可用带宽估计模型与方法

宋 安 赵海涛 王 杉 魏急波

(国防科技大学电子科学与工程学院 长沙 410073)

1 引言

无线多跳自组网能为布线困难的环境提供快速便捷的网络服务，在军事和民用两方面均得到广泛应用。作为其基本构成单位，无线多跳路径具备多跳网络的两个基本特征，即流内竞争与节点负载间存在依赖关系，因此对多跳路径的研究构成了研究多跳自组网的基础。

为了给在网络中占据了越来越大比重的QoS敏感业务提供更好的服务，对网络剩余通信能力即可用带宽的研究得到了极大的关注。可用带宽的定义为：在不影响网络中所有业务流的QoS的前提下，网络能支持的最大额外负载。但是现有的可用带宽估计方法中，基于测量的方法[1]和基于感知的方法[2-4]均将网络所能支持的最大吞吐量作为可用带宽，而没有考虑估计结果被使用后会给网络带来何种影响；基于模型的方法能在估计过程中考虑业务流之间的相互影响，但是文献[5]仅考虑了业务流的MAC层干扰约束而不能为业务提供QoS保障。

设计基于分析模型的可用带宽估计方法的前提是建立一个满足需要并且准确可靠的多跳路径分析模型。该模型必须具备以下两个特点：第一，必须全面考虑流内竞争带来的影响；第二，必须能够体现路径性能随外部负载的变化关系。但是在现有的研究中，针对流内竞争的研究不够全面，他们要么假设了理想调度而忽略了节点的相互干扰[6]，要么在进行碰撞分析时仅考虑隐藏节点的影响，而忽略了邻节点间的冲突[7-9]。此外，这些研究大多假设网络处于饱和状态，没有研究节点负载间的关系以及外部负载对网络性能的影响。

针对现有研究工作的不足，本文对多跳路径的干扰问题进行了详细分析与定量计算，并建立了基于排队网络理论的多跳路径性能分析模型；基于该分析模型，以业务流的时延、丢包率与吞吐量等QoS需求不被破坏为约束条件设计了多跳路径的可用带宽估计方法；通过仿真实验，验证了分析模型的准确性与可用带宽估计方法的合理性。

2 多跳路径上的干扰分析

2.1 系统模型与假设

考虑由N+1个运行 IEEE 802.11协议的静止节点组成的N跳路径。为了便于分析，假设理想信道并且所有节点具有相同的MAC层与物理层参数。根据 NS2仿真器的默认值，设置节点的传输范围RTX为250 m，载波侦听范围RCS为550 m，捕获门限为 10 dB。根据参考文献[7]的场景设置，取邻节点间距d为200 m。典型的多跳路径如图1所示。

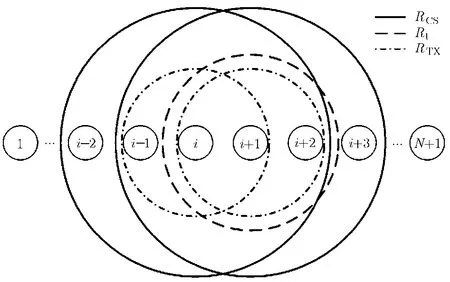
图1 典型的多跳路径示意图

对于节点i，其干扰范围RI是指落在其内的竞争节点会影响i的接收，即出现碰撞的区域。利用文献[10]中的干扰范围计算方法，可得出当捕获门限为10 dB时，RI为356 m。为了简化分析，假设节点工作于基本访问模式，这是因为在多跳网络中，当RCS大于两倍RTX时，RTS/CTS机制并不能有效地消除隐藏节点问题[10]。

2.2 干扰的定性分析

与流间竞争不同，流内竞争是多跳网络的特有现象。多跳路径只存在流内竞争，这是影响路径中业务流性能和路径可用带宽的关键因素。流内竞争体现为路径上节点间的相互干扰，我们针对图1中由发送节点i与接收节点i+1构成的链路(i,i+1)对干扰进行分类分析。

(1)对退避过程的干扰：对于正在退避的节点i，其RCS范围内的干扰会影响i的退避过程，具体表现为若i感知到RCS范围内信道忙，会挂起其退避过程，直到信道恢复空闲后才继续退避。令CS(i)表示节点i的RCS范围内节点的集合，由于载波侦听范围与节点间距满足关系 2d＜RCS＜ 3d，因此有CS(i)={i± 2,i± 1 }。

(2)来自邻节点的同步碰撞：同时位于i的RCS范围与i+1的RI范围之内的节点与i在同一时隙进行发送时，会与i的发送发生碰撞，这样的碰撞称为同步碰撞。令SynN(i)表示对链路(i,i+1)造成同步碰撞的节点的集合，那么SynN(i)={i+ 1,i+ 2 }。

(3)来自隐藏节点的异步碰撞：链路(i,i+1)的隐藏节点是指位于i的RCS范围之外但是i+1的RCS范围之内的那些节点，即节点i+3。若i+3向i+ 4 的传输早于i向i+1的传输，且在i开始传输时i+3的传输尚未结束，那么i+1检测到信道忙从而不会对i的发送进行应答，于是i便认为此次传输出现碰撞。但是，若i+3的传输晚于i的传输，捕获效应使得i+3不会干扰(i,i+1)上的传输。隐藏节点造成的碰撞不要求隐藏节点与发送节点的传输同时进行，因此称为异步碰撞。令HN(i)表示(i,i+1)的隐藏节点的集合，那么HN(i)={i+ 3 }。

2.3 干扰的定量计算

对多跳路径上的干扰进行建模分析时，必须考虑非饱和状态以及异构业务源。这是因为：(1)只有在非饱和条件下路径上才存在可用的剩余带宽；(2)路径上任意节点都可能有业务流加入或离开网络，并且节点的输入还依赖于其上游节点的输出。

非饱和条件下的尝试速率可使用队列利用率ρ对饱和条件下的尝试速率进行松弛来获得。根据文献[11]提出的不动点方法，饱和时节点的尝试速率为发送一个报文的平均尝试次数与平均退避时隙数之比，因此非饱和状态时的尝试速率为

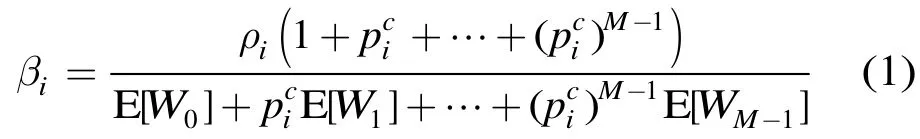
其中下标i表示第i个节点，为条件碰撞概率，ρi为队列利用率，M为最大重传次数。退避阶段j的退避窗口Wj服从离散均匀分布，其均值与方差分别为

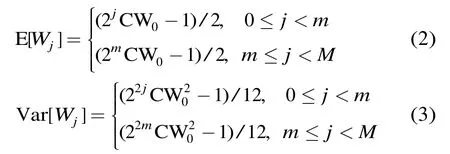
其中CW0是初始竞争窗口，m是最大退避阶段。

其中，邻节点导致的同步碰撞概率为

根据2.2节的分析，若隐藏节点的传输早于该链路上的传输且领先的时间不超过报文的传输时间，那么碰撞就会发生，该时间区域称为链路的脆弱期。对于基本访问模式，链路的脆弱期V等于报文传输时间加上短帧间间隔SIFS，即

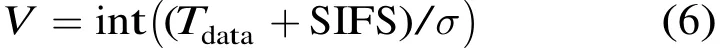
其中Tdata表示报文传输时间。V是以系统时隙长度σ为单位的整数值，int(⋅)表示取整操作。注意到隐藏节点只有在处于退避过程时的那段脆弱期才可能因发送报文而引起碰撞。令表示节点j花在非挂起状态的退避过程中的平均时间，并令其平均服务时间为E[Tst,j]，那么j有报文传输且处于非挂起状态的退避过程的概率为bj/E[Tst,j]，于是隐藏节点在链路脆弱期的任意时隙进行发送而造成异步碰撞的概率为

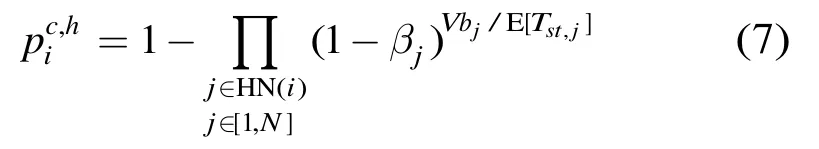
给定节点队列利用率ρi，式(1)，式(2)和式(4)构成了DCF机制的不动点方程组，并可通过数值计算求解每个节点的碰撞概率。我们将在第 3.3节利用排队网络理论对ρi进行讨论。

最后，节点i检测到RCS范围内信道变忙从而导致退避过程被挂起的概率为

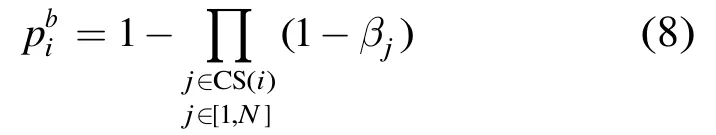
3 排队网络模型

假设路径上存在K个流，每个流均发送长度为L的等长报文，其中第k个流的起始节点为sk，终止节点为dk，平均输入速率为且服从泊松分布。节点具有无限长队列。令F(K)表示所有流的集合，N[sk,dk]表示流k所经过的节点集合，FSRC(i)表示以节点i∈[1,N]为源节点的流的集合，FDST(i)表示以节点i∈[2,N+ 1]为目的节点的流的集合。于是无线多跳路径可建模为开放排队网络，并可通过扩散近似法来分析这K个流各自的QoS参数。

3.1 扩散近似法

扩散近似法[12]可用来求解开放 G/G/1排队网络。考虑由N个节点构成的排队网络，其外部输入负载是一个更新过程，报文到达间隔的平均值与变异系数分别为1/λe与cA。令节点i的服务时间的均值与变异系数分别为1/μi与cBi。定义排队网络中节点的访问率为一个报文被该节点转发的平均次数，那么节点i的访问率ei为

其中p0i表示报文经由节点i进入网络的概率，pji表示报文在节点j服务完毕后转发到节点i的概率。到达节点的报文包括节点自己产生的报文和其他节点转发的报文，因此我们用有效到达速率λi来表示实际到达节点i的报文速率。

节点i的队列利用率ρi可表示为

节点i的报文到达间隔时间的平方变异系数可以近似表示为

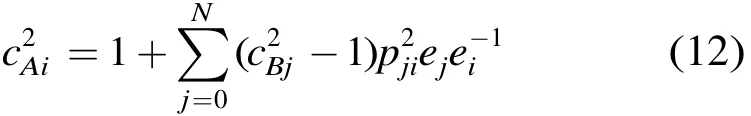
其中

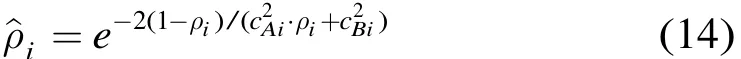
于是节点i队列中的平均报文数为

3.2 排队网络的参数

为了能够使用扩散近似法来求解排队网络，我们需要将扩散近似法所需的参量表示为多跳路径的网络参数。

引理 1 在处于稳定状态的多跳路径上，报文在节点i服务完毕后转发到节点j的路由概率为

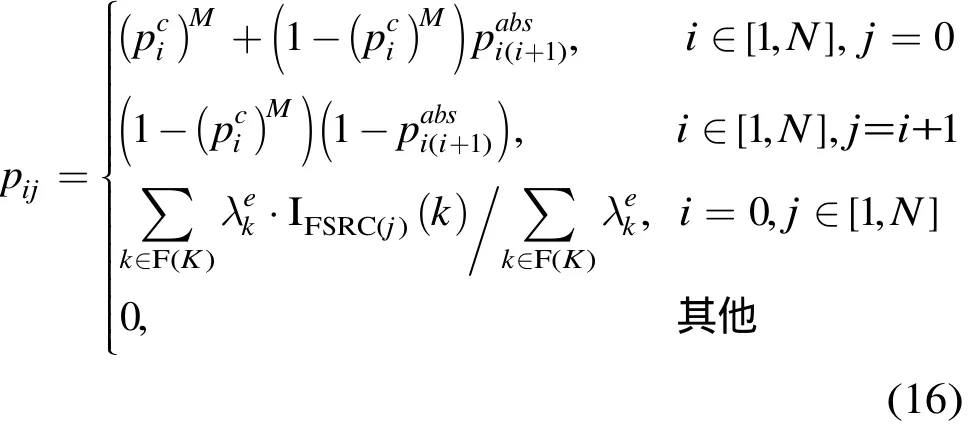
其中pi0表示报文在节点i处理完毕后离开网络的概率；I(x)为指示函数；为链路(i,i+1)的吸收

A概率即i的所有输出报文中，因i+1是目的节点而在i+1离开网络，从而不会进入i+1的队列的概率，且

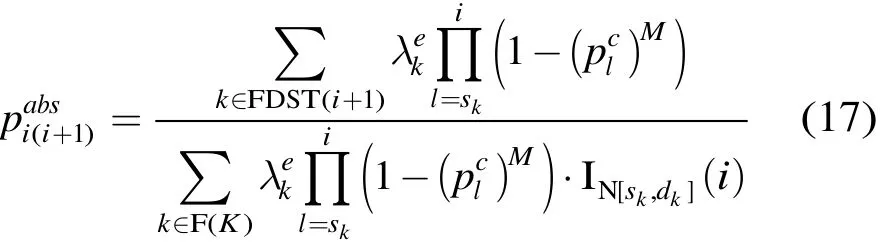
证明 稳定状态时，节点i输出报文的聚合速率为所有经过i的流在此之前所经过的节点中未因超过重传限制而损失的速率之和，即式(17)的分母。而分子表示因i+1是目的节点而离开网络的流的聚合速率，后者与前者之比即链路(i,i+1)的吸收概率。i的输出报文离开网络的原因包括：(1)以概率在i处因超过重传限制而被丢弃；(2)在i处没有被丢弃但是i+1是目的节点，其概率为于是报文在i处理完毕后离开网络的概率为

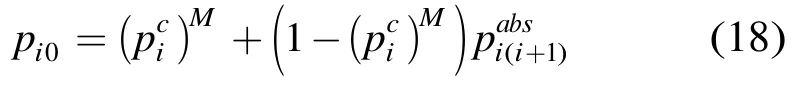
受路径拓扑限制，i的报文只能直接传输给i+1，于是报文由i转发给i+1的概率为

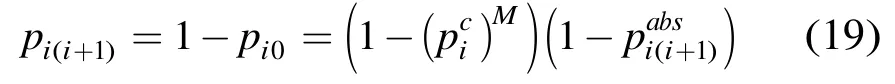
报文在节点j处进入网络的聚合速率可表示为整个路径的外部输入负载的聚合速率者之比即报文经由j进入网络的概率为

联立式(18)~式(20)即得式(16)。 证毕

引理 2 稳定状态时，多跳路径中节点的访问率由式(21)给出

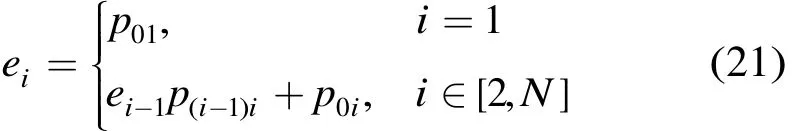
证明 路径的源节点只有来自排队网络外部的输入，因此e1=p01；而路径上的其他节点的输入除了可能的外部输入外，还包括来自上一跳节点输出，因此通过节点访问率的相互关系式(9)容易得出证毕

引理3 稳定状态时，节点i的有效到达速率λi为

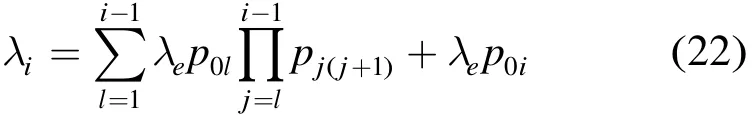
证明 根据访问率的定义式(10)，即λi=λeei，反复运用引理2中的式(21)即得式(22)。 证毕

定理 1 当输入负载均服从泊松分布时，节点的报文到达间隔时间的SCV为

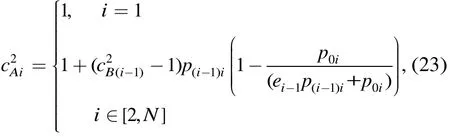
证明 由于泊松流的合成仍为泊松流，因此任意节点i的外部输入服从参数为的泊松分布。根据泊松分布的性质，i的外部输入过程的报文到达间隔时间服从负指数分布，其均值与方差均为 1 /λe,i，因此其 SCV 为由于路径源节点只有来自排队网络外部的输入，根据式(12)，可计算源节点的报文到达间隔时间的SCV为

而对于路径上的其他节点，利用引理2的结论可得其报文到达间隔时间的SCV为

联立式(24)与式(25)即得式(23)。 证毕

3.3 服务时间的平方变异系数

服务时间是指报文从到达队首到其离开队列为止之间的时间间隔，而不管报文是否成功传输到目的节点。为了符号表示方便，除非特别说明，本节省略代表节点i的下标。令Tst_s表示成功传输的报文的服务时间，受文献[13]的启发，可计算Tst_s的均值和方差分别为

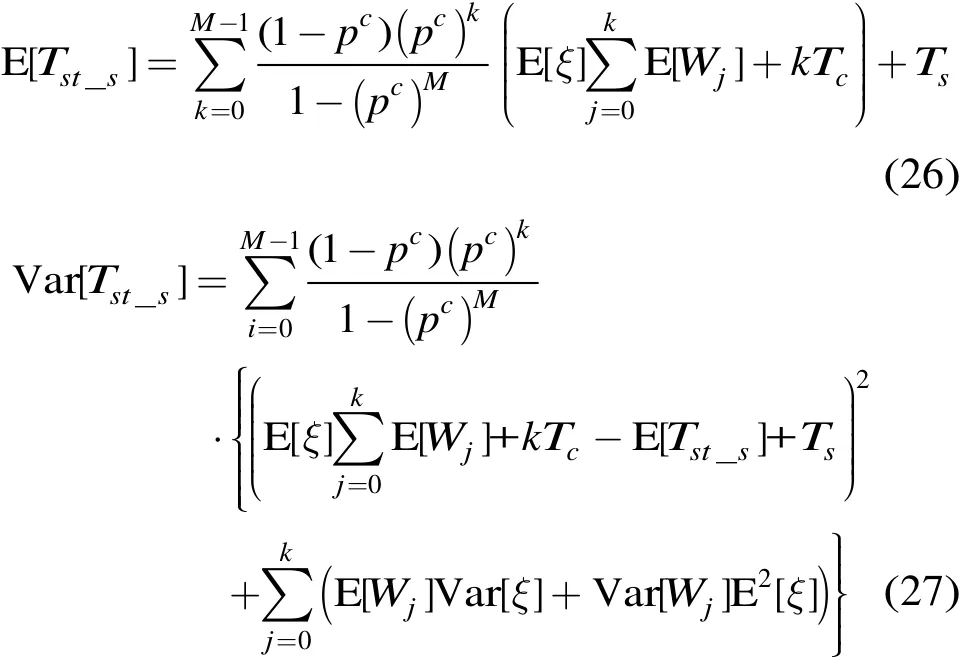
其中Ts与Tc分别为报文成功传输与发生碰撞的时间，E[Wj]与Var[Wj]分别由式(2)和式(3)给出。ξ代表节点在每个退避时隙实际花费的时间，由于节点检测到其RCS范围内信道变忙的概率为pb(见式(8))，于是有

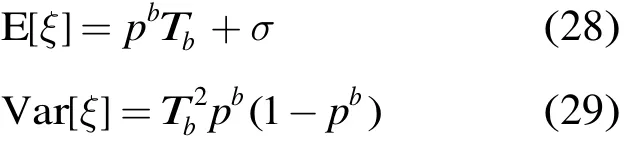
类似地，令Tst_d表示因超过重传限制而丢弃的报文的服务时间，有

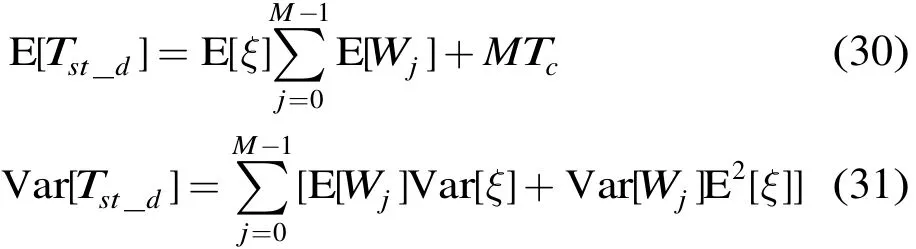
于是，节点i发送报文的服务时间的SCV为

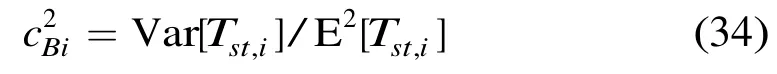
节点i的队列利用率为

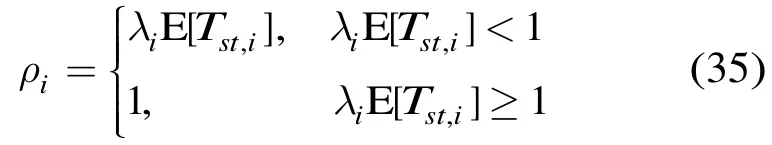
3.4 多跳路径中业务流的QoS参数

根据Little定律，报文在链路(i,i+1)的平均时延为那么流k的平均时延，即其经过的链路的时延之和为

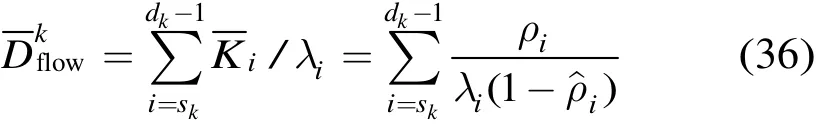
在无限队长与理想信道假设下，超过重传限制是报文丢弃的唯一原因。由于当报文在其经过的每跳链路上都不被丢弃时才能成功传输到目的节点，因此流k的丢包率为

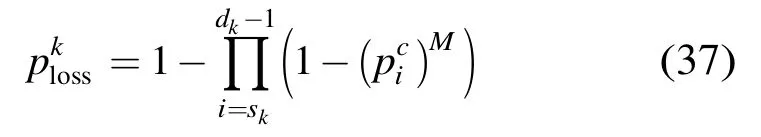
对于链路(i,i+1)，吞吐量Si等于单位时间内所有在i服务完毕而离队的报文中成功传输到i+1的报文数。当i非饱和时，报文的平均到达速率小于平均服务速率，所有报文均接受 MAC层的服务，吞吐量依赖于负载的大小；而当i饱和后，吞吐量只受其服务时间的约束。由于式(10)只适用于稳定状态下的排队网络，因此引理3不能反映饱和状态时节点负载间的关系。例如，当i-1饱和后，其输出不再依赖输入，而此时i的负载中来自i-1的部分受制于其服务速率。注意到无论i-1是否饱和，其向i的输出都是其吞吐量Si-1，于是用式(38)的递推式来计算链路(i,i+1)的吞吐量：

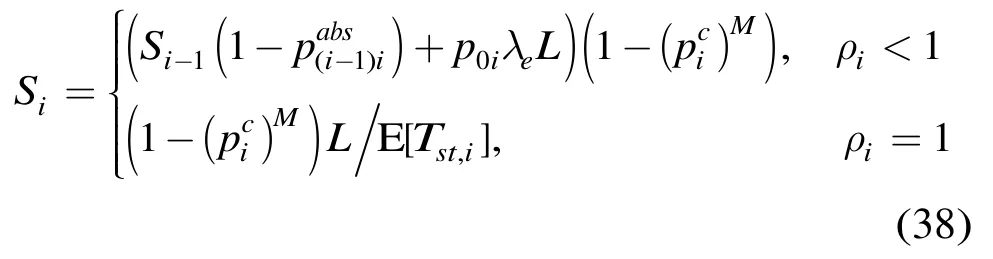
其中S0=∑k∈FSRC(1)λe为路径源节点的聚合输入负载。经过链路(i,i+1)的流k在(i,i+1)上的输入速率等于其在上一跳链路的吞吐量。如果i非饱和，那么该流在(i,i+1)的吞吐量是其输入速率中不被丢弃的部分；反之，若i饱和，那么等于在(i,i+1)的饱和吞吐量中，属于流k的输入速率占所有进入i的队列的输入速率的比例。即

注意式(39)中i∈[s,d- 1],代表流k的

kk外部输入速率。而流k的吞吐量Sk就等于它经过最后一跳链路时的吞吐量，即

4 可用带宽估计原则与方法

根据可用带宽的定义，给定带宽可用的前提是该带宽被使用后网络中所有业务流的QoS不能受到破坏。于是判断给定带宽是否可用，或者说判定带宽需求的可行性，可转变为首先通过网络分析模型计算带宽需求被满足后所有业务流的QoS参数，然后将这些参数与预先定义的门限值进行比较，如果所有参数都不超过其门限值，那么认为QoS不会受到影响，于是判定该带宽需求可行；否则，如果任何一个参数超过了门限值，那么判定该带宽需求不可行。在本文的分析中，我们使用时延，丢包率与吞吐量这3个被广泛接受的QoS度量。令λAB表示带宽需求，于是求路径的可用带宽转变为式(41)所示的非线性规划问题

其中LossThd与DelayThd分别表示业务能容忍的最大丢包率与最大端到端时延，与分别表示在所需求的带宽被使用前与使用后流k的吞吐量，ThpDegThd为业务能容忍的最大归一化吞吐量跌幅，最后一个约束意味着当所需求的带宽被使用后，路径中之前已经存在业务流各自的吞吐量归一化跌幅不能超过门限值ThpDegThd。

上述非线性规划问题很难求出闭合解，但是考虑到 802.11网络具有下述性质[14]：如果带宽需求λAB可行(即满足式(41)中的约束)，那么所有小于λAB的需求也可行；反之，若λAB不可行，那么所有大于λAB的需求也不可行。于是可通过尝试的方法，逐步增大λAB来寻找不破坏QoS约束的最大带宽需求。我们采用具有对数复杂度的二分查找法以减少搜索次数。当相邻两次搜索结果小于规定的精度时，搜索过程结束，此时的λAB即为路径的可用带宽。

5 仿真验证

通过数值分析与NS2仿真实验来验证本文提出的分析模型和可用带宽估计方法。数值分析和仿真均采用IEEE 802.11b的标准设置，数据速率为11 Mbps。采用 NOAH静态路由协议以避免动态路由协议带来的干扰。

我们在6跳路径中采用不同的场景配置来验证本文提出的可用带宽估计原则。设置报文长度为1024 byte,QoS约束为单向时延不超过150 ms且丢包率不超过0.5%。场景1：当100 kbps的背景流只经过路径中第3与第4跳链路时分析经过整个路径的目标流的带宽需求的可行性。从图2(a)中可以看出，当带宽需求达到1.06 Mbps后，目标流的时延约束首先被打破，因此只有小于1.06 Mbps的带宽需求才是可行的。场景2：当100 kbps的背景流经过整个路径时分析只经过第2至第4跳链路的目标流的带宽需求的可行性。图2(b)中，随着带宽需求的增加，首先被打破的是背景流的丢包率约束，因此只有小于1.55 Mbps的带宽需求才是可行的。而由图2(c)可以看出，在目标流的吞吐量达到其最大值之前，背景流的丢包率已经超过了0.5%，这说明目标流的可用带宽小于其最大可达吞吐量。以上事实也证明了文献[1-5]的估计方法不够准确，因为他们仅考虑了吞吐量而忽略了背景业务的QoS需求。

同样采用上述实验的网络拓扑与参数设置。令路径上存在两个背景流，背景流1经过第1与第2跳链路而背景流2经过第4至第6跳链路。当其中一个背景流的负载固定为100 kbps时，通过改变另一个背景流的负载来分析整个路径上的可用带宽。图3所示实验结果与预期相符，即可用带宽随着背景负载的增大而下降。此外，背景流2对路径可用带宽的影响大于背景流 1，这是因为背景流 1和背景流2分别经过路径前部和后部节点，由于路径前部节点受到的干扰更大，因此背景流2带来的影响也就更大。图3同时证明了可用带宽估计方法的准确性。

最后我们研究可用带宽与路径长度的关系。为了便于分析，设置路径上无背景负载，此时的估计结果等价于全局QoS保障约束条件下的路径容量。实验结果如图4所示，当路径长度小于6跳时，可用带宽随跳数增加而明显下降；当路径长度超过 6跳后，可用带宽无明显变化。上述现象的原因在于，前一种情况下路径的瓶颈链路受到的干扰随跳数增加而变大，而后一种情况下瓶颈链路受到的干扰不再因跳数增加而增加。

图2 可用带宽估计原则的合理性

6 结束语

本文研究了无线多跳路径的性能分析模型与可用带宽估计问题。详细分析了多跳路径中的干扰现象，并建立了干扰的定量计算模型。在此基础上，基于排队网络理论建立了路径性能分析模型，并利用此分析模型得出路径的时延、丢包率和吞吐量等QoS指标。基于分析模型设计了能提供QoS保障的可用带宽估计方法。本文提出的估计方法的主要优点在于，当估计结果被使用后不会破坏网络中业务流的QoS需求。本文的工作可应用于设计接纳控制方案、速率控制算法与QoS路由协议。

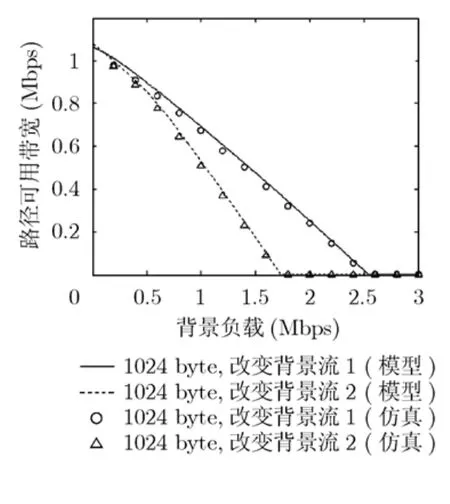
图3 路径可用带宽估计结果

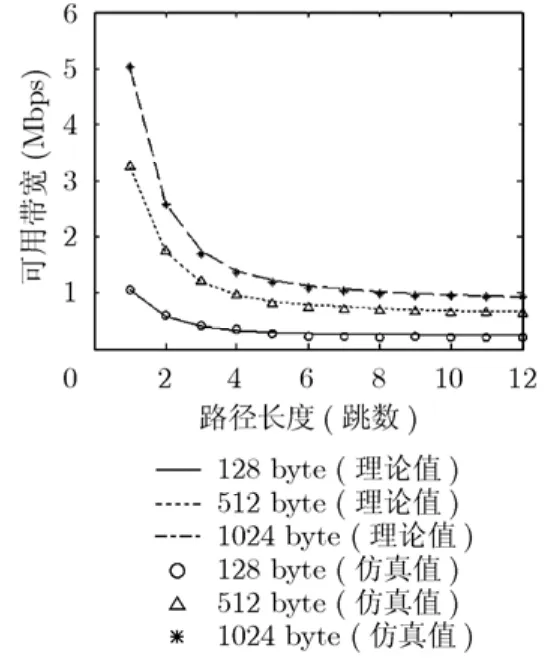
图4 不同路径长度下的路径可用带宽

[1]Strauss J,Katabi D,and Kaashoek F.A measurement study of available bandwidth estimation tools[C].3rd ACM SIGCOMM Conference on Internet Measurement,Miami Beach,FL,USA,2003: 39-44.

[2]Sarr C,Chaudet C,Chelius G,et al..Bandwidth estimation for IEEE 802.11-based Ad hoc networks[J].IEEE Transactions on Mobile Computing,2008,7(10): 1228-1241.

[3]Zhao H,Garcia-Palacios E,Wei J,et al..Accurate available bandwidth estimation in IEEE 802.11-based Ad hoc networks[J].Computer Communications,2009,32(6):1050-1057.

[4]Tursunova S,Inoyatov K,and Kim Y-T.Cognitive estimation of the available bandwidth in home/office network considering hidden/exposed terminals[J].IEEE Transactions on Consumer Electronics,2010,56(1): 97-105.

[5]Zhao H,Wang S,Wei J,et al..Model-based approach for available bandwidth prediction in multi-hop wireless networks[J].Science China:Information Sciences,2011,54(9):1916-1927.

[6]Mao G.The maximum throughput of a wireless multi-hop path[J].Mobile Networks and Applications,2011,16(1):46-57.

[7]Ng P C and Liew S C.Throughput analysis of IEEE802.11 multi-hop Ad hoc networks[J].IEEE/ACM Transactions on Networking,2007,15(2): 309-322.

[8]Zhao H,Wang S,Xi Y,et al..Modeling intra-flow contention problem in IEEE 802.11 wireless multi-hop networks[J].IEEE Communications Letters,2010,14(1): 18-20.

[9]Zhao H,Garcia-Palacios E,Song A,et al..Calculating end-to-end throughput capacity in wireless networks with consideration of the hidden nodes and multi-rate terminals[C].Vehicular Technology Conference (VTC Spring),Budapest,Hungary,2011: 1-5.

[10]Xu K,Gerla M,and Bae S.How effective is the IEEE 802.11 RTS/CTS handshake in Ad hoc networks?[C].Proceedings of IEEE GLOBECOM,Taipei,China,2002: 72-76.

[11]Kumar A,Altman E,Miorandi D,et al..New insights from a fixed-point analysis of single cell IEEE 802.11 WLANs[J].IEEE/ACM Transactions on Networking,2007,15(3):588-601.

[12]Belch G,Greiner S,Meer H D,et al..Queueing Networks and Markov Chains[M].New York: USA,John Wiley ＆ Sons,Inc.,1998: 423-430.

[13]Sakurai T and Vu H L.MAC access delay of IEEE 802.11 DCF[J].IEEE Transactions on Wireless Communications,2007,6(5): 1702-1710.

[14]Wang K,Yang F,Zhang Q,et al..Modeling path capacity in multi-hop IEEE 802.11 networks for QoS services[J].IEEE Transactions on Wireless Communications,2007,6(2):738-749.