第三方物流(TPL)服务供应商的选择——基于二元离散选择模型

刘 洁，李文君

(重庆交通大学管理学院，重庆 400074)

市场竞争日益激烈，企业不再专注于“大而全”的经营模式，而是更加致力于自身核心业务能力，企业将非核心的物流业务外包给第三方物流(TPL)服务提供商是企业提高核心竞争力的一条可行途径［1］。第三方物流市场应运而生，市场中的TPL服务供应商数目众多，发展水平参差不等，选择优质的TPL服务供应商关系到企业长远目标的实现。目前国内外对供应商选择评价的方法主要有层次分析法(AHP)、模糊综合评价法、数据包络分析法(DEA)、灰色关联度分析、人工神经网络分析等［2－3］，这些方法不同程度地应用在各种实践中，对TPL服务供应商的选择提供了基本理论依据，但是每种方法都有其自身的利弊。考虑到备选供应商被选择与否这一事件只存在两种结果，本研究采用二元离散选择模型(binary choice model)来研究TPL服务供应商的选择。首先对备选合作商进行效用评价，建立数据库，然后建立企业选择TPL服务供应商的二元离散选择模型，这种模型为物流外包企业选择合作伙伴提供了辅助性的决策支持。

一、二元离散选择模型概述［4］

(一)模型背景

在经典计量经济学模型中，被解释变量通常被假设为连续的，而在实际分析中会面临许多决策问题，即人们必须在几个备选方案中做出选择，这些备选方案可以用离散的数据表示。例如，某一事件发生与否，分别用1和0表示，对某一建议持反对、中立、支持三种态度，可以分别用0、1、2表示。以这样的决策结果作为被解释变量建立的计量经济学模型，称为离散选择模型DCM(Discrete Choice Model)，被解释变量只能存在两种选择称为二元离散选择模型(binary choice model);被解释变量存在多种选择，称为多元离散选择模型(multiple choice model)。离散选择模型起源于费希纳(Fechner)1860年进行的动物条件二元反射研究，1962年沃纳(Warner)首次将它应用于经济研究领域，用以研究公共交通工具和私人工具的选择问题。

(二)建立模型

对于二元离散选择模型可以建立原始的计量经济学模型:

其中:Yi表示观测值为0和1的决策被解释变量;Xi为解释变量，包括选择对象所具有的属性和选择主体所具有的属性。注意到E(μi)=0，所以

比较式(2)和式(3)，式(2)右端 Xiβ并没有处于［0，1］的区间限制，而 Pi必须处于［0，1］范围内，出现矛盾，所以此原始模型不能作为实际的研究。

为了使二元离散选择研究可行，首先建立随机效用模型。以公共交通工具和私人交通工具的选择问题为例。如果一个个体选择公共交通工具获得的效用为U1i，上标表示选择结果，下标表示第i个个体，该效用是随机变量，于是有

类似地，某一个体选择私人交通工具获得的效用为

式(4)、(5)中效用是不可观测的，被解释变量的观测值仍是0和1，很显然，当＞时人们会选择公共交通工具，对应的观测值为1，相反，≤时人们会选择私人交通工具，对应的观测值为0。

将式(4)、(5)相减，得

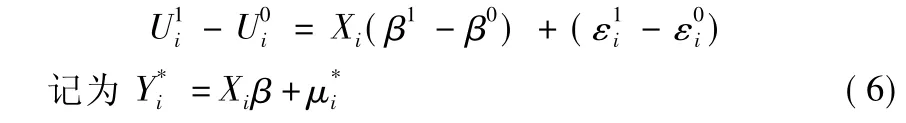
(三)模型总体显著性检验

假设 H0:β1=β2=… =βk=0

备择假设H1:解释变量的系数不全为0。

构造一个似然比(likelihood ratio，LR)统计量:LR=－2(LnL0－LnL)～χ2(k)，其中L0为模型满足0假设(所有解释变量的系数都为0)时的似然函数值，L为模型估计得到的似然函数值。由LR值与χ2分布表值判断模型总体是否显著。

二、TPL服务供应商评价指标的确立

首先分析TPL服务供应商选择的影响因素。从两方面考虑:企业自身方面的因素分析包括企业性质、行业性质、产品特性、物流控制力等，TPL服务供应商方面的因素分析包括TPL供应商服务的水平、价格、服务范围、客户满意度等。

其次建立评价指标体系。TPL服务供应商根据提供的物流种类可分为供应物流、生产物流、销售物流和逆向物流四大类，企业根据自身特点选择合适的TPL服务商，不同企业在设计评价指标时，要遵循全面性、可操控性、可比性和可拓展性的原则，选择有代表性的评价指标组成评价指标体系［5］。这里以单纯性生产制造业为例，生产过程中要求原材料或半成品及时有效运至指定地点，将成品、半成品运至指定客户方，在选择TPL服务供应商时可选取价格、及时率、货损率、服务范围、客户满意度等指标组成物流系统综合评价指标体系。

其中及时率、货损率及客户满意度计算公式:

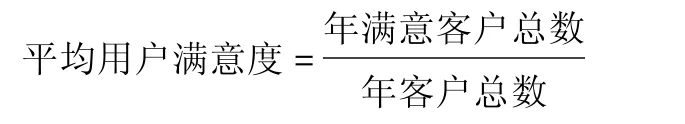
注意，“价格”这个指标虽然是定量指标，但是在评价TPL服务供应商时要规定在同一项业务前提下，在同一个合作项目中各供应商的价格才具有可比性。此外还要注意到“服务范围”这个评价指标无法量化，这给二元离散选择模型的直接建立带来麻烦，所以在应用二元选择模型之前需要对有些变量进行假设，如引入虚拟变量等方法将非量化指标变为可量化的指标。

三、二元离散选择模型的建立及实证分析

1)应用模型前提:在同一个合作项目的条件下在备选供应商中选择最优合作商。

2)模型假设:假设备选供应商中与企业有过合作的视为1，未合作过的视为0。对于“服务范围”这个评价指标，在同一个项目的前提下，物流服务的内容与地点是双方达成共识的，服务范围就只需考虑供应商能否给企业带来增值服务，包括物流业务前期预测、中期控制与后期反馈，供应商的物流服务范围能给企业带来增值服务视为1，否则视为0。假定及时率、货损率、客户满意度其他变量均为连续变量。

3)建立数据库。收集与企业合作过的所有供应商，首先把供应商以合作项目的类别为分类标准进行初步分类。以一汽车零部件生产制造企业为例，企业的物流项目根据零部件的类别将业务进行分类，这样物流供应商就被分为几大类，选取一类进行研究，如选取汽车内饰座椅这一项目，发现与该企业进行洽谈运输汽车内饰座椅的TPL服务供应商共有21家，合作过的TPL服务供应商共有9家，对这21家供应商的资料进行整理，得出表1。

Y:是否与企业合作过，1表示合作过，0表示未合作过。

P:服务价格，每次合作项目平均每千克货物每千米所需费用的报价。

Q:服务质量，为了模型简便，对及时率、货损率和客户满意度综合打分(满分百分制)，采用等权加权平均法计算服务质量综合得分，服务质量=及时率所得分×33．33%+货损率所得分 ×33．33%+客户满意度所得分 ×33．33%。

S:服务范围，物流服务范围能给企业带来增值服务视为1，否则视为0。

4)模型结果。例用计算机Eviews 6．0软件，新建一个work file，录入数据，采用最常用的Probit分布模型对二元离散选择模型进行估计，分析结果如表2。

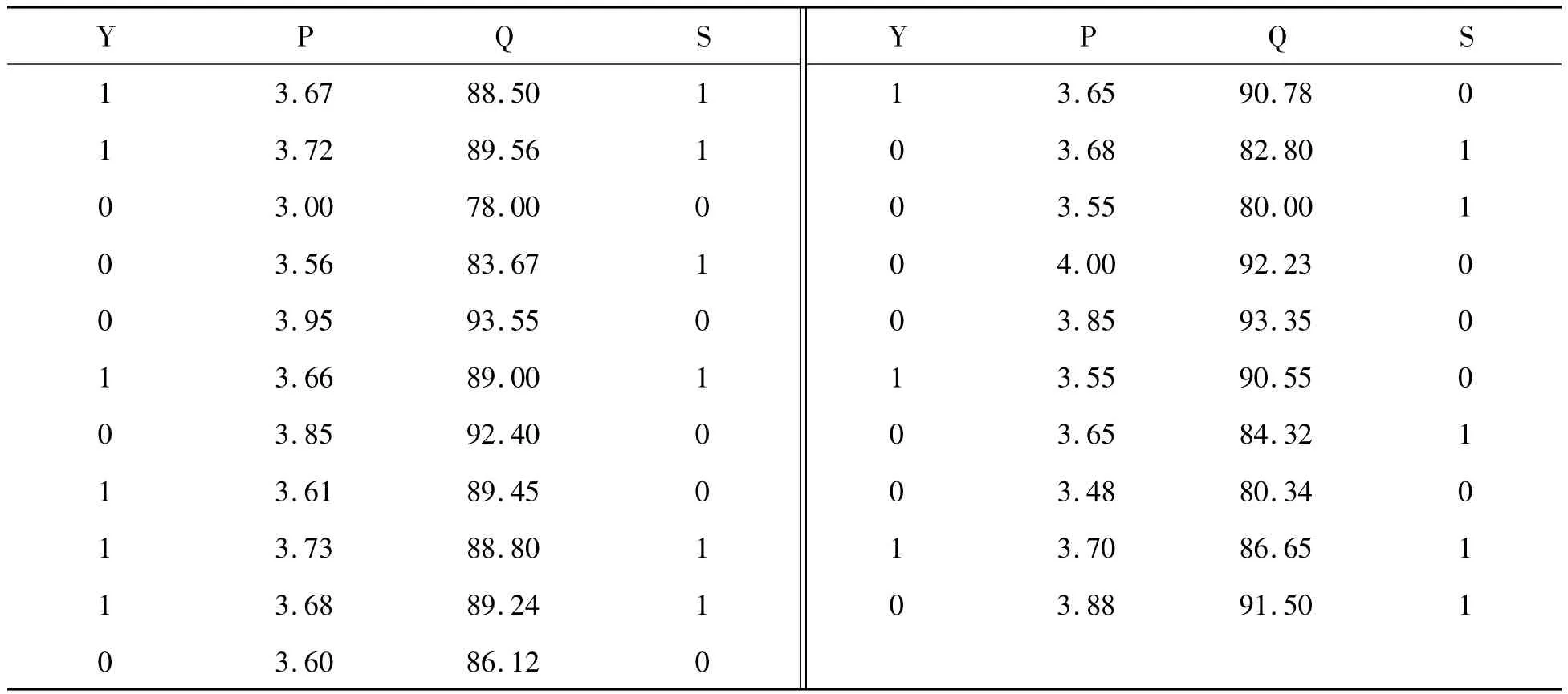
表1 ××企业汽车内饰座椅的合作伙伴数据

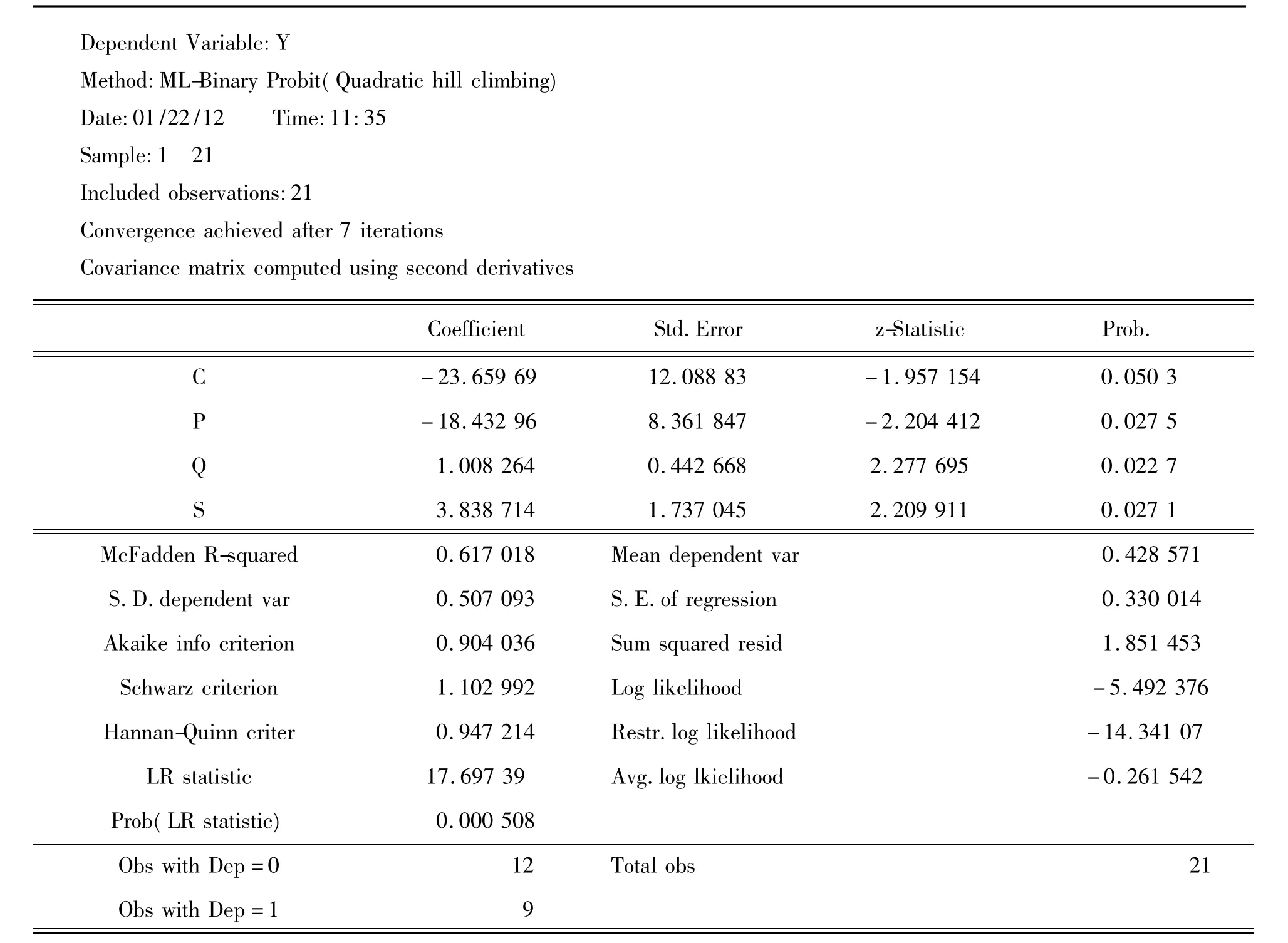
表2 二元离散选择模型估计结果

根据表2可以将估计方程写出，即:

5)模型总体显著性检验。

假设 H0:β1=β2=β3=0

备择假设 H1:解释变量的系数不全为0。

构造一个似然比(likelihood ratio，LR)统计量:LR=－2(LnL0－LnL)～χ2(k)，其中 L0为模型满足0假设(所有解释变量的系数都为0)时的似然函数值，L为模型估计得到的似然函数值。查模型结果表，LnL0的值即表中“Log likelihood”值，为 －5．492 376，LnL的值为表中“Restr．Log likelihood”值，为 －14．341 07，计算得到 LR=17．697 388，由 χ2分布表查得:在95%的置信水平下(3)=7．81，可见，在0．05的显著水平上，该模型拒绝模型总体不显著的0假设。

6)模拟与应用。将上述结果用Eviews工具显示为“Actual Fitted Residual Table”形式，如表3。

观察表中每个被解释变量选择1的概率，发现以朴素概率0．50为临界值时，发生弃真的样本有2个，分别是样本8和样本20，以0．49为临界值，弃真样本只有一个样本20，所以以0．49作为临界值比较合适。

假设企业有一笔汽车内饰物流外包业务洽谈，备选合作商增加了A企业，已知A企业发盘的价格是3．80元/千克千米，根据其资料计算及时率、货损率和客户满意度，然后综合打分计算出服务质量达到90．08分，该企业管理比较完善，可提供物流控制增值服务，那么对应地，P=3．80，Q=90．08，S=1，代入预测方程 Y的预测值 =1－@CNORM( －( －23．659 69 －18．432 96*P+1．008 264*Q+3．838 714*S))，计算括号内的值为 0．958 197，查标准正态分布表，对应于0．958 197的累积正态分布为0．168 5，于是 Y 的预测值为 1 －0．168 5=0．831 5，即对应于A企业，被选择的概率为0．831 5。

四、结束语

企业在选择TPL供应商时，先在分析企业物流特征的基础上构建一套适用于本企业物流的评价指标体系，然后采用直观的招标法进行初步筛选，再对符合条件的备选供应商建立基于最常用Probit分布的二元离散选择模型，得出估计结果，从而为企业决策提供了一种定性与定量相结合的方法，确立选择正确的物流供应商的理论基础。但同时应注意到，这套方法也有其不足之处，如果预测两个TPL供应商的选择概率接近，企业并不总是直接选取概率高者为合作对象，在实践中基于决策者的社会关系等随机原因，有时概率高者并没有被选择;此外，不同的企业必须根据其物流需求建立符合自身企业的评价指标体系，因其工作量繁杂所以目前并无企业完善并采用此方法，该方法仅停留在理论研究上，还需一定的时间推广到实践应用中。

［1］ 王彦庆，朱崇庆．第三方物流服务商承接业务的评价研究［J］．物流技术，2010(20):72．

［2］ 刘振儒，李雪梅．第三方物流服务商绩效评价研究［J］．技术与方法，2010(2):127．

［3］ 杜彦炜．灰关联分析的制造企业第三方物流服务商评价研究［J］．现代制造工程，2010(8):47．

［4］ 李子奈，潘文卿．计量经济学［M］．北京:高等教育出版社，2010(3):237．

［5］ 殷永生，苗海燕．第三方物流服务商评价指标体系的构建分析［J］．当代经济，2008(4):154．