周期载荷下不可压超弹性材料的空穴动生成
2012-09-15任九生沈佳铖袁学刚
任九生,沈佳铖,袁学刚
(1.上海大学 力学系 能源工程力学应用重点实验室,上海 200444;2.大连民族学院 理学院,大连 116600)
因为在材料的破坏过程中起着关键性作用,超弹性材料中空穴生成和预存空穴的突然增长问题得到大量关注[1-3]。Gent等[4]在实验中观察到超弹性材料中的空穴生成现象,Ball[5]基于非线性弹性理论的框架对超弹性材料中的空穴突然生成问题进行了理论分析,将其模拟为一类空穴分岔问题。Horgan等[6-7]将预存空穴的突然增长问题作为对空穴分岔问题的另一种解释。
在有限变形弹性理论框架下,受外边界表面拉伸载荷作用的不可压超弹性球体的平凡解是球体保持其不变形状态。对外加载荷存在一个极限值,当载荷大于这个极限值时,球体中心可能有一个空穴突然生成。现有的关于空穴分岔问题的文献大多分析空穴的静生成问题[1,3,8-9]。但许多物理问题本质上是动态的,在有限变形动力学理论框架下分析惯性力的影响就非常重要[10]。当突加载荷为常值时,动力学系统是自治的,对自治系统的研究方法已较为成熟[11-13]。对受突加常值拉伸载荷作用的不可压超弹性球体也存在一个临界载荷,当突加载荷小于这个临界值时,球体保持不变形状态,但当突加载荷大于这个临界值时,球体中心有空穴突然生成且空穴随时间的演化是周期振动[14-15]。目前对外加载荷为周期载荷的情况还研究得较少,Haslach等[10,16]分析了受周期内压作用的超弹性薄膜的动力学响应,但周期载荷作用下空穴生成的分岔问题尚未得到关注。
本文的目的是在有限变形动力学的框架下分析受外加表面周期载荷作用的超弹性材料球体中的空穴动生成问题。首先由基本假设得到空穴半径和外加周期载荷之间的微分关系,然后通过对一阶微分方程组的Runge-Kutta数值积分得到空穴变形的时程曲线、相图和庞加莱截面图等,通过常用的动力学理论分析了球体的动力学响应和破坏条件。计算结果表明对周期载荷的平均载荷存在一个临界值,当平均载荷小于这个临界值时,球体保持不变形状态;但当平均载荷大于这个临界值时,一个球形空穴可在球体中心突然生成,且空穴随时间的演化为拟周期振动。而且对周期载荷的平均载荷存在另一个临界值,当平均载荷大于这个临界值时,空穴无限增大,球体最终会被破坏。另外讨论了周期载荷的幅值载荷和频率对两个临界值的影响。
1 问题的数学描述
考虑一个半径为B的不可压超弹性球体在外加周期载荷作用下的动力学响应问题。假设球体在外加表面周期载荷p(t)=p1+p2sin(ωt)作用下于t=0开始运动,并假定在时刻t占据(r,θ,φ)的点在未变形前位于点(R,Θ,Φ),则球体的运动模式为:
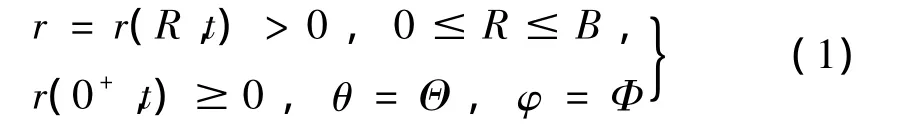
式中,r(R,t)为待定函数。相应的变形梯度张量F为:
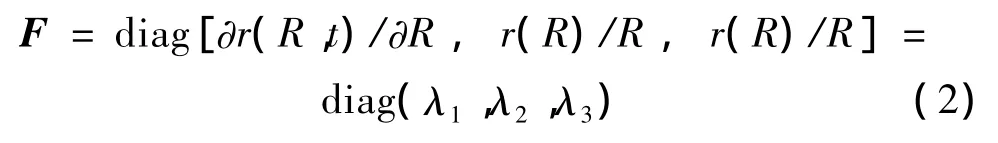
式中,λ1=∂r(R,t)/∂R,λ2=λ3=r(R,t)/R 为变形的主伸长。由材料变形的不可压条件可得:
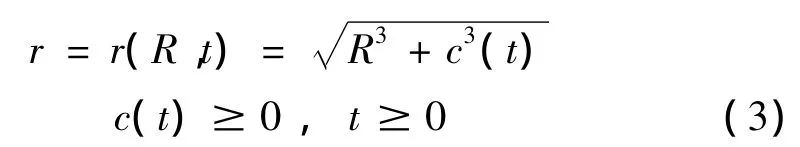
式中,c(t)为待定函数。于是:
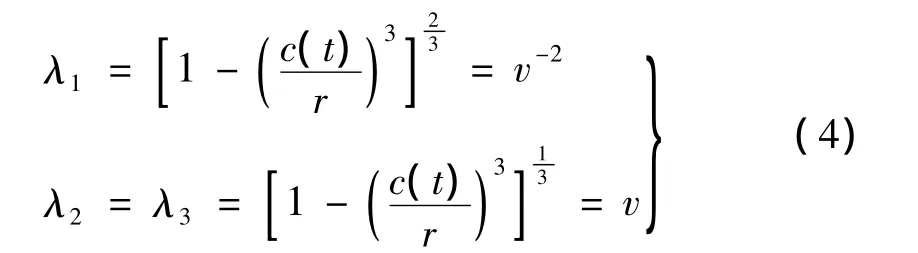
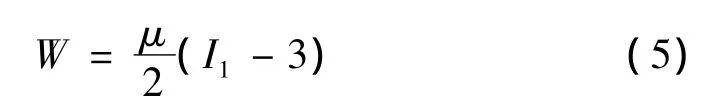
I1=为变形张量的第一不变量,μ为材料的小变形剪切模量。相应的非零Cauchy应力分量为:
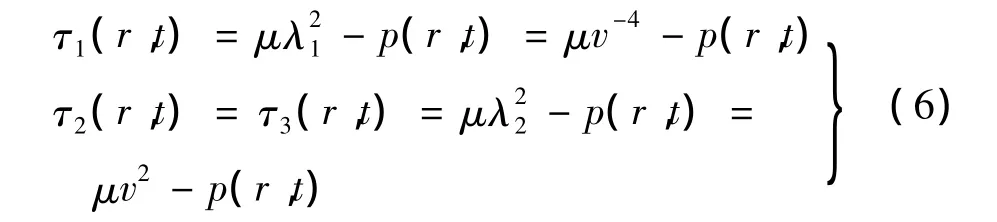
式中:p(r,t)为待定静水压力常数。球体运动方程为:
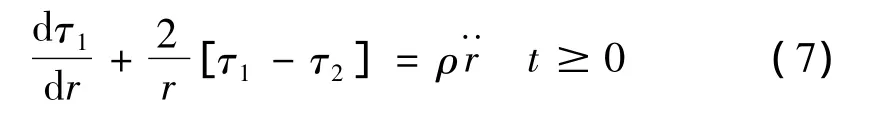
式中:ρ为材料密度。外表面(R=B)边界条件为:
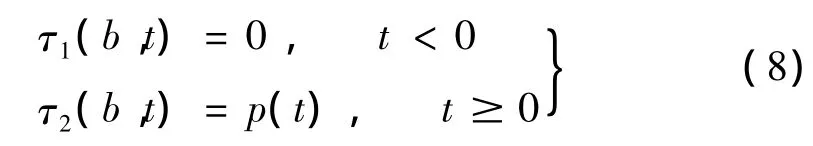
另外,如果有空穴生成,假设空穴表面是自由的:
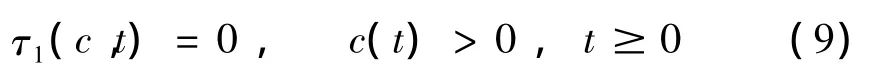
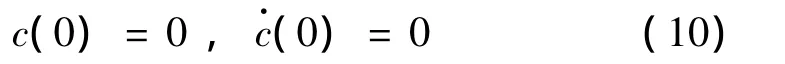
2 求解
对任意的外加载荷p(t),问题总有一个平凡解:

该平凡解相应于球体的未变形状态r(R,t)=R,但此时球体处于一个均匀的应力状态τ1=τ2=τ3=p(t)。为寻求问题的分岔解c(t)>0,将式(3)对t微分可得:
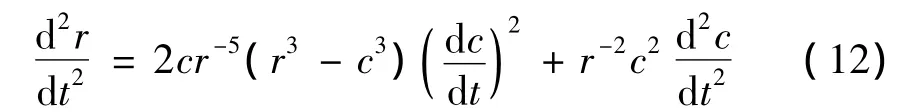
将式(6)和式(12)代入运动方程(7),可得:

将式(13)对r从c到r积分,可得:
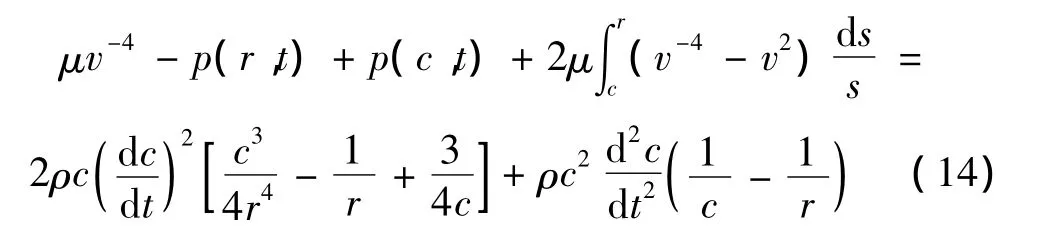
将式(14)代入式(6)有:

将上式代入 式(8)和式(9),有p(c,t)=0和,


则有:

则方程(16)可改写为:

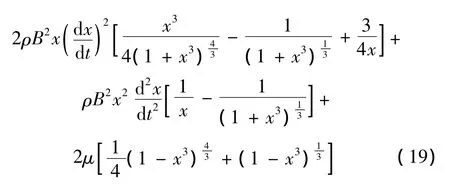

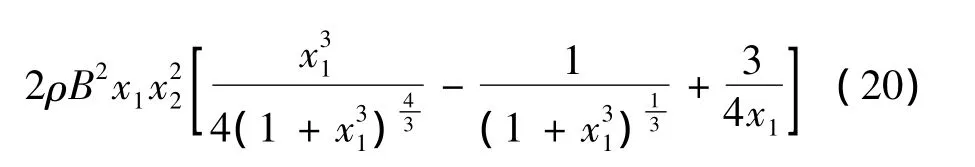
相应的初始条件为:
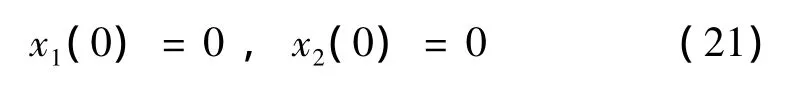
3 结果分析
对形如p(t)=p1+p2sin(3πt)的周期载荷,利用Runge-Kutta方法对式(20)、式(21)进行数值计算可得到空穴变形的时程曲线、功率谱、相图和庞加莱截面图等结果。其中一条时程曲线及其功率谱如图1、图2所示,三个相图如图3~图5所示,三个庞加莱截面图如图6~图8所示。
如通常所示,周期载荷p(t)=p1+p2sin(ωt)的平均载荷为pm=p1+p2。计算过程表明,对给定的幅值载荷p2和载荷频率ω,平均载荷存在两个临界值和。当 pm<时,问题只有一个平凡解x1(0)=0,即此时球体保持未变形状态并无空穴生成现象发生。


表1 平均载荷的临界值(单位:MPa)Tab.1 Critical values for the mean load
4 结论
周期载荷作用下超弹性材料球体中的空穴动生成问题可在有限变形动力学的框架下分析。空穴变形的时程曲线、相图和庞加莱截面图的数值结果和通常的动力学理论分析,表明对周期载荷的平均载荷存在一个临界值,当平均载荷小于这个临界值时,球体保持不变形状态;但当平均载荷大于这个临界值时,空穴可在球体中突然生成,且空穴随时间的演化为拟周期振动。且对平均载荷存在另一个临界值,当平均载荷大于这个临界值时,空穴无限增大且球体最终会被破坏。周期载荷的幅值载荷对第一个临界载荷值有明显的影响,而载荷频率的影响可忽略不计。
[1] Horgan C O,Polignone D A.Cavitation in nonlinearly elastic solids:a review[J].Applied Mechanics Review,1995,48:471-485.
[2] Fu Y B,Ogden R W.Nonlinear Elasticity[M].Cambridge:Cambridge University Press,2001.
[3 ] Gent A N.Elastic instability in rubber[J].Int.J.of Nonlinear Mechanics,2005,40:165-175.
[4] Gent A N,Lindley P B.Internal rupture of bonded rubber cylinders in tension[J].Proc.R.Soc.London,1958,249:195-205.
[5] Ball J M.Discontinuous equilibrium solutions and cavitation in nonlinear elasticity[J].Phil.Trans.R.Soc.London,1982,A306:557-610.
[6] Horgan C O,Abeyaratne R.A bifurcation problem for a compressible nonlinearly elastic medium:growth of a microvoid[J].J of Elasticity,1986,16:189-200.
[7] Sivaloganathan J.Uniqueness of regular and singular equilibria for spherically symmetric problems of nonlinear elasticity[J].Arch.Rational Mech.Anal,1996,96:96-136.
[8] Wang M S C,Horgan C O.Void nucleation and growth for a class ofincompressible nonlinearly elastic materials:an example[J].Int.J.of Solids and Structures,1989.25:1239-1254.
[9] Merodio J,Saccomandi G.Remarks on cavity formation in fiber-reinforced incompressible nonlinearly elastic solids[J].Europrean J.of Mechanics A/Solids,2006,25:778-792.
[10] Haslach A D,Humphrey J D.Dynamics of biological soft tissue and rubber:internally pressurized spherical membranes surrounded by a fluid[J].Int.J.of Nonlinear Mechanics,2004,39:399-420.
[11] Guo Z H,Solecki R.Free and forced finite amplitude oscillations of an elastic thick-walled hollow sphere made of incompressible material[J].Arch.Mech.Stos ,1963,15:427-433.
[12] 任九生,程昌钧.可压超弹性球壳的有限振动[J].振动与冲击,2003,22(4):1-4.
[13] 任九生.热超弹性圆柱壳的振动与破坏[J].振动与冲击,2008,27(12):36-39.
[14] Wang M S C, Horgan C O. Cavitation in nonlinear elastodynamic for neo-Hookean materials[J].Int.J.of Engng.Sci.,1989,27:967-973.
[15] 任九生,程昌钧.超弹性材料中空穴的动态生成[J].固体力学学报,2004,25:42-46.
[16] Shah A D,Humphrey J D.Finite strain elastodynamics of intracranial saccular aneurysms [J].J.of Biomech,1999,32:593-599.
