基于时频的频带熵方法在滚动轴承故障识别中的应用
2012-09-15王小玲从飞云
王小玲,陈 进,从飞云
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
滚动轴承是应用最为广泛的机械零件之一,同时也是机械设备中最容易损坏的元件之一。据统计,在使用滚动轴承的旋转机械中,大约有30%的机械故障都是由于轴承引起的。因此对轴承的故障识别和诊断一直机械故障诊断的重点和热点。
研究表明,轴承信号具有非平稳性,传统的信号分析方法常常受到限制,因为不能同时得到信号在时域和频域的信息。时频分析是一种比较有力的非平稳信号分析工具。它能够建立信号能量在时间和频率上的分布,在此基础上进行分析和处理,可以更有效提取信号中包含的特征信息[1]。单纯的时频分析结果并不便于直接进行故障的监测和诊断,其后续处理是多种多样的。近年有许多研究在时频分析的基础上,进行了故障监测指标的提炼,以更直观地进行故障诊断。Dwyer[2]将时域的峭度指标引入到频谱分析中,提出了谱峭度的概念,Antoni[3]对此进行了深入的研究,提出了基于短时傅里叶变换(STFT)的谱峭度法,并将其用于实际机械故障的诊断。林京等[4]将信息熵与短时傅里叶变换相结合,提出了信号时频熵的概念,并将其用于齿轮故障诊断;申弢等[5]将信息熵与小波分析相结合,提出了小波能谱熵和小波空间状态特征熵的概念,并将其用于转子系统故障诊断。
相比于峭度等传统故障监测指标,信息熵在故障检测领域是一个较新的概念,是对系统复杂性程度的描述。当机器出现故障时,其振动状态的复杂性将会变化,因此信息熵从一个新的角度反映系统当前的工作状况,可以作为监测机器状态变化的一个指标或故障特征[5]。对于非平稳信号,将信息熵和时频分析相结合,可以更有效地提取信息。本文在此思想上提出频带熵方法,并通过实验以及与其他指标的对比,表明其能准确识别轴承故障,具有实用效果。熵的概念。
设由一个离散随机变量{X}={x1,x2,…,xN}所给定的信源,其出现的概率 Pi=P(xi)(i=1,2,…,N),且,则信源X的信息熵表示为:
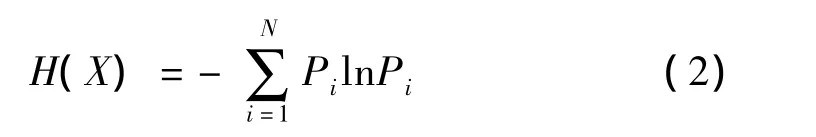
其中:定义ln0=0。
信息熵是从平均意义上表征信源总体信息测度的一个量,同时又是对信源输出信息的不确定性和事件发生的随机性的度量。当信源中每个变量以等概率出现时,即时,信息熵取得最大值lnN,此时信息量最大。而当信源中只是某一变量以概率1出现时,即Pn=1,Pi=0(i≠n)时,信息熵取最小值0,此时该信源包含的信息量最小。概括而言,当信源中各个变量的概率分布越均匀时,信息熵越大,信源包含的信息量越大,反之,当信源中各个变量的概率分布越不均匀时,信息熵的值越小,信源包含的信息量也越小。
随着信息熵在各个领域的应用,逐渐演化出各种形式的熵,如样本熵、近似熵、谱熵等,其中谱熵在故障诊断中使用较多,包括奇异谱熵、幅值谱熵、小波能谱熵等。在众多形式的熵中,以幅值谱熵的意义最为简单明了,且在计算速度上具有绝对的优势。
幅值谱分析是最常用的频域分析方法,将其与信息熵结合,即为幅值谱熵。归一化的幅值谱熵计算如下:
颈椎轴性症状(axial symptoms,AS)评价采用四分法:优,术后无颈部不适症状;良,症状出现在劳累或受凉时,症状较轻,对生活工作影响不大,休息或卧位可缓解,无需服用止痛药物;可,症状出现较为频繁,但每年不超过约3个月,颈部可有压痛痉挛,服用止痛药物缓解;差,症状出现很频繁,超过3个月,颈部疼痛僵硬、麻木症状严重,止痛药物效果不佳。其中“优”和“良”定义为无轴性症状,“可”和“差”定义为有轴性症状【4】。

1 信号的频带熵
1.1 时频分析原理
传统的傅里叶变换在表征非平稳信号时存在一定的局限性,难以揭示非平稳信号频率分量随时间的变化情况。时频分析方法用时间和频率的联合函数来表示非平稳信号,克服了传统傅里叶变换的这一缺陷,是非平稳信号分析更为准确有效的一种方法。常用的时频分析方法有:短时傅里叶变换(STFT)、魏格纳-维尔(Wigner-Ville)分布和小波变换(WT)等。
本文采用STFT的时频分析方法。为了在时域上局部化,在信号进行傅里叶变换前乘上一个时间有限的窗函数,并假定非平稳信号在窗函数的短时间间隔内是平稳的。通过窗在时间轴上的移动从而是信号逐段进入被分析状态,这样就可以得到信号的一组“局部”频谱。从不同时刻“局部”频谱的差异上,便可得到信号的时变特性,实现了在时间域和频率域上都具有较好局部性的分析方法,这种方法就称为短时傅里叶变换。
设h(t-τ)是中心位于τ宽度有限的时间窗函数,与信号x(t)做乘积运算,实现在τ附近的开窗和平移,再做傅里叶变换,即:
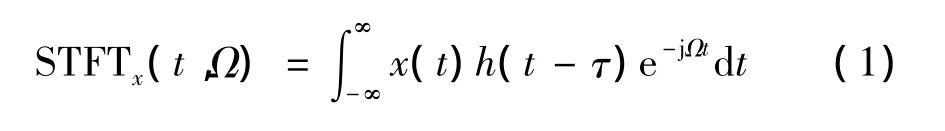
式中:h(τ)的作用是保持在时域为有限支撑,其宽度越小,则时域分辨率越好;在频域,由于ejΩτ为δ函数,也可保持较好的频域分辨率[1]。短时傅里叶变换大致反映了x(t)在时刻τ频率Ω处的信号成分的相对含量,是时频分析的基本方法[1,6]。
1.2 幅值谱熵
“熵(Entropy)”的概念最早出现在热力学和统计物理学中,后来泛化到信息论域。Shannon[7]运用概率论和数理统计学方法,将熵的概念推广到信息理论,把信息定义为“熵的减少”,即“系统或事物不确定性的减少”,首次提出了对信息进行定量描述的方法,即信息
其中:X(i)为序列{xi}(i=1,2,…,N)的幅值谱,Hs为幅值谱熵。
幅值谱熵度量了信号的频率分布均匀程度,体现了信号能量分布的频域复杂度。当信号能量集中在少数的几个频率成分时,幅值谱熵取值小,尤其是信号为单一成分时,即信号能量集中在某一个单一频率下时,幅值谱熵取得最小值0;而当信号频率成分越是复杂,即信号能量分布在众多频率下时,幅值谱熵取值越大,尤其当信号在整个频带内均匀分布时,幅值谱熵取得最大值1。幅值谱熵的大小只取决于信号的频率分布,而与信号的强弱无关。
1.3 基于幅值谱的频带熵方法
幅值谱熵可以表征在一段时间内频率结构的复杂度,但却不能揭示在这段时间内频率分量随时间的变化情况。为了揭示频率分量随时间变化的复杂度,结合时频分析,提出一种新的分析方法——基于幅值谱的频带熵分析方法。
对原信号{xi}(i=0,1,…,N-1)作时频变换,得到信号的时频分布矩阵(行为时间分布,列为频率分布):
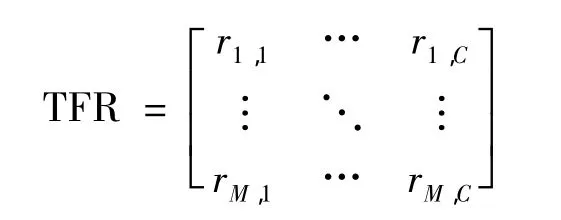
其中:M为频率点数;C=N/L,L为窗函数沿时间轴移动的步长。
对频率 fj处的时间分布{rn,i}(i=1,2,…C)计算幅值谱熵:

频带熵表征的是某一频率成分随时间变化的复杂性。如果某一频率成分一直比较稳定或者规律的存在于信号中,则该频率线上的谱熵值会比较小;若频率分量在一段时间内有复杂的波动,那么它的谱熵值较大。取一段时间内全频带的最小谱熵作为该段信号的频带熵,表征该时间段内频率变化的复杂度。
频带熵与文献[4]中的时频熵以及文献[5]中的小波熵的区别在于:时频熵是按时频块划分能量,小波熵按尺度划分能量,两者在整个时频分布上得到一个熵值,是一种比较宏观的划分;而频带熵是对每一个频率都进行谱熵计算,在全频域得到一条幅值谱熵曲线,是一种相对微观的划分,更充分的利用了时频联合分析所提供的信息,能更好表征信号的动态变化。
在故障监测中,常会因为某些偶然因素如传感器异常、电压波动等,而使采集的信号产生冲击干扰,即数据奇异点。一般希望监测指标既能够准确地指示轴承故障,又具有良好的抗干扰性。大多数指标能够示出轴承故障,但抗干扰性却不够理想,例如工程中常用的峭度、裕度、脉冲、峰值等指标,虽然对故障的反映比较明显,但往往也会因为这些奇异点产生突变,引起误判断。谱峭度指标基于时频分析的思想,计算每一根谱线上的峭度值,通过细查全频带来检出故障所在[3],与频带熵方法有一定相似之处,但它对暂态冲击成分非常敏感,因此不能排除奇异点的影响,其识别效果与抗干扰性也较差。
频带熵的优点在于既能明确的指示轴承状态,又有很好的抗干扰性。滚动轴承在正常状态下的时域信号近似为高斯分布,其中的奇异点在经过频带熵各个步骤处理后,频谱呈白噪声特征,对频率分布的复杂性没有影响,所以不会影响幅值谱熵。可见,频带熵的计算原理决定了它能够自动消除数据奇异点的影响,具有良好的抗干扰性。
2 实验验证
2.1 故障识别验证实验
为验证本文所提出的时频熵方法在实际轴承故障诊断中的应用价值,进行实验验证。图1为实验设备的安装构成图,此实验在滚动轴承测试实验台ZST-1上进行,数据采集卡采用 NI6023e,采集软件使用labview编写,采样频率为 25.6 kHz。
对正常轴承和故障轴承各连续采集16组信号,分别计算其谱峭度与频带熵,结果如图2、图3所示。
图2所示谱峭度曲线,可以看到其波动较大,在正常状态和故障状态存在较多的交叠区域,识别效果不甚理想。


图3 正常信号与故障信号的频带熵对比Fig.3 Spectrum band entropy of normal and fault signals
图3为频带熵曲线,频带熵能够非常清晰地区分正常信号与故障信号,辨别效果优于谱峭度,辨别区间比较明显。图中所示正常信号的频带熵比故障信号的要大,因为滚动轴承在正常状态下的振动时域信号近似为高斯分布,此时信号中非噪声成分主要源于保持架转频和轴频,以及保持架对轴的旋转产生的微弱调制,信号能量在频域分布比较均匀,频带熵取值相对较大。而轴承一旦产生故障,信号能量就会逐渐集中到故障特征频率(带)上,信噪水平增加,信号的频率分布变得越来越规则,频带熵的取值就会变小。通过对其他多组数据的分析,表明频带熵具有稳定的辨识效果。为了更好的应用机器自动识别,减少人工参与,可在频带熵基础上引入支持向量机分类方法或者基于概率统计的分类法[8-11]。在同时具有正常和故障的先验数据时,以两种状态下的频带熵作为支持向量,对支持向量机进行训练,之后可实现对新数据的分类,进行状态识别。在只有正常轴承信号的情况下,则可以采用基于概率统计的分类法。建立正常状态下的频带熵概率分布规律,以一定的准则确定判别阈值,如正态分布下的“3σ”准则,通过阈值来判定轴承正常与否。
2.2 鲁棒性论证实验
为了验证频带熵方法在故障识别中的鲁棒性,将其应用于实际的轴承加速疲劳寿命实验信号。实验在联合国援助杭州轴承试验研究中心国家检测实验室(CNAS No.L0309 ISO/IEC 17025国际互认)进行,利用其国际标准化的轴承疲劳试验装置,进行轴承的全寿命周期加速试验,采用的轴承型号是6307,轴承从正常开始,通过数据采集装置采集其振动信号,直至轴承失效为止。图4所示为本次试验的现场设备装置全图。振动信号通过加速度传感器首先进过NI的scxi信号调理模块进行抗混叠滤波,然后接入NI的PCI数据采集卡6023e进行数据采集,相关的采集采集软件也使用NI的Labview平台进行编写,系统采样频率设置为25.6 kHz,每隔一分钟保存一组振动信号数据,每组数据长度为20 480。设备从开始到出现报警停机,共采集1 062组数据。

图4 实验设备安装图Fig.4 Installing drawing of experiment
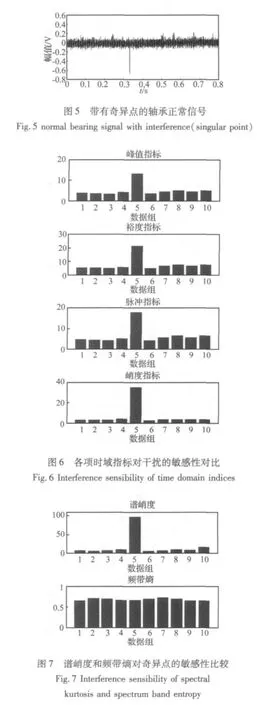
在轴承正常阶段取连续10组信号进行分析。其中第5组含有干扰(奇异点),如图5。发现峭度、裕度、峰值、脉冲指标均在第5组显示出突变,如图6所示,表明上述各项时域指标不能排除干扰,鲁棒性较差。
图7显示了两个时频域指标对干扰的反应,谱峭度对奇异点的敏感性非常突出,而频带熵指标没有明显的异常,说明频带熵对于奇异点不敏感,可以有效排除干扰,具有良好的鲁棒性。频带熵这一特性有利于减少系统监测中的误判断和误报警,具有实用价值。
3 结论
基于时频分析和信息熵理论,提出了频带熵方法,用于滚动轴承故障监测。频带熵相比于小波能谱熵等基于时频分析的谱熵指标,能够更全面的考量非平稳信号中所包含的信息。与多个传统的时域指标以及基于时频的谱峭度指标相比,频带熵对偶然因素引起的数据奇异不敏感,具有更好的抗干扰性。通过对实测数据的应用,表明频带熵能够自动排除干扰的影响,准确清晰地识别滚动轴承的状态。
[1] 张贤达,保 铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998.
[2] Dwyer R F.Detection of non-Gaussian signals by frequency domain kurtosis estimation[C].International Conference On Acoustics,Speech,and Signal Processing,Boston,1983,607-610.
[3] AntoniJ. The spectral kurtosis:a useful tool for characterizing non-stationary signals [J]. Mechanical Systems and Signal Processing,2006,20:282-307.
[4] 林 京,屈梁生.信号时频熵及其在齿轮裂纹识别中的应用[J].机械传动,1998,32(2):37-39.
[5] 申 弢,黄树红,韩守木,等.旋转机械振动信号的信息熵特征[J].机械工程学报,2001,37(6):94-98.
[6] 向 玲,唐贵基,胡爱军.旋转机械非平稳振动信号的时频分析比较[J].振动与冲击,2010,29(2):42-45.
[7] Shannon C E.A mathematical theory of communications[J].Bell System Technical Journal,1948,27:379-423.
[8] 袁胜发,褚福磊.支持向量机及其在机械故障诊断中的应用[J].振动与冲击,2007,26(11):29-35.
[9] 张 超,陈建军,郭 迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击,2010,29(10):216-220.
[10] 桑林琼,邱明国,王 莉,等.基于统计阈值的脑肿瘤MRI图像的分割方法[J].生物医学工程研究,2010,29(4):237-239.
[11] 官燕燕,刘 昕.基于统计阈值法的印品缺陷检测[J].西安理工大学学报,2007,23(4):410-413.
