基于LMD的谱峭度方法在齿轮故障诊断中的应用
2012-09-15程军圣
程军圣,杨 怡,杨 宇
(湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082)
常见的齿轮故障振动信号往往表现为调制形式,获取幅值或频率调制信息是提取故障特征的关键。包络解调技术是齿轮故障诊断中的常用方法,但其解调过程中的滤波参数取决于操作者的经验或历史数据[1-2],这对于诊断结果的准确性会产生一定的影响。采用EMD(Empirical Mode Decomposition,简称 EMD)等自适应信号分解方法可以自动地将齿轮故障振动信号分解为若干个分量,然后选择合适的分量进行解调分析[3],但是如何选择合适的分量仍然需要进行研究。当齿轮发生局部故障时会引起齿轮振动信号中产生瞬态冲击脉冲,而该脉冲频率通常即为齿轮信号的故障特征频率[4]。谱峭度的概念由 Dwyer[5]提出,其实质是在时频分析后反映原始信号在每个谱段上的峭度大小,它能够有效地反映非平稳性的存在,检测含噪信号中的瞬态成分[6],对故障脉冲信号非常敏感,并明确地指出瞬态成分所在的频带,为滤波参数的选取提供依据。
最早的谱峭度是基于短时傅里叶变换(STFT)提出的,具有一定时间长度的窗口在时间轴上按一定的步长移动,计算移动窗口内的频谱则得到不同时段信号的频谱,然后对不同的频带计算其峭度即得到所谓的谱峭度。Antoni[7-8]将谱峭度方法规范化,并提出了谱峭度的快速算法-峭度图,并将该方法运用到故障诊断中取得了较好的效果,但其主要还是基于STFT和有限冲击响应(FIR)滤波器[9],STFT受固定窗口长度的限制不能同时兼顾时间分辨率和频率分辨率,而FIR滤波器也不可能与每一种含特征波形的故障信号实现最佳匹配,因此峭度图的应用有一定的局限性。国内的石林锁等人提出了一种基于连续小波变换的谱峭度改进包络分析方法,连续小波变换克服了STFT时频窗口不能改变的缺点,自适应性更高,但其仍存在所得的信号分解结果只与分析频率有关而与信号的本身频率无关等缺点,直接影响到谱峭度方法对故障特征频段的提取效果。针对这些不足,本文提出了基于LMD时频分析的谱峭度故障诊断方法。LMD是一种新的时频分析方法[10],较之STFT、小波变换等方法具有更强的自适应性,它能将一个复杂的多分量信号从高频至低频自适应地分解为有限个有物理意义的乘积函数(Product Function,PF)分量之和,较之现在常用的EMD方法,它的迭代次数更少,且能更好的抑制端点效应,更加完整的保留信号信息[11],因此,将 LMD方法与Hilbert变换相结合能够得到更加准确的信号时频分布,再在时频分布的基础上将信号按照不同的尺度分成若干频段,计算每一频段的谱峭度,根据谱峭度最大原则选取出相关频段信号做包络分析,避免了滤波参数选择对人的经验和历史数据的依赖性,有效地检测到瞬态信号。实验结果表明,基于LMD时频分析的谱峭度方法能够成功地提取齿轮故障特征达到齿轮故障诊断的目的。
1 基于LMD时频分析的谱峭度齿轮故障诊断方法
LMD方法的实质就是将非平稳调制信号分解为若干由包络信号和纯调频信号乘积而得的PF(Product Function)分量,根据文献[11],对于任意原始信号x(t),其经过LMD分解后每个PF分量均可写成如下形式:

其中:包络信号ai(t)为PF分量的瞬时幅值,而PF分量的瞬时频率可以通过纯调频信号si(t)求得:

由式(1)、式(2)知,最后原始信号由下式表示:
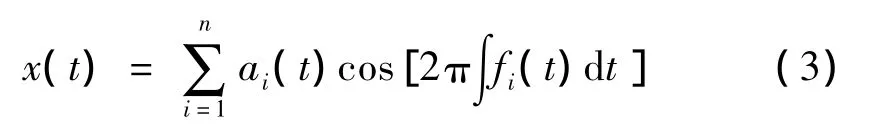
其中:ai(t)、fi(t)分别为PF分量的瞬时幅值与瞬时频率,n为PF分量的个数,这里忽略了余量。在式(3)中由于每个PF分量的瞬时幅值与瞬时频率都是随时间变化的,因此借鉴 Hilbert谱[10-11]的思想,定义式(3)右边部分为基于LMD的时频分布,记作:

式中:S(f,t)反映了信号幅值随时间和频率的变化关系。
得到信号的LMD时频分布后,再按照不同的尺度l将时频信号分成一系列的若干频段mnl,其中n为每一尺度所对应的信号频段数,若信号的频率范围为[0,f],则:
当l=1时:

当l=2时:

具体每一尺度所对应的频段数可以根据实际情况确定,只要下一尺度的频段数多于其上一尺度即可,当信号的采样频率越高时,需要通过越多的尺度来进行分解,这样才足以细化频段从而寻找最佳滤波频段。通过时频分析得到一系列的频段后,再根据式(7)计算每一频段的谱峭度:
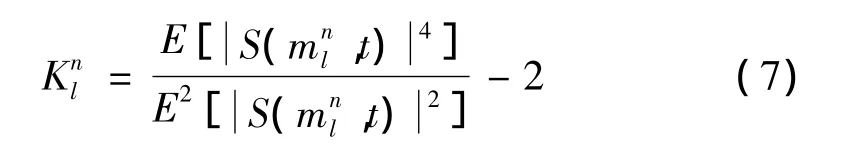
最后,依据谱峭度最大原则选取最佳滤波频段,对该频段信号进行包络分析后即可提取齿轮故障特征进行故障诊断。
2 仿真信号分析
为了验证该方法的可行性,考察如式(8)所示的仿真信号x(t):

该信号由两个调制分量组成,添加均值为0,方差为1的白噪声序列。图1(a)为信号的时域图,图1(b)为信号经过LMD分解所得的前三个PF分量,由分量不能直接十分明显的看出调制信息。图2是信号基于LMD时频分析的峭度图,从图中可知,在第9层第7频段出现峭度最大值,在第11层第3频段出现峭度次大值,分别以该两频段为第一滤波频段和第二滤波频段对信号进行FIR滤波后得到如图3所示的时域波形,其中图3(a)为第一频段滤波时域波形,图3(b)为第二频段滤波时域波形,图4为其对应的包络谱图,在图3(a)、(b)中已经可以很明显的看出调制频率,而在图4则是通过谱图直观地把调制频率表示出来,可以明显观察到两分量的幅值调制特征频率6 Hz和20 Hz,证明基于LMD时频分析的谱峭度方法有效地提取出了仿真信号的调制信息。

3 基于LMD时频分析的谱峭度方法在齿轮故障诊断中的应用
当齿轮出现断齿、裂纹、磨损等故障时,齿轮啮合振动信号的幅值和相位均会发生变化,产生幅值和相位调制,图5为一断齿故障齿轮的时域波形,齿轮信号采集实用装置及测量方法见文献[12],其采样频率为1 024 Hz,转频为7 Hz,该齿轮故障信号经LMD时频分析后的时频图如图6所示,在图上不能看出任何故障信息,图7是基于LMD时频分析所得到的峭度图,从该图中可以看出在第11层第14频段上谱峭度取得最大值,说明此频段包含了齿轮振动故障信息,以此为滤波频段对该信号进行滤波包络后得到如图8所示的齿轮断齿故障信号包络谱,在图中可以看到在7Hz处具有明显谱线,该频率刚好与齿轮的工作转频相吻合,证明该齿轮确实存在局部故障。基于LMD时频分析的谱峭度法成功地提取出齿轮故障特征。
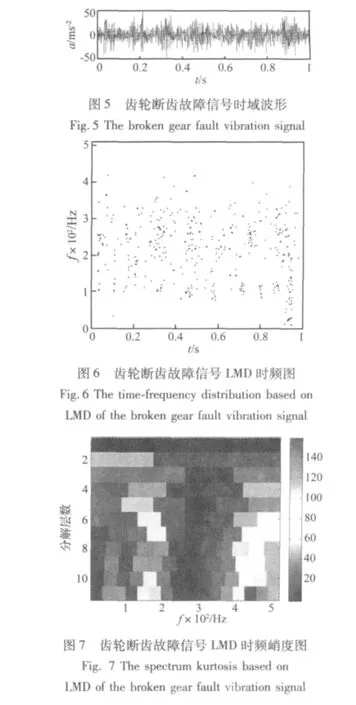

图8 齿轮断齿故障信号滤波后包络谱图Fig.8 The envelope spectrum of filtered broken gear fault vibration signal
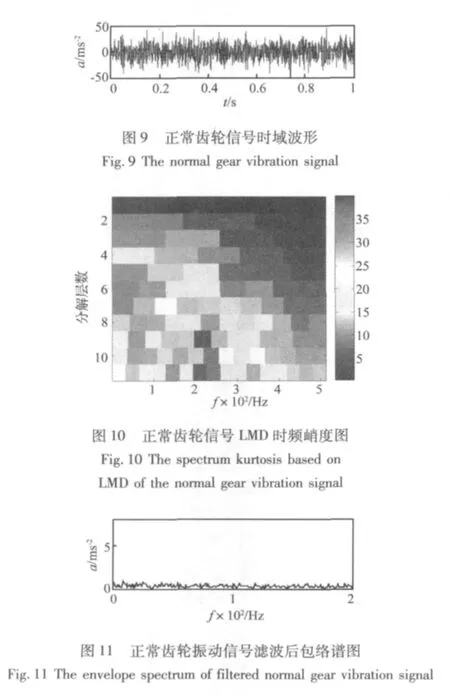
当将基于LMD时频分析的谱峭度方法用于正常齿轮时,齿轮的峭度图各频段峭度值明显小于断齿故障齿轮,且其经过滤波包络后谱图上也不会发现明显故障特征谱线。图9是一正常齿轮的时域波形,采样频率仍为1 024 Hz,转频仍是7 Hz,图10是其经过LMD时频分析后得到的峭度图,由图可知,在第9层第6频段出现了相对较大谱峭度,且整个峭度图中的最大峭度值在40左右,对比图7的最大谱峭度值150其降低了很多,同时经过最优频段滤波包络后得到的谱图图11中也没有发现明显谱线。
为了证明LMD时频分析方法与谱峭度方法相结合的优越性,本文用基于EMD时频分析的谱峭度方法对同一断齿故障齿轮信号做了对比分析。图12为断齿故障信号的EMD时频分解,图13为经过EMD时频分析后得到的峭度图此时在第10层的第12频段取得了最大峭度值,以此为滤波频段对信号进行滤波包络后得到如图14所示谱图,图中也可以看见在7Hz处存在明显谱线,但不如图8突出,证明了基于LMD时频分析的谱峭度方法在齿轮故障诊断中的优越性。

4 结论
本文介绍了基于LMD时频分析的谱峭度方法,并将其引用到齿轮故障诊断中。谱峭度方法是基于信号时频分析提出的,其实质就是计算信号细小频段甚至每条谱线的峭度值,谱峭度对瞬态信号及其敏感,因此能够有效地检测到信号的不平稳性,提取出齿轮信号的故障特征频段。LMD时频分析方法相对于其他的常见时频方法(如STFT,小波变换等)具有更好的自适应性,因此能够更加真实的显现出信号的时频分布。基于LMD时频分析的谱峭度方法能够通过峭度最大原则检测出包含故障特征信息的频段,对其进行包络分析后提取出故障特征频率。结果表明,基于LMD时频分析的谱峭度方法能够有效地运用于齿轮故障诊断中。
[1] Nikolaou N G,Antoniadis I A.Demodulation of vibration signals generated by defects in rolling element bearings using complex shifted morlet wavelets[J].Mechanical Systems and Signal Processing,2002,16(4):677-694.
[2] Yiakopoulos C T, Antoniadis I A. Waveletbased demodulation of vibration signals generated by defects in rolling element bearings[J].Shock and Vibration,2002,9(6):293-306.
[3] Parey A,Guillet M E,Tandon N.Dynamic modeling of spur gear pair and application of empirical mode decompositionbased statistical analysis for early detection of localized tooth defect[J].Journal of Sound and Vibration,2006,294(3):547-561.
[4] Cheng J S,Yu D J,Yang Y.The application of energy operator demodulation approach based on EMD in machinery faultdiagnosis[J]. MechanicalSystems and Signal Processing,2007,21(2):668-677.
[5] Dwyer R F.Detection of non-gaussian signals by frequency domain kurtosis estimation[C].Int.Conf.Accoustic,Speech,and Signal Processing,Boston,1983:607-610.
[6] 蔡艳平,李艾华,石林锁,等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击,2011,30(2):167-172.CAI Yan-ping,LI Ai-hua,SHI Lin-suo,et al.Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J].Vibration and Shock,2011,30(2):167-172.
[7] AntoniJ. The spectral kurtosis:a useful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing,2006,20(2):282-307.
[8] Antoni J.Fast computation of the kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing,2007,21(1):108-124.
[9] 王晓冬,何正嘉,訾艳阳.滚动轴承故障诊断的多小波谱峭度方法[J].西安交通大学学报,2010,44(3):77-81.WANG Xiao-dong,HE Zheng-jia, ZIYan-yang. Spectral kurtosis of multiwavelet for fault diagnosis of rolling bearing[J].Journal of Xi’an Jiaotong University,2010,44(3):77-81.
[10] Smith J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface,2005,2(5):443-454.
[11] 程军圣,张 亢,杨 宇,等.局部均值分解方法与经验模式分解的对比研究[J].振动与冲击,2009,28(5):13-16.CHENG Jun-sheng,ZHANG Kang,YANG Yu,et al.A comparison between the local mean decomposition and the empirical mode decomposition method[J].Vibration and Shock,2009,28(5):13-16.
[12] Yang Y,He Y,Cheng J S,et al.A gear fault diagnosis using Hilbert spectrum based on MODWPT and a comparison with EMD approach[J].Measurement,2009,42(4):542-551.
