拟合核电厂多维设计反应谱及相关峰值的地震动调整方法
2012-09-15谢异同施卫星
盛 涛,谢异同,袁 俊,施卫星
(1.同济大学 结构工程与防灾研究所,上海 200092;2.西安建筑科技大学 土木工程学院,西安 710055;3.西北电力设计院,西安 710075)
核电厂的抗震性能一直是核电站结构设计的主要问题之一。我国核电厂抗震设计规范[1]以频率控制点及伪速度反应谱的形式给出了基岩及硬土场地条件下的多维标准反应谱,要求输入不少于三组分别包含水平向及竖向分量的加速度时程用于其动力反应分析,并指出了生成人工波的两种方法,即三角级数叠加法和调整实际地震加速度记录。
在三角级数叠加法研究中,胡聿贤等[2-5]均给出了适合各自研究领域的单维人工波合成方法,且实现了对峰值速度(PGV)和峰值位移(PGD)的拟合[4-5],但所得地震动实际难以模拟地震动的频率非平稳特性[6],同时受其原理的限制,难以推广到多维。在调整实际地震加速度记录方面,Hancock等[7]通过对实际地震加速度记录叠加小波函数,在保留了其强度和频率非平稳特性的基础上,实现了对目标反应谱的拟合;Mukherjee等[8-9]则分别应用连续或离散小波变换对实际地震加速度记录进行频谱组成和振幅调整,也取得了较好的效果。但上述调整实际地震加速度记录的方法均未给出对PGV、PGD的拟合方式,且仅局限于单维地震波的合成。
由于核电站内、外部的管路系统及安全装置等通常属于中、长周期结构,地震动的PGV、PGD对该类结构动力反应的影响较 PGA 更为直接[2,4-5,10]。为了较全面的评估核电厂结构的抗震安全性,本文在引入基数B-样条小波函数模拟实际多维地震动场的基础上,对调整地震动的时域叠加小波函数法作出改进,用以实现对核电厂多维设计用伪加速度反应谱及PGA、PGV、PGD的同时拟合,以满足核电厂抗震设计规范的需求。
1 多维地震动场的小波模拟方法
本文应用崔锦泰建立的二阶基数B-样条小波函数模拟实际多维地震动场,主要是考虑到其对称性、紧支撑性和线性相位特性适合于处理地震动这类非平稳能量有限信号[9]。
首先将二阶基数B样条函数N2(t)作为尺度函数,构造相应的基数 B样条小波函数 ψ2(t),然后由{2j/2ψ2(2jt-k);k∈Z}线性张成尺度为 j的小波空间 Wj,由多分辨分析的定义,尺度空间Vj与Wj-1有如下关系:

式中:n为Vj分解的层数。基于上述原理,j尺度下的信号aj(t)具有唯一分解:
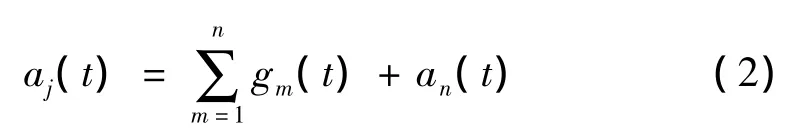
式中:gm(t)代表第m层的高频成分,an(t)代表第n层的低频成分,其表达式如下:
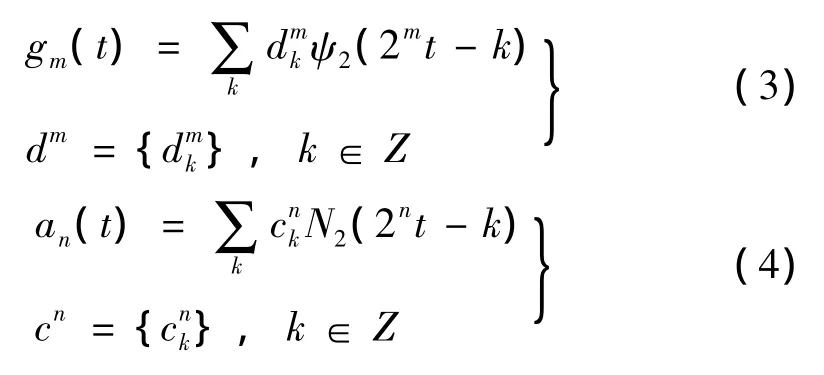
式中:cn,dm分别是第n层、第m层小波系数的集合,k代表在时间轴上的移动尺度。通过上述表达式即可实现将多维地震加速度记录aj(t)在时域和频域同时展开的目的。
通过引入快速分解序列{ak,bk}及双尺度方程系数{pk,qk},即可实现上述变换的分解及重构算法[11-12]。
2 时域叠加小波函数法
时域叠加小波函数法最早由Lilhanand等[13]提出,后来经过Hancock等[7]的一系列改进,使其成为一种高效的调整实际地震加速度记录方法。该小波函数实质是简谐平稳信号,和其它叠加单位脉冲函数的方法一样,都是基于Duhamel积分原理,在时域内直接修改地震加速度记录,通过循环调整使其反应谱和目标谱相协调。
由于核电厂设计用伪速度谱转换为伪加速度谱后不存在平台段,依据反应谱平均值的拟合方法[8-9]不再适用;通过对频率点进行逐个修正的时域叠加小波函数法具有很好的通用性,但缺点是不能实现对PGV、PGD的拟合,且当地震动的采样频率较低时收敛性也较差,实际应用范围受到较大限制。
3 拟合多维目标反应谱及相关峰值的地震动调整方法
根据拟建场地,选择一组与设计基准期内可能发生的地震震级、震中距等因素相近的两水平向及竖向实际地震加速度记录al(t)(l=1,2,3),对其峰值加速度作标准化处理后作为初始地震波。调整的具体步骤如下:
(1)首先将核电厂抗震规范中的水平向及竖向伪速度反应谱SV(w,ξ)转换为伪加速度反应谱SA,target(w,ξ),作为待拟合的目标谱,其中w为待拟合的频率点,ξ为阻尼比。该过程中w应均匀地分布于对数坐标,且不少于规范中要求的76个点。
应用二阶基数B-样条小波函数按式(1)~式(4)模拟和分解实际地震加速度记录al(t),然后根据其反应谱SA(w,ξ)在各周期区间的平均值及目标反应谱值,按式(5)确定各小波分量的调整系数 λA,m(m=1,2,…,n),将各小波系数乘以调整系数后重构,即可实现对目标反应谱和峰值加速度的大致逼近,以确保后续过程的收敛性:
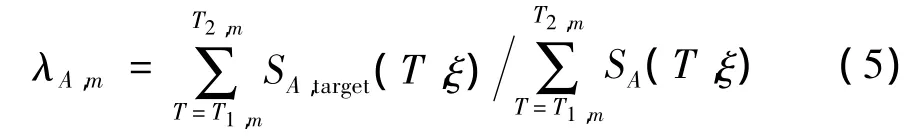
式中:T=2π/w,T1,m和 T2,m分别为第 m 个小波分量所对应的起始周期和结束周期。
(5)依据强震记录及各小波分量的峰值速度及其发生时刻,确定对整体峰值速度贡献最大的小波分量(t)(m=m1~m2)。然后依据目标峰值速度VPG,target与(t)的实际峰值V(t0)及(t)在t0处的速度值Vm(t0)由如下关系确定该小波分量的调整系数:
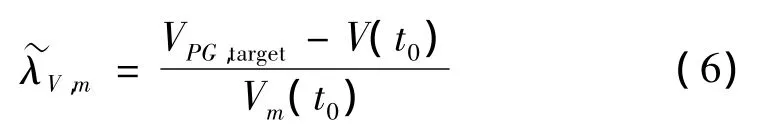
(6)依据强震记录及各小波分量的峰值位移及其发生时刻,确定对整体峰值位移贡献最大的小波分量(t)(m=m1~m2)。然后依据目标峰值 DPG,target与(t)的实际峰值D(t0)及(t)在t0处的位移值Dm(t0)由如下关系确定小波分量的调整系数:
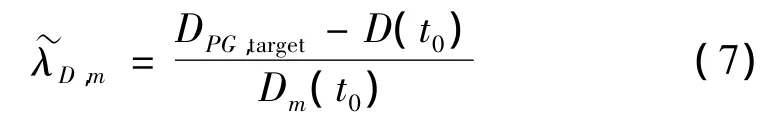
(7)若第(5)、第(6)步的调整过程改变了PGV及PGD的发生时刻,以至于达不到预定值,则对调整后的(t)循环执行第(5)、第(6)步,直到满足PGV及PGD的精度要求为止。
考虑到上述过程中多次用到积分及循环运算,笔者采用了C语言与MATLAB混合编程的方式实现了程序的调试与编制工作,极大的提高了计算效率。当采用其它符合条件的多组实际地震动记录作为初始地震波时,按相同的方法可以得到时频特性不一样,但与核电厂设计用伪加速度反应谱及相关峰值相兼容的多维地震动时程曲线。
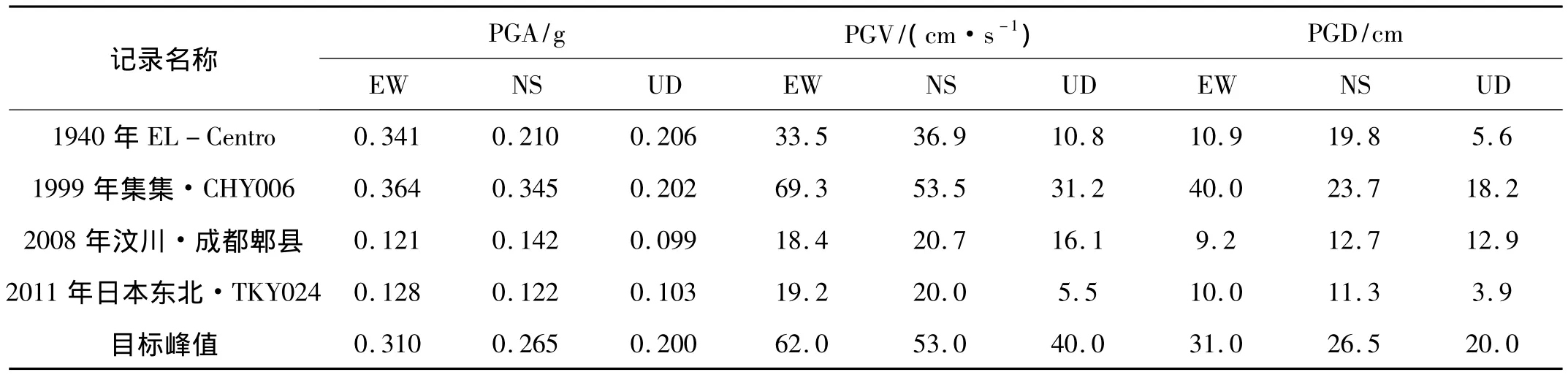
表1 三维实际记录地震波的峰值加速度、峰值速度、峰值位移及目标值Tab.1 The real and target values of PGA,PGV and PGD of three-dimensional ground motions
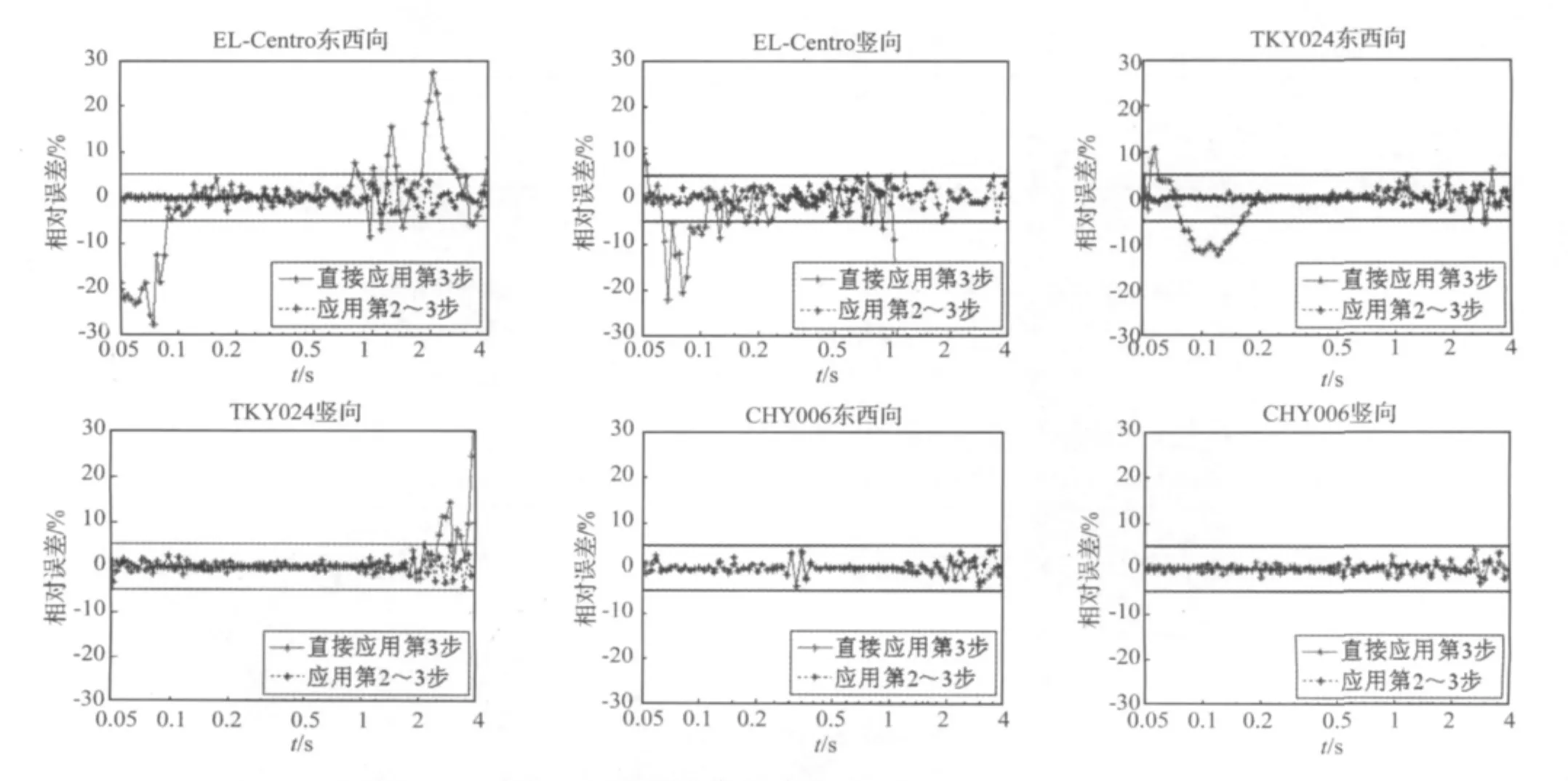
图1 应用第2~3步调整及直接应用第3步调整后的反应谱拟合精度Fig.1 The matching precision after modified by step 2~step 3 and directly by step 3

图2 本文方法调整后(实线)及PGA标准化后(虚线)的加速度、速度及位移时程Fig 2.The acceleration,velocity and displacement time histories after modified by this paper’s method(solid line)and after PGA standard(dotted line)
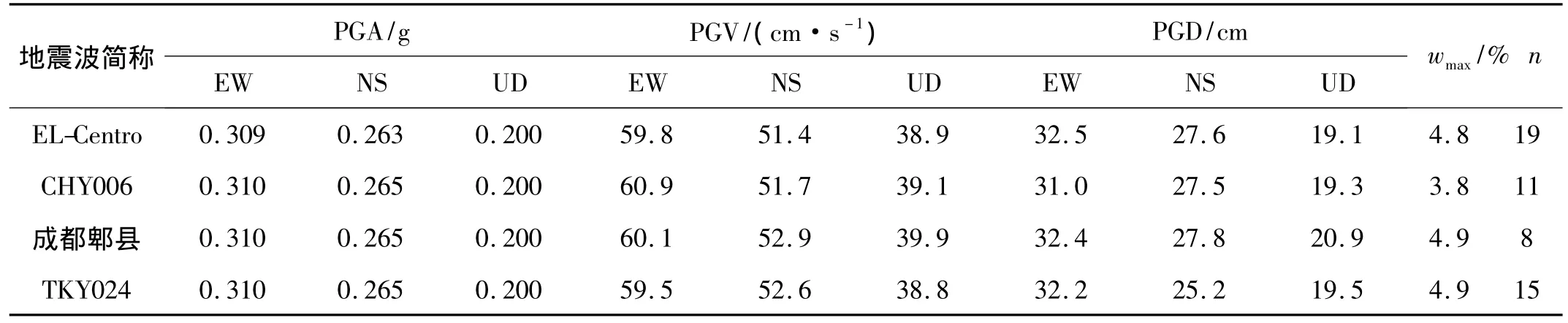
表2 本文调整后的峰值加速度、峰值速度、峰值位移及相对误差最大值、循环次数Tab.2 The values of PGA,PGV and PGD after modified,and max values of relative error,iteration times
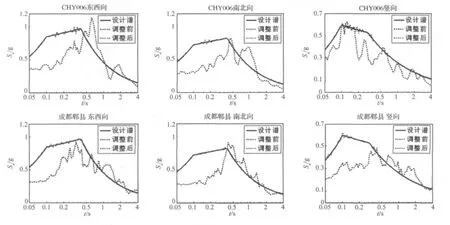
图3 本文方法调整前后伪加速度反应谱及设计反应谱Fig 3.The pseudo acceleration response spectra after modified and the design response spectra
4 算例分析
为对某核电厂进行7度罕遇地震作用下的抗震验算,本文选取四组分别代表不同设计地震分组的三维实际地震加速度记录作为范例(如表1,前两组为近震,后两组为中、远震),拟合我国核电厂抗震设计规范中硬土场地条件下阻尼比为5%的设计用伪加速度反应谱,根据文献[14]的建议设定周期范围为[0.05 s,4 s]。参照我国抗震设计规范和美国ATC-3规范设定水平向、竖向的峰值加速度、峰值速度及峰值位移分别见表1。
根据核电厂抗震设计规范设定100个待拟合的频率点,同时要求反应谱及相关峰值的拟合精度均不应高于5%。首先按本文方法第2、第3步对上述地震波进行调整拟合目标反应谱及峰值加速度,限于篇幅仅作出EL-Centro(采样频率:50 Hz)、TKY024(采样频率:100 Hz)及CHY006(采样频率:250 Hz)地震记录东西向、竖向的反应谱相对误差如图1所示,为进行对比,同时作出不经过第2步处理、直接应用时域叠加小波函数法时的拟合结果。
由图1可知,由于时域叠加小波函数法对频率分辨率的依赖性较强,采样频率较高的CHY006三维数字地震记录具有较好的收敛性,而采样频率较低的ELCentro及TKY024三维模拟地震记录均难以收敛。经过本文方法第2步处理后的模拟地震动记录由于大致逼近了目标反应谱及峰值加速度,整个过程的收敛性得到了较大程度的改善。
在按第4~第6步对各组地震波进行小波分解以确定对峰值速度、峰值位移贡献最大的小波分量后,对上述地震波进行循环调整;调整后的相关峰值及其相对误差最大值wmax、循环次数n如表2所示。由表2可见,近震和中、远震的相关峰值均能满足拟合精度要求,其中峰值加速度的精度最高,峰值速度次之,峰值位移最低;另外由于数字地震记录采样间隔短,积分得到速度、位移时程的精准度高,CHY006及“成都郫县”地震波调整后的相关峰值就整体而言不仅拟合精度要高于模拟地震记录,且收敛速度也相对较快。
CHY006及成都郫县台站(采样频率:200 Hz)三维数字地震波调整前后的加速度、速度及位移时程如图2所示,伪加速度反应谱及目标反应谱如图3所示。由图可知调整后的三维地震动不仅较好的保留了原地震动的局部时频特性,且对多维伪加速度反应谱也具有较高的拟合精度。这说明应用本文方法模拟多维地震动场基本能满足核电厂抗震设计规范的要求。
5 结论
本文引入二阶基数B样条小波函数模拟实际多维地震动场,在对已有的时域叠加小波函数法的收敛性作出改进的基础上,实现了对核电厂多维设计用伪加速度反应谱及相关峰值的同时拟合。
选取了四组实际三维地震动记录分析了该方法的可行性,结果表明该方法对近震和中、远震实测记录均具有较好的拟合效果,能较好的保留原地震记录的局部时频特性。当采用其它实际地震记录时,应用本文方法能给出多组与目标反应谱及相关峰值相兼容的地震动时程曲线,可用于核电厂结构地震作用下的多维动力反应分析。但是应该看到由于地震动各分量之间的关系较为复杂,该方法的广泛应用还有待于多维地震动相关理论的进一步完善。
[1] GB50267-1997,核电厂抗震设计规范[S].国家技术监督局,中华人民共和国建设部,1997.
[2] 胡聿贤.地震工程学(第二版)[M].北京:地震出版社,2006.
[3] 杨庆山,姜海鹏.基于相位差谱的时频非平稳人造地震动的反应谱拟合[J].地震工程与工程振动,2002,22(1):32-38.
[4] 赵凤新,张郁山.拟合峰值速度与目标反应谱的人造地震动[J].核动力工程,2006,28(4):429-437.
[5] 赵凤新,张郁山.拟合峰值位移与目标反应谱的人造地震动[J].核动力工程,2007,28(2):38-41.
[6] 贺 瑞,秦 权.产生时程分析用的高质量地面运动时程的新方法[J].工程力学,2006,8(8):12-19.
[7] Hancock J,Watson-Lamprey J,Abrahamson N A,et al.An improved method of matching response spectra of record earthquake ground motion using wavelets[J].Journal of Earthquake Engineering,2006,10(1):67-89.
[8] Mukherjee S,Gupta V K.Wavelet-based generation of spectrum compatible time-histories[J].Soil Dynamics and Earthquake Engineering,2002,22(9):799-804.
[9] 谢异同,张同亿,吴敏哲.时程分析中设计地震动调整的小波分析方法[J].地震工程与工程振动,2002,3(6):19-23.
[10] Chopra A K著,谢礼立,吕大刚,译.结构动力学:理论及其在地震工程中的应用(第二版)[M].北京:高等教育出版社,2005.
[11] 徐长发,李国宽.实用小波方法(第二版)[M].武汉:华中科技大学出版社,2004.
[12] Chui C K.An introduction to wavelets[M].San Diego:Academic Press,1992.
[13] Lihanand K,Tseng W S.Development and application of realistic earthquake time histories compatible with multidamping design spectra[C].Proceedings of the 9th World Conference on Earthquake Engineering,9WCEE Organizing Committee,Tokyo Japan,Ⅱ,1988,819-824.
[14] 李忠诚,赵凤新.不同法规关于核电厂设计地震动合成的技术要求比较[J].核动力工程,2006,27(2):17-21.
