主被动电磁式动力吸振器及其在桁架振动控制中的应用
2012-09-15杨恺,崔龙,黄海
杨 恺,崔 龙,黄 海
(北京航空航天大学 宇航学院航天飞行器与导弹技术实验室,北京 100191)
为减少发射重量,航天器越来越多的采用桁架等轻质柔性结构。这类结构受到干扰容易引发共振现象,使安装其上的有效载荷不能正常工作,因此针对轻质柔性结构的振动控制受到广泛关注。国内外学者提出采用在结构中嵌入压电陶瓷、磁致伸缩材料等主动控制元件实现被控结构振动控制的方法[1-3]。然而对于航天领域运用的盘压杆、充气结构等变形式展开结构,难以通过直接嵌入主动控制元件的方法进行振动控制,从而限制了这类结构的应用。
对于这类变形式展开结构的振动控制,采用动力吸振器(DVA,Dynamic Vibration Absorber)是一种有效地解决途径。DVA由Ormondroyd等[4]提出,其原理是在结构上附加质量弹簧共振系统,通过该系统在共振时产生的反作用力抑制被控结构的振动。由于DVA具有结构简单,振动控制效果良好的优点,在地面大型结构[5]和航空领域[6]已有应用,国内外也对其振动控制的机理与应用展开了研究,例如:Hugin等[6]提出了一种固有频率可调的半主动DVA,用于直升机的减震控制;Rudinger[7]对一种采用非线性阻尼的被动 DVA进行了建模研究,通过数值仿真验证了这种DVA的振动控制效果;孙志卓等[8]设计了一种基于电磁弹簧原理的动力吸振器,通过动态调节吸振器电磁弹簧刚度实现对各频率的振动抑制,并通过仿真验证该DVA的控制效果。上述DVA均为被动或固有频率可调的半主动吸振器,虽然具有控制简单的优点,但振动控制带宽和控制效果均有限,从而无法满足对宽频振动控制的需求。
为解决航天器轻质柔性结构的宽频振动控制问题,本文提出了一种主被动电磁式动力吸振器,具有被动和主动两种控制模式。吸振器工作在被动模式时,无需外部供电,工作在主动模式时,具备宽频振动控制能力。首先根据电磁式DVA的振动控制原理设计了DVA的结构,并在设计过程中分别对DVA的磁场性质和膜片弹簧进行了有限元分析。随后对研制的DVA实物进行了性能测试,最后以三棱柱桁架为对象,进行了DVA的主被动振动控制实验。
1 电磁式DVA振动控制原理
电磁式DVA由永磁铁、励磁线圈和弹簧组成。永磁铁作为动子,与作为定子的线圈通过刚度为kd的弹簧连接。DVA与被控结构构成的DVA振动控制系统如图1所示。

图1 电磁式DVA振动控制系统的示意图Fig.1 Vibration control system of electromagnetic DVA
设DVA的动子质量为md,其受到电磁控制力为fd、弹簧回复力为 kdxd、电磁阻尼力为fe,则 DVA的动力学方程为:
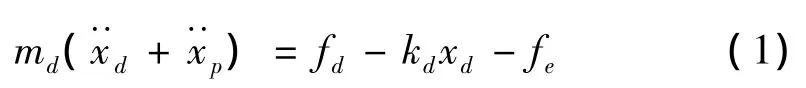
式中:xd和xp分别为动子相对定子的运动位移和被控结构的振动位移。
根据电磁感应原理,fd与fe分别满足:
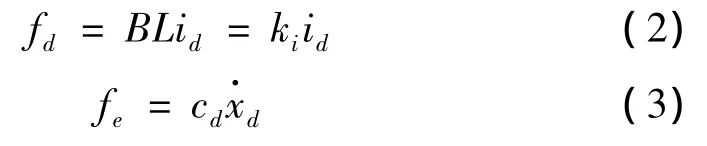
式中:id为线圈电流,B为永磁铁在线圈处的磁场强度,L为线圈总长,ki定义为DVA力常数。cd为电磁阻尼系数,其由永磁铁与定子相对运动形成的电磁涡流效应产生。
DVA工作时对被控结构产生的反作用力P满足:

则被控结构振动控制方程为:

式中:M,K,C分别为被控结构的质量、刚度和阻尼。fv为被控结构受到的干扰力。由式(4)、式(5)知,通过控制线圈电流id,可实现对被控结构的主动控制;当线圈电流id为0时,DVA工作在被动模式,依靠电磁阻尼cd消耗被控结构的振动能量。根据文献[4]的分析,当被动DVA的固有频率与振动频率一致时,DVA动子振幅最大,相位却滞后-π/2,被动振动控制效果最好。
为研究被动DVA的振动控制效果,进行了动力学仿真。仿真参数如下:被控结构质量M为1 kg,固有频率为7 Hz,阻尼C为0.3 Ns/m,受到幅值为1 N的持续干扰力。DVA动子质量 md为0.3 kg,固有频率为7 Hz,电磁阻尼cd为40 Ns/m。
仿真结果显示,相比无DVA,被动DVA对固有频率(7 Hz)附近的振动控制效果最明显,振幅衰减21 dB,即超过90%,对结构的共振模态有明显的抑振效果,对非共振模态的振动控制效果不明显,控制效果有限,需在被动DVA的基础上增加主动控制,以提高抑振能力。
2 电磁式DVA的设计
2.1 DVA结构
电磁式DVA的结构如图2所示,该DVA主要由5个部分组成:① 永磁铁;② 线圈套筒;③ 膜片弹簧;④外壳;⑤ 线圈。永磁铁1与线圈套筒2沿轴向安装在外壳4内。其中,套筒2的凹槽内缠绕直径为0.45 mm的线圈,其内壁与永磁铁1存在δ=1 mm的间隙。永磁铁1的两端分别通过一片膜片弹簧3与外壳4连接,这种安装方式避免了永磁铁在运动过程中发生偏移,从而保证永磁铁始终沿DVA轴向方向运动。当永磁铁1轴向运动时,引起膜片弹簧3的轴向变形,从而产生弹簧回复力。
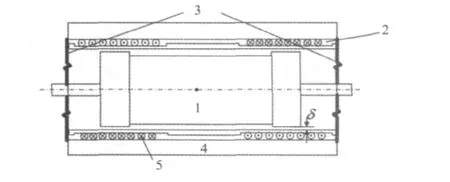
图2 电磁式DVA结构示意图Fig.2 Structure of electromagnetic DVA
由电磁式DVA振动控制原理可知,DVA的磁场分布与膜片弹簧是影响DVA控制性能的重要环节,因此需对这两个环节进行详细设计。
2.2 DVA磁场设计
由式(2)可知,DVA磁场分布决定了DVA力常数ki,从而决定了DVA主动控制性能。因此,对该结构的DVA磁场进行了有限元分析。其中,永磁铁模型的材料为钕铁硼,外壳模型的材料为45钢,线圈的材料为铜,线圈在线圈套筒的每个凹槽上各缠绕了68圈。
分析结果显示:永磁铁产生的磁力线在线圈位置密集分布,磁场强度B介于0.14 T~0.27 T。在该磁场分布下,控制力fd与线圈电流id呈线性关系,DVA力常数ki为1.61 N/A。仿真结果还显示,由于外壳的软磁特性,磁力线被完全封闭在DVA内部。上述分析结果表明,该DVA的线圈电流与其控制力呈线性关系,同时其外壳起到了隔磁作用。
2.3 膜片弹簧设计
由DVA的结构可知,膜片弹簧不仅要为DVA提供轴向刚度kd,还需要横向支撑永磁铁,防止其在运动过程中出现轴向偏移。为使DVA的共振频率与轻质柔性结构的共振频率一致,以达到良好的被动振动控制效果,膜片弹簧的轴向刚度需设计的较低。相反,膜片弹簧的径向刚度却需要设计的较高,以横向支撑永磁铁。因此,设计了如图3所示的膜片弹簧,其外径为50 mm,厚度为0.1 mm。

图3 膜片弹簧有限元模型Fig.3 Finite element model of the membrane
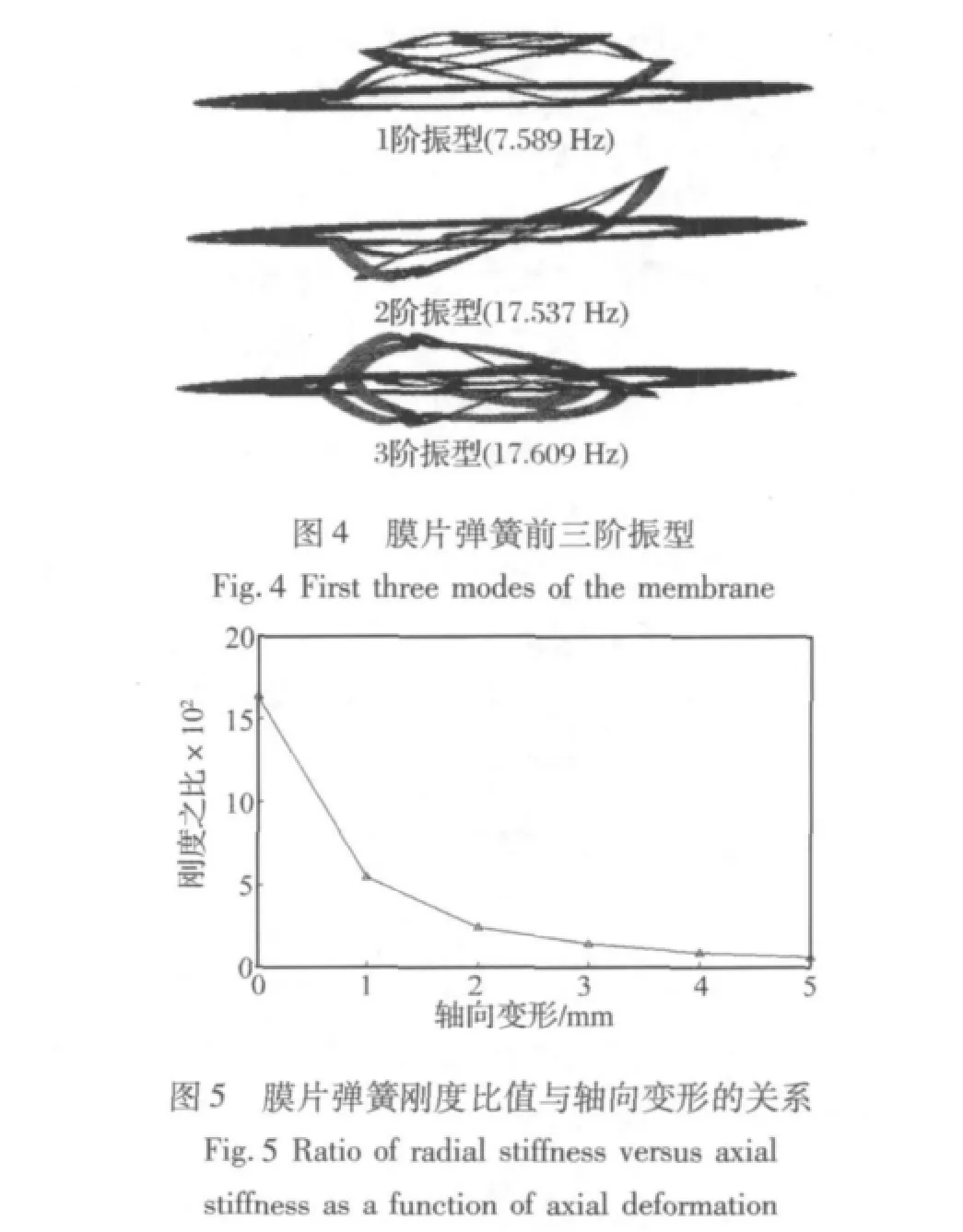
对该膜片弹簧进行了非线性有限元分析,得到了其径向刚度与轴向刚度的比值,以验证膜片弹簧形状的合理性。该膜片弹簧的前三阶振动形式如图4所示。其中,膜片弹簧的材料为304号无磁不锈钢,在分析过程中固定约束弹簧的边缘,以1 mm为间隔依次对弹簧中心加载0~5 mm的轴向变形,分别求得每次加载条件下的径向和轴向刚度。该膜片弹簧径向刚度与轴向刚度比值随轴向变形的变化关系如图5所示。
结果显示,膜片弹簧一阶振型为沿轴向的振动,二、三阶分别为绕径向的弯曲振动。采用两片膜片弹簧对称支撑磁铁,防止磁铁在运动时发生翻转。膜片弹簧的径向刚度与轴向刚度之比随DVA的轴向变形而减小,当轴向变形为0 mm时,径向刚度与轴向刚度之比最大,其比值为1 646;当轴向变形为5 mm时,膜片弹簧的几何非线性变形导致径向刚度大幅降低,此时径向刚度与轴向刚度之比最小,比值为61。分析结果表明,该膜片弹簧的径向刚度比轴向刚度大1个数量级以上,满足设计要求。
根据上述设计,研制了如图6所示的主动电磁式DVA原理样机。该DVA总重量为0.71 kg,最大径向尺寸为54 mm,轴向最长为120 mm。其采用了永磁铁为动子,线圈为定子的动铁式作动方式,更好的利用了永磁铁的质量,较传统动圈式作动方式具有质量更轻的优点,同时避免了可动线圈与外壳的摩擦对振动控制的不利影响。

图6 DVA原理样机Fig.6 DVA prototype
3 DVA的性能测试
由于主动DVA的振动控制效果由控制力fd和作用力P的性能决定,因此针对图6所示的DVA原理样机,进行了上述两种力的实验测试。
3.1 DVA控制力fd的性能测试
以0.3 A为间隔,给DVA线圈依次输入0~1.8 A的恒定电流,通过力传感器测得DVA输出的控制力fd。控制fd与线圈电流 id的关系如图7所示。图中,方块为磁场仿真分析得出的控制力曲线,三角形表示实验中测得的控制力曲线。
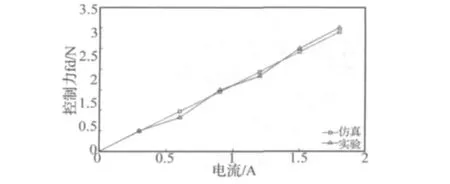
图7 DVA电流-控制力关系Fig.7 DVA control force as a function of current
结果显示,fd与id线性相关度为0.997,线性拟合得到的DVA力常数ki为1.67 N/A,与磁场仿真分析所得的结果相差3.6%。该结果说明,fd与id呈高度线性关系,与仿真结果接近,验证了设计分析的正确性。
3.2 作用力P频响特性
由式(4)知,作用力P为DVA在控制电流id作用下产生的动态力。因此为得到P与id的动态关系,搭建了如图8所示的实验装置。该实验装置由DVA、力传感器、电阻R和LMS振动分析仪组成。其中,DVA固定在力传感器的端部,其线圈与电阻R串联,并与LMS振动分析仪的信号输出端相连。

图8 DVA作用力测试系统Fig.8 Active-force testing system of DVA
实验过程如下:LMS分析仪向DVA输出3~20 Hz等幅值控制信号,通过将电阻R两端的电压信号U反馈给分析仪,以稳定信号幅值。DVA在控制信号作用下,对力传感器产生的动态作用力P,力传感器采集得到P,传输给分析仪。由分析仪得到了如图9所示的P在控制电流id作用下的频率响应曲线。图9(a)为作用力P随在控制电流id作用下的幅频曲线,图9(b)为P在id作用下的相频曲线。

幅频响应结果显示,当id的频率低于7 Hz时,DVA作用力P随着控制电流id的频率增加而迅速增大,当频率超过7 Hz以后,P增幅平缓,逐渐趋于稳定。在实验过程中,作用力P未出现共振峰值。相频结果显示,P与id的相位差随频率的增加而减小,在7.4 Hz处穿越90°。测试结果表明,DVA的固有频率为7.4 Hz,其阻尼比大于1,在被动工作模式下,该DVA针对7.4 Hz附近的振动具有良好的控制效果。
4 DVA-桁架振动控制实验
为验证本文设计的DVA主被动振动控制效果,将DVA安装在一三棱柱桁架结构顶端,构成DVA-桁架振动控制系统,进行了振动控制实验。
4.1 DVA-桁架振动控制系统
DVA-桁架振动控制系统如图10所示,系统由三棱柱桁架、压电作动器、DVA、加速度计、功率放大器和dSPACE1105控制器组成。实验中采用的三棱柱桁架结构的一阶模态频率为7Hz,振动形式为相对桁架根部的弯曲振动。DVA固定在桁架顶端,其轴向方向沿桁架顶部振动幅度最大的方向。扰源为桁架底部的一根压电陶瓷,通过dSPACE1105控制器产生持续的信号,驱动压电陶瓷产生干扰力,以模拟桁架受到的外扰。该实验的主动振动控制器也采用dSPACE1105实现,通过控制算法计算并输出控制电压,再经功率放大器以1.5 A/V的比例转化为DVA的控制电流。桁架顶端的振动加速度由加速度计测量,经信号调理器双积分后得到振动位移,然后输入到dSPACE1105中。
该振动控制实验的工作原理:桁架底部受到持续的扰动力fv而引起振动,控制器将顶端振动位移xp作为控制器的输入信号,通过振动控制算法计算并输出控制电流id,使DVA对桁架产生反作用力P,实现对桁架的振动控制。

图10 DVA-桁架振动控制实验系统Fig.10 DVA-truss vibration control system
本文采用的振动控制算法为Christian提出的ADC(Adaptive Disturbance Canceller)算法[9],该方法将与干扰频率相同的单位正余弦信号作为基底信号,通过各自乘以自适应调节的比例系数,构造成DVA的控制信号,使DVA对桁架产生与干扰力fv作用相反的作用力P,实现对桁架的振动控制。其控制原理如图11所示。其中,通过归一化最小均方根算法(Normalized Least Mean Square,nLMS)[10]实现对比例系数的自适应调节。

图11 ADC控制原理图Fig.11 ADC Schematic diagram


式中,U=[u1,u2]T为 nLMS算法的输入,即第 n次采样时刻的基底信号,δ为收敛调整系数。控制电流id产生作用力P,在P的作用下,桁架顶端产生的振动位移为:
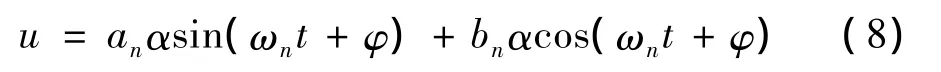
式中,α,φ分别为电流id在ωn的频率处,经过DVA和桁架环节后的增益与相位差。
通过式(7)自适应调整an和bn,改变u的幅值和相位,使u与干扰力激起的振动位移 v的幅值相等,方向相反,从而使xp→0,实现抑制振动。
4.2 控制实验及结果
本实验的ADC算法参数设置如下:迭代步长μ=5×10-4,收敛调整系数 δ=1 ×10-10,权系数 an,bn的初值均为0。
首先针对桁架的共振模态(7 Hz)振动进行了控制实验。前5 s DVA工作在被动模式,第5 s时开启主动控制。振动控制效果及主动控制电压如图12所示。图12(a)中,实线表示采用DVA进行主被动振动控制时桁架的顶部位移曲线,虚线代表无DVA时桁架的顶部位移曲线。

图12 振动控制结果与控制电压Fig.12 Vibration control results and Control voltage
结果显示,DVA工作在被动模式,桁架顶部振动位移xp的振幅由5.41 mm衰减至2.66 mm,衰减幅度为50.83%。开启主动控制后,振幅进一步衰减,最终衰减为0.2 mm,衰减幅度达96.30%,dSPACE输出的最大控制电压为0.2 V。实验结果表明,主被动DVA对桁架共振模态的振动控制均有显著的效果,而主动DVA控制效果明显优于被动DVA。
将干扰力fv的频率变为10 Hz,以测试DVA对桁架非共振模态振动的控制能力。将对桁架的干扰力幅值增加10倍,使桁架顶部产生明显的振动。在第5 s开启主动控制,其振动控制效果如图13所示。图中,实线表示有DVA时桁架的顶部位移曲线,虚线表示无DVA时桁架的顶部位移曲线。
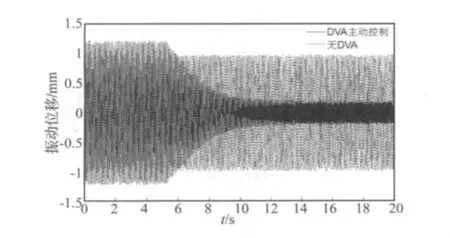
图13 有无DVA对非共振模态振动的主动控制结果Fig.13 Non-resonant vibration control results with/without DVA
结果显示,采用DVA的主动控制后,桁架顶部振动位移的幅度在14 s左右由0.97 mm降至0.18 mm衰减达81.40%。实验结果表明,DVA主动控制针对桁架非共振模态振动依然拥有明显的控制效果。
5 结论
为解决轻质柔性结构的振动控制问题,本文提出了一种主被动电磁式动力吸振器。通过仿真分析与实验结果得到了以下结论:
(1)本文设计并研制的主被动电磁式DVA具有零部件少,结构简单的特点。由性能测试结果可知,DVA的电磁控制力与控制电流呈高度线性关系,主动控制律简单。该DVA的固有频率为7.4 Hz,其阻尼比大于1,对7.4 Hz附近的振动具有良好的被动抑振效果。
(2)由对三棱柱桁架振动控制的实验结果可知,被动DVA对桁架共振模态的振动有50.83%的抑制效果,而采用ADC振动控制算法的主动DVA对结构共振和非共振模态的振动控制效果分别达96.30%和81.40%,抑振效果明显。
本文研制的主被动电磁式DVA可作为多自由度动力吸振装置的一个组件,用于抑制柔性结构的多模态振动,在航天振动控制领域将具有广阔的应用前景。
[1] Chopra I.Review of state of art of smart structures and integrated systems[J].AIAA Journal,2002,40(11):2145-2187.
[2] Hyde T T,Anderson E H.Actuator with built-in viscous damping for isolation and structural control[J]. AIAA Journal,1996,34(1):129-135.
[3] 赵国伟,黄 海,夏人伟.柔性自适应桁架及其振动最优控制实验[J].北京航空航天大学学报,2005,31(4):434-438.
[4] Ormondroyd J,Hartog D.The theory of the dynamic vibration absorber[J].ASME Journal of Applied Mechanics,1928:A9-A22.
[5] Soong T T,Spencer B F.Supplemental energy dissipation:state-of-the-art and state-of-the-practice[J].Engineer-ing Structures,2002,24:243-259.
[6] Hugin C,Hatch C.Global control of helicopter vibrations using a semi-active vibration control system[A].AIAA.47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics,and Materials Conference[C].Newport,Rhode Island:AIAA,2006:1860-1867.
[7] Rudinger F.Tuned mass damper with nonlinear viscous damping[J].Journal of Sound and Vibration,2004,300:932-948.
[8] 孙志卓,王全娟,王付山.一种主动电磁式动力吸振器的研究与设计[J].振动与冲击,2006,25(3):198-201.
[9] Taranti C G R.A computationally efficient algorithm for disturbance cancellation to meet the requirements for optical payloads in satellites[D].California:Naval Postgraduate School,2001.
[10] Farhang-Boroujeny B. Adaptive filters:theory and applications[M].New York:John Wiley& Sons,1998.86-120.
