二维滤波器分布式算法结构的改进与实现❋

凌春丽,刘云飞,姜黎黎,李湘云

(南京林业大学 信息科学技术学院 ,江苏 南京 210037)

有限长单位冲激响应(FIR)数字滤波器因其良好的线性相位及稳定性被广泛应用于现代电子通信系统中.设计 FIR滤波器最初采用卷积型、直接型结构,需要组合多个加法器、移位器和乘法器来实现.由于乘法器占用资源太大,相继提出了应用移位相加单元来替代直接型中的乘法器,然而此种结构对现场可编程门阵列(FPGA)的资源利用率仍然太低.为解决这一问题,研究人员提出了许多解决方案,概括起来主要有以下两类方法[1]：

一类是利用二进制编码特性,采用加法器代替乘法器,通过对滤波器系数进行分解,重复使用相同系数因子的简化加法器图(RAG)算法;另一类是应用预先存储或查找表(LUT)方法减少乘法器的使用.此类方法的代表就是分布式(DA)算法.

DA算法因其高效的资源利用率和面积-时间效率得到广泛应用.基于 DA算法的 FIR数字滤波器设计得到广泛应用.主要包括对一系列 LUT的访问和移位累加操作.但随着滤波器阶数的增加,需要的 LUT存储器资源成指数增加,为解决此问题,Wang Sen和 Tang Bin提出了一种应用选择器实现查找表的改进分布式算法[2,3].另外,Meher等人采用对滤波器系数的 bit序列进行并行处理的方法,设计出了一维和二维的 DA算法滤波器,进一步提高了资源利用率和运行速率及数据的吞吐量[4,5].本文在 Meher等人提出的结构上增加了延时模块,避免了因时序设计带来的混乱,保证了输出结果的正确性.同时应用二进制位权乘法(*2n)替代移位相加结构,以节省更多的存储器资源和逻辑单元(LE).

1 二维分布式算法的改进

1.1 分布式算法

一个 N阶的 FIR滤波器的表达式如下：

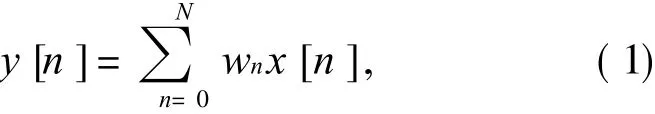
式中：wn表示滤波器系数;x[n]为输入数据.

对于有符号的系统,x[n]可用式(2)表示

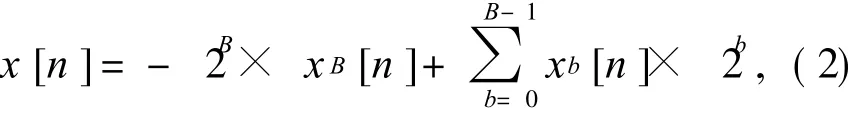
将式(2)代入式(1),得到 DA算法的表达式

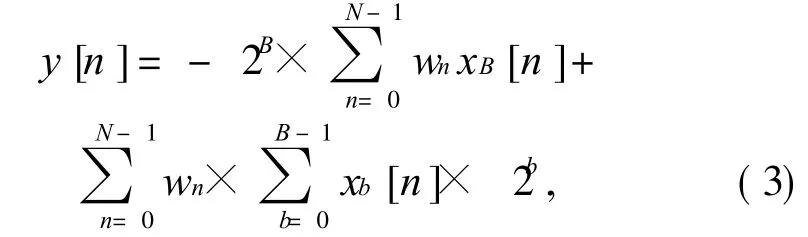
式中：x[n]为输入信号 x的采样序列;y[n]为输出序列;wn为滤波器系数;b表示输入数据的第b个 bit位.

由公式(3)可以看出,分布式算法应用了移位相加单元和加法单元实现乘法.具体计算为：对x0[n]到 xB-1[n],依次乘以 20位权到 2B-1位权;对于符号位 xB[n]乘以 -2B位权.

1.2 二维 DA算法的改进

2008年,Meher设计出了一维和二维的基于DA算法的 FIR滤波器,其中二维的 DA算法如公式(4)[5]

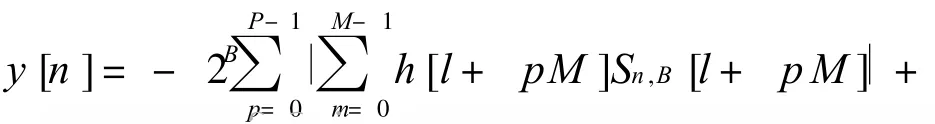
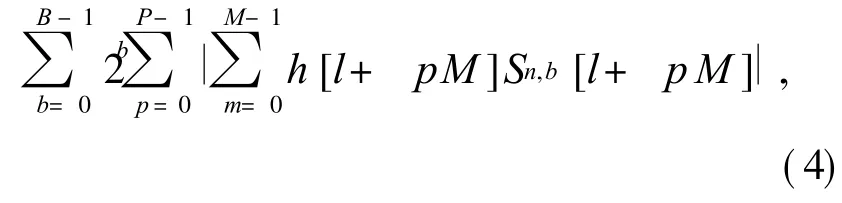
式中：b为输入数据的第b个比特位;B为输入数据的总比特位;n为第n个数据;(N+1)/2=P*M(M为查找表的输入位数;P为每一并串转换下查找表的个数).

Meher设计的二维 DA算法 FIR滤波器的结构[3]与图 1相比缺少了延时模块.采用全局时钟时,时序上有缺陷.以 16阶 FIR滤波器为例,16个输入数据从移位寄存器同时经过并串模块、查找表模块和加法模块.在进入移位相加模块前,16个数据已准备就绪,需在一个周期内对 16个数据同时处理(避免与下一个周期的数据冲突).而 Meher设计的移位相加是以从下(b=7)向上(b=0)的顺序依次执行,无法在一个周期内对 16个输入数据进行处理.若在移位相加模块前增加延时模块,就能保证输出结果的正确性.因此,在Meher提出的结构上增加了延时模块,如图 1所示.将其称之为“延时型”结构.

图1 延时型结构Fig.1 Structure of time-delaying type

Meher等人提出的二维分布式算法结构,对每个系数的 bit序列进行并行处理.Meher提出的移位相加模块从 xB[n]开始,先左移一位(乘2,若为符号位则乘 -2),再加上 xB-1[n];接着将其和再左移一位(乘 2),加上 xB-2[n].如此顺序运算,从下到上,求得结果.此移位相加法可以有效地减少存储器的使用.但由于延时模块的加入,使用了太多的移位器,抵消了移位相加模块节省的存储器资源.为减少存储器资源和 LE的消耗,对延时和移位相加模块进一步优化.这里应用二进制位权乘法(*2n)替代图 1所示的延时和移位相加模块[6],改进后的结构如图 2所示.较之“延时型”结构,“改进型”结构能节省更多的LE和存储器资源.

图2 改进型结构Fig.2 Structure of improv ement type

2 性能分析

为了能更好地观察 P(每一并串转换下查找表的个数)及 M(查找表的输入位数)对 FPGA资源利用率和存储器的影响,分析两种结构的优缺点,本文设计了不同阶数的Ⅱ 型 FIR滤波器以比较其性能[7,8].滤波器阶数取为 3,7,15,31,63阶,将滤波器系数乘以 214,取整,滤波器输入采用了14 bit.分别针对式(4)中的 M=2,4,8的情况进行设计.表 1记录了不同阶数、不同查找表位数下逻辑单元和存储器的消耗情况及滤波器的工作速度.

从表 1可以得出如下结论：①应用 FPGA实现低阶 FIR滤波器时,“改进型”比“延时型”节约了更多的逻辑单元与存储器资源.这是由于在低阶时“延时型”结构中延时模块占用资源较多,甚至超出了移位相加模块所节省的加法器和乘法器资源;② 增加滤波器的阶数,两种结构的存储器和 LE资源会非线性地增加.比较发现,“延时型”消耗 LE资源的增速比“改进型”缓慢.产生这种结果的原因是：当滤波器阶数不断增加,规模不断扩大时,延时模块对 LE消耗的影响越来越小.③滤波器阶数较低时,“延时型”比“改进型”工作速度更快.随着阶数的增加,“改进型”滤波器比“延时型”滤波器工作速度更加稳定,且衰减趋缓.

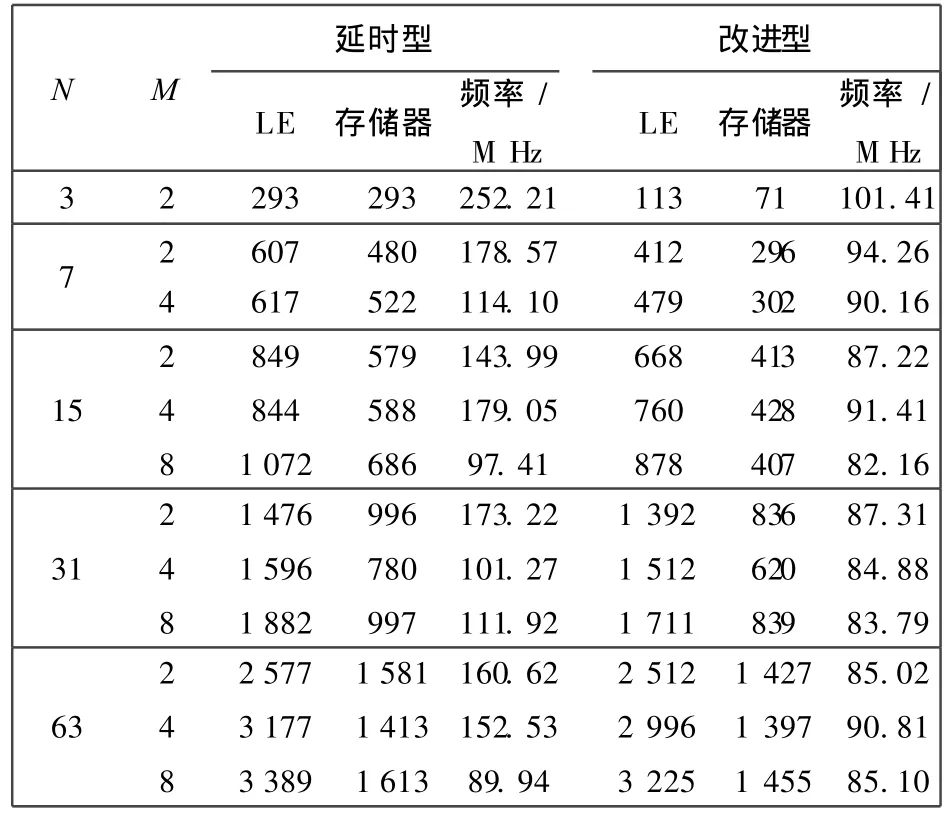
表1 逻辑单元和存储器的消耗情况Tab.1 Consumptions of LE and memory(B=8)

3 仿真结果及硬件实现

3.1 Ⅱ类线性相位FIR滤波器

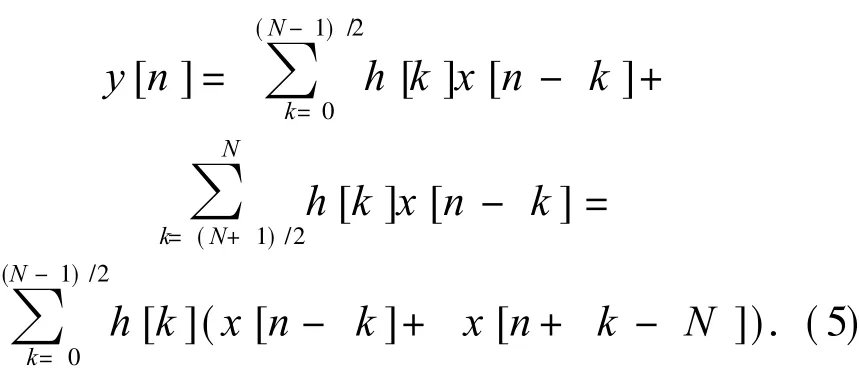
Ⅱ 型 FIR滤波器的表达式为

从式(5)可以看出,由于Ⅱ 型 FIR滤波器的滤波系数为偶对称,一个 N阶的Ⅱ 型 FIR滤波器可以用一个(N+1)/2阶的滤波器实现.相对于非对称 FIR滤波器,式(5)增加了(N+1)/2的加法器及相应的控制逻辑,但是相对于滤波器阶数减少 50%所节省的资源是值得的[9,10].

3.2 滤波器设计与实现

下面以基于“改进型”结构的 31阶 FIR带通滤波器为例,说明滤波器的设计与实现[11,12].

3.2.1 设计指标

采样频率：50 M Hz;类型：带通滤波器;通带范围：250 k～ 800 kHz;输入数据宽度：14位;输出数据宽度：28位.

根据设计指标,应用 MAT LAB软件中的Toolbox工具箱,选择 Hann窗设计符合要求的FIR滤波器系数[4].应用 M ATLAB中的取整函数对系数进行量化,即乘以 214,系数如下：

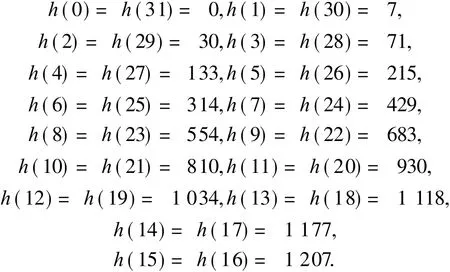
3.2.2 硬件实现

硬件平台采用 Altera公司的 DE2开发板及其配套 AD/DA子板.

软件仿真平台采用 QUARTUS II中的SignalTap.值得注意的是,应用 SignalTap仿真之前必须将滤波程序下载到 DE2开发板上.

应用“一分二”电视分配器合成一叠加信号,此时分配器原有的两个输出端现用作输入端,原输入端现用作输出端.借助两个函数信号发生器产生两路输入信号,其中之一为幅度 2 V的500 kHz正弦信号,另一个为幅度 2 V的 3 MHz正弦信号.将此叠加信号用作滤波器的输入信号.图 3为示波器显示的输入信号.

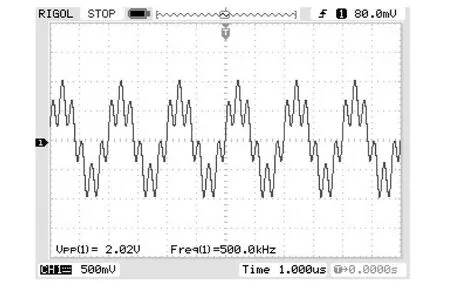
图3 输入信号Fig.3 Input signal

实际测试时,先应用 SignalTap观测仿真效果,如图 4所示.其中 ADC_ DA 为叠加的输入信号,DACDA 为基于“改进型”滤波器的滤波结果.从图 4中可以看出,滤波后的信号频率为500 kHz(周期为 2μ s),没有出现失真,仿真结果符合设计要求.

为验证“改进型”FIR带通滤波器的实际滤波效果,首先将滤波程序下载到 DE2开发板的FPGA芯片上,构成一硬件滤波器,然后将叠加的输入信号通过该滤波器,以实现滤波功能.图 5为叠加信号经滤波后在示波器上的输出,它是一频率为 500 kHz的带内信号,滤波效果与仿真结果一致.

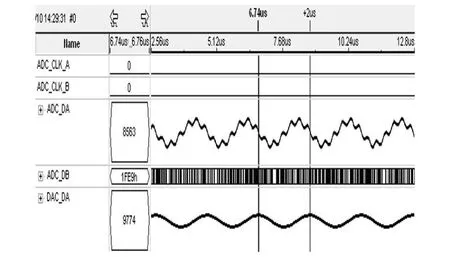
图4 SignalTap仿真图Fig.4 Simulation result using SignalTap

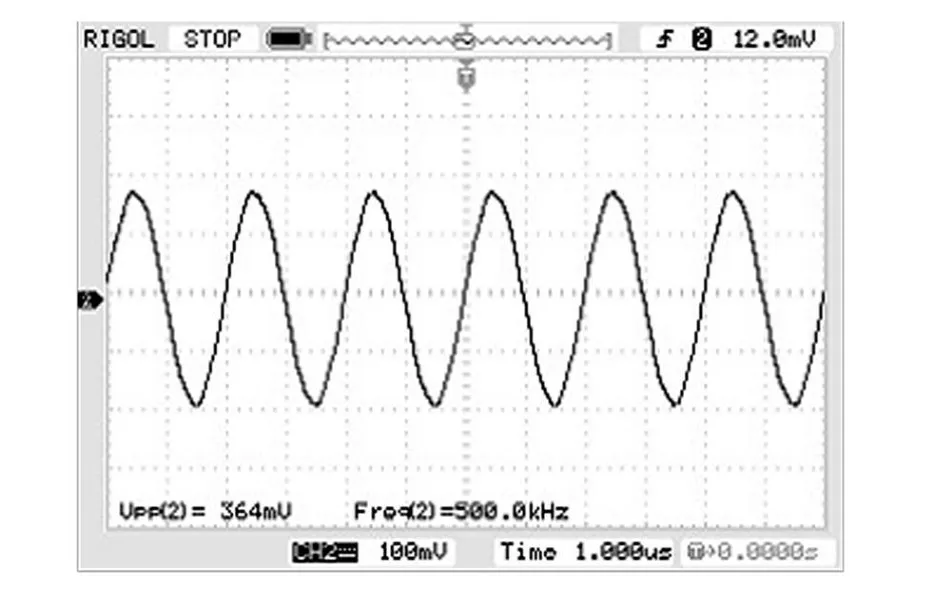
图5 滤波后的输出信号Fig.5 Filtered output sig nal

将幅度 2 V的 500 kHz方波信号与幅度 2 V的 3 MHz方波信号叠加,用作滤波器的输入信号.滤波结果如图 6所示.

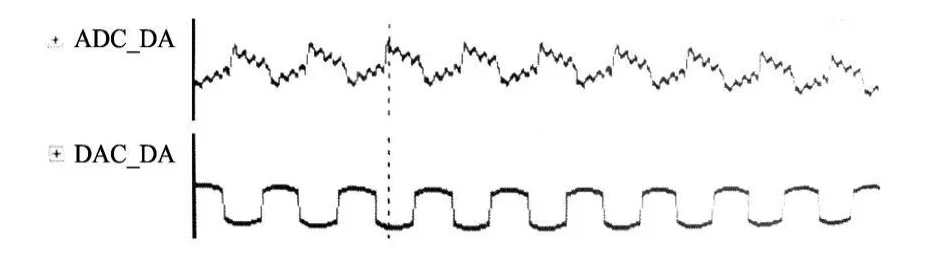
图6 输入信号为方波时的滤波结果Fig.6 Filtering result using square wav es as input signal

4 结束语

文中对 Meher提出的 FIR滤波器结构进行了改进,通过增加延时模块,克服了 Meher设计中时序上的缺陷,并应用二进制位权乘法(*2n)替代延时和移位相加结构,在低阶时节省了较多的 LE和存储器资源.

通过测试不同阶数滤波器的 LE及存储器资源的消耗发现：“延时型”结构和“改进型”结构的FIR带通滤波器存储器资源的消耗并不与查找表位数成线性关系,M=4时较之 M=2和 M=8时能节省更多的存储器资源;LE消耗与查找表位数成正比,M越大,LE消耗越多;“改进型”结构的速度虽然不及“延时型”,但随着阶数的增加,“改进型”结构的滤波速度平稳、衰减缓慢.因此,针对具体设计要具体分析,选择合适的优化结构[14,15].

为验证“改进型”FIR滤波器的设计效果,应用 Altera DE2开发板及其配套的 AD/DA子板进行了测试.测试结果表明：该滤波器完全滤除了通带外信号,实现了带通滤波的目标.

[1]Huang W,Anderson D V.Modified sliding-block distributed arithmetic with offset binary coding for adaptive filters[J].Journal of SignalProcessing Systems,2011,63(1)：153-163.

[2]田丰,牟卫华 ,陈华明,等.基于分布式算法的线性相位 FIR滤波器设计 [J].舰船电子工程 ,2010(2)：57-60.Tian Feng,Mou Weihu,ChengHuaming,et al.Design oflinear FIR filter based on distributed arithmetic[J]. Ships Electronic Engineering,2010(2)：57-60.(in Chinese)

[3]闫永鹏,于海勋.一种基于 LUT的改进 FIR滤波器的设计 [J].微电子学,2010,40(5)：693-696.Yan Yongpeng,Yu Haixun.An improvement design ofLU T-based FIR filter[J].Micro Electronics,2010,40(5)：693-696.(in Chinese)

[4]李书华,曾以成.基于分布式算法的高阶 FIR滤波器及其 FPGA实现 [J].计算机工程与应用,2010,46(12)：136-138.Li Shuhua,Zeng Yicheng.Implementation of highorder filterbased on FIR filteron FPGA[J].Computer Engineering and Applications,2010,46(12)：136-138.(in Chinese)

[5]M eher P K.New approach to LUT implementation and accumulation formemory-based multiplication[C].Proc.IEEE Int.Symp.Cire.and Syst.,2009：453-456.

[6]MeherP K. FPGA realization ofFIR filters by efficient and flexible systolization using distributed arithermetic[J]. IEEE Transactionson Signal Processing,2008,56(7)：3009-3017.

[7]薛严冰,韩雪,邵远.基于分布式算法的 FIR数字滤波器的 FPGA实现 [J].大连交通大学学报,2009(4)：84-87.Xue Yanbing,Han Xue,Shao Yuan.Implementation of digital FIR filter on FPGA based on distributed arithmetic[J].Journal of Dalian Jiao-tong University,2009(4)：84-87.(in Chinese)

[8]王法栋,刘宇.高阶数字滤波器分布式算法结构比较[J].声学技术,2009(3)：307-311.WangFadong,Liu Yu.Comparison of high-order digital filter based on distributed arithmetic[J].Acoustic Technology, 2009(3)：307-311.(in Chinese)

[9]Lo H J,Yoo H J,Anderson D V.A reusable distributed arithmetic architecture for FIR Filtering[J].IEEE,2008：233-236.

[10]Wang Sen,Tang Bin,Zhou Jun.Distributed arithmetic for FIR filterdesign on FPGA [J].International Conference on Communications,Circuits and Systems,2007(10)：620-623.

[11]李林.利用 DA算法实现大规模 FIR滤波器 [J].实验科学与技术 ,2006(2)：7-9.Li Lin.Implementation of large-scale FIR filter using distributed arithmetic[J].Experimental Science and Technology,2006(2)：7-9.(in Chinese)

[12]Rawski M.Efficient implementation of digital filters with use of advanced msynthesis methods targeted FPGA architectures[C].Proceedings of the20058th Euromicro Confenrence on Digital System Design,2005.

[13]张庆玲,杨勇.FPGA原理与实践[M].北京：北京航空航天大学出版社,2006.

[14]刘圆,黄晨灵,高佩君.基于分段查找表的高速 FIR滤波器的设计实现 [J].微电子学,2006,36(5)：674-678.Liu Yuan,Huang Chenling,Gao Peijun.Re-alization of high-speed filter based on sub-LU T[J].Micro Electronics,2006,36(5)：674-678.(in Chinese)

[15]丁丹.FIR滤波器的 FPGA高效实现和巧妙验证[J].电子科技 ,2005(9)：29-32,Ding Dan. Efficientimplementation and clever verification of FIR filter on FPGA[J].Electronic Technology,2005(9)：29-32.(in Chinese)