因题而异设未知数

☉江苏省淮安市淮阴区开明中学 马先龙

在中考选择题和填空题解题中，常常会碰到计算问题.对于此类问题，有时需要列方程（组）解决.列方程（组）前，若能根据题设和图形特点，因题而异设未知数，往往能化难为易，事半功倍.现举例说明如下.

1.直接设未知数

例1 （2011四川内江中考）如图1，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E，那么点D的坐标为（ ）.

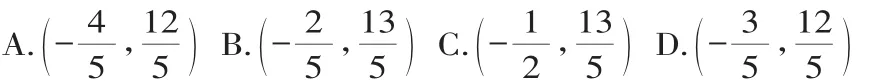
分析：如图1，由条件，易知AD=AB=3，CD=CB=1，过点D分别作DF⊥x轴，DG⊥y轴，垂足分别为点F、G，设D（m，n），在Rt△ADF和Rt△CDG中，由勾股定理易得关于m、n的方程组，解出m、n即可得到点D的坐标.

2.间接设未知数

例2 （2011安徽芜湖中考题改编）如图2，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC，并且AE=6，EF=8，FC=10，则正方形ABCD的面积为________.

分析：如图2，直接求正方形ABCD的面积比较困难，可间接设未知数.

由正方形的面积公式，知只须求出AB的长，因AC=所以只须求出AC的长.连接AC，设AC与EF相交于点G，则AC=AG+CG.由条件易知△AEG∽△CFG，设EG=x，根据相似三角形的性质，可得关于x的方程，解出x，即得EG、FG的长，进而运用勾股定理可求出AG、CG的长，得出AC的长后，问题迎刃而解.

解：如图2，连接AC，设AC与EF相交于点G，设EG=x.

因为AE⊥EF，EF⊥FC，所以∠AEG=∠CFG=90°.

所以AE∥CF，所以△AEG∽△CFG.

所以S正方形ABCD=（4）2=160，所以正方形ABCD的面积为160.

例3（2011重庆市中考）某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成，乙种盆景由10朵红花和12朵黄花搭配而成，丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花，3750朵紫花，则黄花一共用了________朵.

分析：直接求黄花的总朵数比较困难，可间接设未知数.设步行街摆放甲、乙、丙三种造型的盆景分别为x盆、y盆、z盆，则由题意可列出关于x、y、z的方程组，把x当做已知数，从中解出y、z，代入24x+12y+18z中，消去x，即可求出黄花的总朵数.

解：设步行街摆放甲种造型的盆景x盆，乙种造型的盆景y盆，丙种造型的盆景z盆，由题意，得：

3.多设未知数

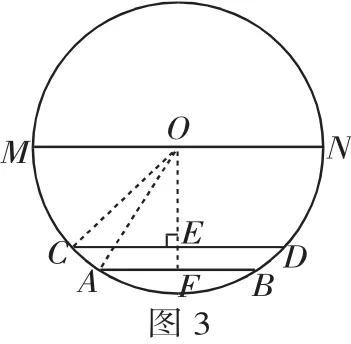
例4（2011四川南充中考）如图3，在圆柱形油槽内装有一些油，截面如图3，油面宽AB为6分米，如果再注入一些油后，油面AB上升1分米，油面宽变为8分米，圆柱形油槽直径MN为（ ）.

A.6分米 B.8分米 C.10分米 D.12分米

分析：如图3，过点O作OE⊥CD，垂足为点E，延长OE交AB于点F，则OF⊥AB，连接OA、OC，则CE=4，AF=3，EF=1.因⊙O的半径和OE都是未知的，所以可多设未知数，设⊙O的半径=x，OE=y，这样就能较容易地列出方程，解出x，则MN=2x.

解：如图3，过点O作OE⊥CD，垂足为点E，延长OE交AB于点F，则OF⊥AB，连接OA、OC，设⊙O的半径=x，OE=y，在Rt△OCE中，由勾股定理，得x2=y2+42……（1）.

在Rt△OAF中，由勾股定理，得x2=（y+1）2+32……（2）.

比较（1）、（2），得y2+42=（y+1）2+32，解得y=3，把y=3代入（1），得x=5，所以圆柱形油槽直径MN为10，应选C.

4.设辅助未知数

例5 （2011浙江温州中考题改编）如图4，八个全等的直角三角形拼接后得到三个正方形.记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3=11，则S2的值为_______.

分析一：如图4，直接求S2比较困难，根据题设和图形的特点，可设每个直角三角形的面积为S（S为辅助未知数），这样就易于找出S1、S2与S和S3之间的关系，把所得关系代入条件，可得S3与S的关系，把这一关系代入S2，消去S即得S2的值.

解：如图4，设每个直角三角形的面积为S.

则S1=8S+S3，S2=4S+S3.因为S1+S2+S3=11，

所以（8S+S3）+（4S+S3）+S3=11，12S+3S3=11.

解：如图4，设每个直角三角形较长的直角边为a，较短的直角边为b，则AB=a+b，EF=，MN=a-b，所以S1=（a+b）2，S2=a2+b2，S3=（a-b）2.

因为S1+S2+S3=11，所以（a+b）2+（a2+b2）+（a-b）2=11，展开整理，得3（a2+b2）=11.