考虑THM的管网水质服务水平多目标优化

虞介泽，李 聪，张土乔，毛欣炜

（浙江大学 建筑工程学院，杭州310058）

供水管网采用二次加氯能提高余氯的均匀性和稳定性，并能减少氯的消耗［1］。为评价不同余氯浓度的 消 毒 能 力 和 嗅 味 影 响，Tamminen 等［2］将Coelho提出的服务水平概念运用到二次加氯评价中，建立了余氯服务水平评价函数。此评价函数量化了余氯在管网中的消毒和减少嗅味的能力，帮助决策者得到管网较优的余氯服务水平。以往的研究表明，加氯消毒会产生消毒副产物（DBPs），加大致癌风险［3］。单独提高余氯的服务水平会增加消毒副产物的浓度。学者们对消毒副产物进行了广泛的研究，并提出了多种生成模型［3］。Carrico等［4］采用基于余氯消耗的THM线性生成模型对二次加氯下的THM生成进行了模拟，得到了不同方案下的THM浓度。为同时优化余氯和THM服务水平，参照Tamminen等的余氯服务水平评价函数，以典型消毒副产物THM为研究对象，提出THM服务水平评价函数，并建立了以管网余氯服务水平最大化、THM服务水平最大化及加氯费用最小化的多目标优化模型。通过EPANET＿MSX模拟余氯衰减和THM生成，利用实数编码的非支配排序遗传算法Ⅱ（NSGA Ⅱ）得到最优Pareto前沿面。考虑主体水余氯衰减系数、基于余氯消耗的THM生成比例系数、出厂水THM浓度、加氯点数量4个影响因素对优化结果Pareto前沿面的影响，为二次加氯提供决策支持。

1 服务水平评价函数

根据Tamminen等［2］对服务水平的描述，对于任意水质监测项目（如余氯浓度、THM等），服务水平可分为5个等级，依次为［2］：100%为最优的服务水平、75%为能满足需求的服务水平、50%为仅能接受的服务水平、25%为不能接受的服务水平、0%为没有服务的水平。根据水质规范规定的最大浓度或最小浓度，以及嗅味浊度等物理指标，采用线性函数来定义服务水平评价函数。

对于余氯，Tamminen等［2］采用如下线性函数定义服务水平：

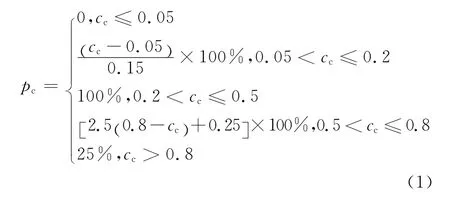
式中cc为余氯浓度，mg／L。

对于THM，若浓度高于规范规定的70μg／L，则其致癌能力很强，服务水平为0%。King等［5］调查了加拿大安大略湖地区膀胱癌发病率和THM间的关系，认为THM浓度在0～24μg／L时持续接触THM 30a以上与膀胱癌的发病无相关性。Do等［6］在THMs对胰腺癌的影响的调查上也得到了上述趋势，即在很低浓度时THM的致癌性可忽略，超过一定浓度后致癌性随之增强。故作者参考King等［5］的统计数据，认为当THM 浓度在0～24μg／L时其服务水平为100%，当THM 浓度在24～70μg／L之间时服务水平呈线性递减。

基于以上分析，得到以下THM服务水平评价函数：

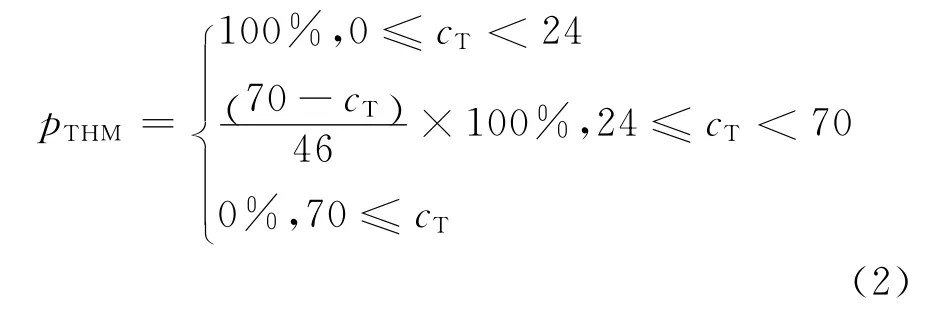
式中cT为THM 浓度，μg／L。

2 优化模型

由于经济、技术等方面因素的制约，二次加氯下供水管网水质服务水平需考虑以下3个目标：一是最大化余氯服务水平（fc），提高余氯消毒能力且不带来嗅味问题；二是最大化THM服务水平（fTHM），减小由THM带来的致癌性；三是最小化加氯费用（W），使得二次加氯经济性得到体现。其中fc和fTHM之间、fc和W之间相互矛盾，3个目标函数可组成多目标模型进行求解，多目标模型归纳如下：

式中：pcij和pTHMij分别代表监测点i在j时刻的余氯服务水平和THM服务水平；Qij为监测点i在j时刻的节点流量；M为周期内监测次数；M1为设备折旧大修理费；M2为材料及动力费；Eq为设备建造费；t为投资偿还期；Cik，in为加氯点i在时段k的加氯浓度；Qik，in代表加氯方式为FPB下加氯点i在时段k时流向节点i的所有管段流量总和；Us为每生产1kg次氯酸钠耗盐量；Es为氯化钠价格；Ue为每生产1kg次氯酸钠耗电量；Ee为电价；pq为每年扣除的折旧和大修费，以设备建造费的百分比计。

式（5）和（7）中需要计算加氯点设备费用总和，故模型中需要考虑加氯站的数量和选址。在加氯点选址模型中，根据pc的定义，当余氯浓度为0.125mg／L时，pc＝50%即仅能接受的服务水平。令余氯浓度大于等于0.125mg／L为被节点i覆盖，小于0.125mg／L为不被节点i覆盖。当余氯浓度为0.7mg／L时pc为50%即仅能接受的服务水平，以此令加氯点的加氯量为0.7mg／L。故采用基于余氯服务水平的加氯点选址模型：

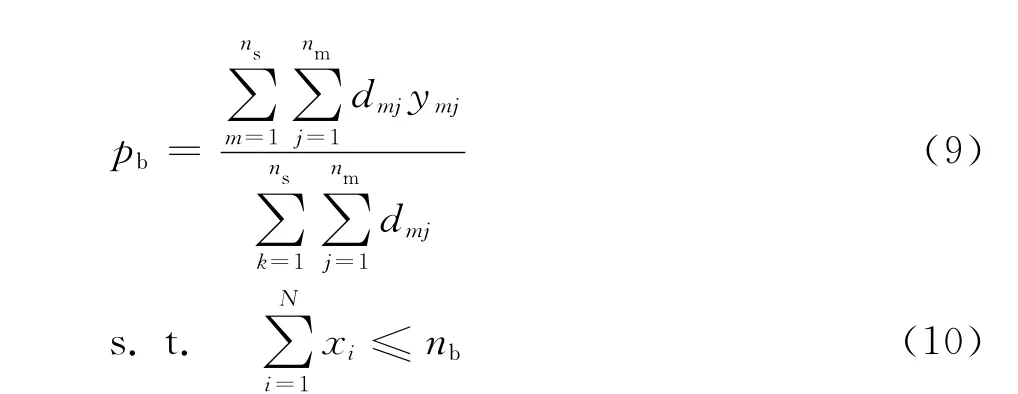
3 模型求解

3.1 THM－I／O模型推导

为提高THM浓度的计算效率，希望同余氯I／O模型一样得到THM－I／O模型，这就要求THM生成模型也具有一定形式上的线性特性。基于余氯消耗的THM线性生成模型使用方便，表达式简单，近年来在试验拟合及数值模拟方面越来越受到重视［7－9］。模型表达式如下：

式（12）只针对静止水中的THM变化情况，对于管网中任意管段内，需要考虑流动水体对THM的输送作用。设任意管段s，其两个端节点编号为i、j，水从节点i流向节点j。参考Boccelli等［6］提出的余氯传输方程，推导THM传输偏微分方程如下：

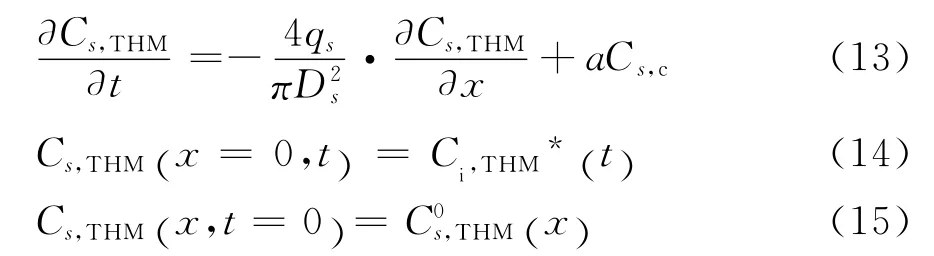
同时需考虑余氯传输偏微分方程［6］：

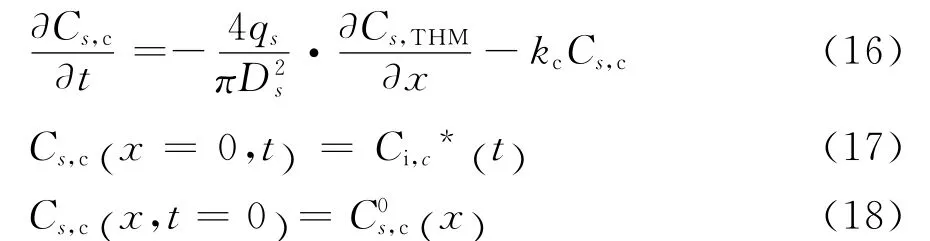
Cs，THM和Cs，c分别为THM 和余氯在管段s中的浓度，qs为管段s的流量，Ds为管段s的直径，（x）和分别为管段各处初始 THM 和余氯浓度，和分别为管段上游节点i任意时刻的的THM和余氯浓度。将式（16）代入式（13）可得：

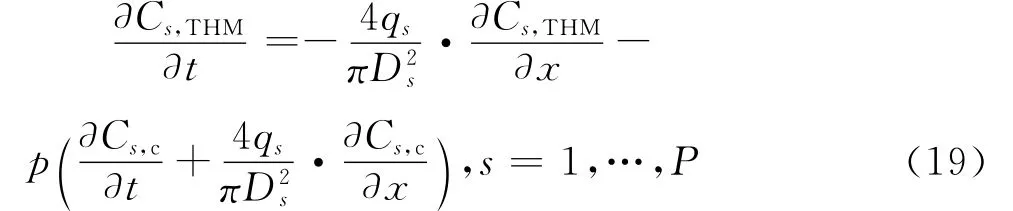
将式（19）进行对x的有限差分，可得到式（20）。

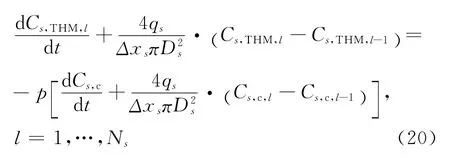
初始条件和边界条件同上，其中Δxs为有限差分点之间的距离，Ns为差分点数量.

THM和余氯在管网节点处采用均匀混合模型。考虑二次加氯点，余氯在i处的节点混合模型为［6］：

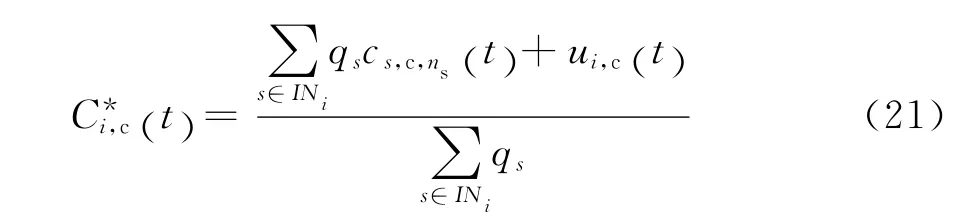
其中ui，c（t）为二次加氯点的投加量。INs为所有与节点i连接的管段集合，ns表示流入节点i的管段。推导THM在i处的节点混合模型为：

在清水池及水塔中，设余氯衰减和THM生成仍符合管段中的规律，则余氯和THM流出清水池或出入水塔的表达式均可写成式（23）、（24）。

根据以上分析可见，余氯和THM在管段、节点、清水池或水塔中的变化均符合线性规律.则对于所有管段所有差分点和首末节点处在k时段内的THM 和余氯浓度组成的浓度向量 Ck，THM、Ck，c，将（20）、（21）、（23）和（24）式矩阵化后满足式（25）。

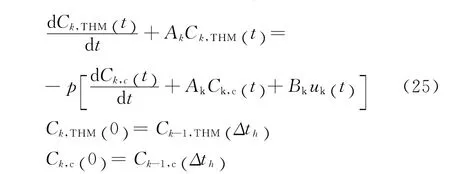
式中Ak、Bk由管道流量、管网节点分布及管网拓扑结果确定。

将式（25）拉普拉斯变换处理可得［6］：

其中：

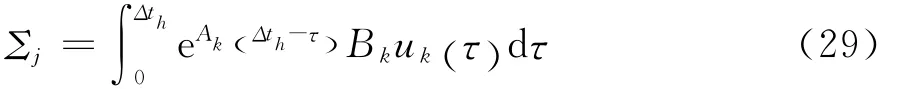
对周期内所有时段k＝0，1，…，J的式（27）采用βk进行加权后相加，可得最终表达式：

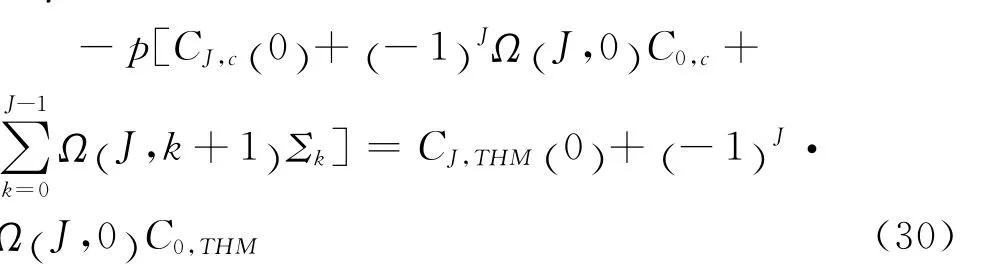
式中Ω（k，l）＝βk－1βk－2…βl，k＞l，且Ω（k，k）＝I。由于周期时间长，初始余氯和THM浓度对监测点影响很小，Ω（J，0）C0，THM及Ω（J，0）C0，c可忽略不计，又Cj，c（0）仅由加氯点线性确定［6］，故可知管网所有节点的THM浓度只由加氯点线性确定。故可得THM浓度可像余氯浓度计算一样采用I／O模型进行计算。

3.2 模型算法

对多目标模型采用多目标遗传算法（NSGA－Ⅱ）求解，具体步骤为：

第1步，根据余氯I／O模型和THM－I／O模型采用EPANET＿MSX工具包得到余氯响应矩阵和THM响应矩阵，保存于内存中。运行过程中管网水力持续时间为30d，目的是使得水质条件达到稳定。

第2步，采用多目标遗传算法（NSGA－Ⅱ）求解模型，其中种群规模取100，计算代数为500代，染色体编码采用实数编码，选择算子为联赛选择，采用精英保留策略。

4 算例分析

为分析多目标模型求解结果及考察主体水余氯衰减系数、THM比例系数、出厂水THM浓度及加氯点数量对求解结果的影响，采用如图1所示的管网进行分析。此管网为EPANET2.0自带算例Net3，共91个用户节点、2个水源及3座水塔，部分节点编号示于图中。此管网湖水源在13：00到次日4：00开启，其余时间关闭。水源条件的切换导致水力条件改变，管网中编号为203和15的节点用水量较其他节点高出10倍以上，对加氯点选址及多目标模型计算影响很大。故在采用节点用水量加权计算fc和fTHM时将此2节点用水量减小至500GPM，既减小了两者的影响，又保持了大流量的特点。单位加氯点设备费为2万元，Us为4.1kg，Es为1.6元／kg，Ue为4.4kW，Ee为0.85元／kW，Wmax为300元。

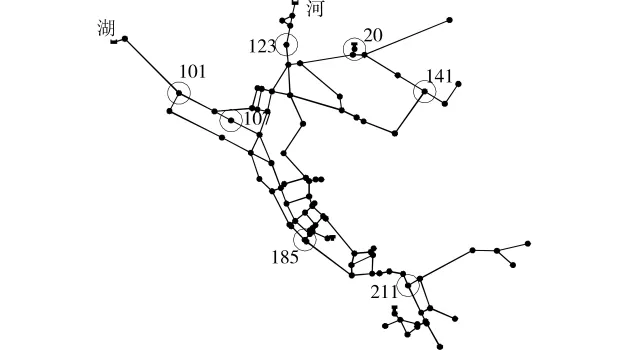
图1 Net3算例

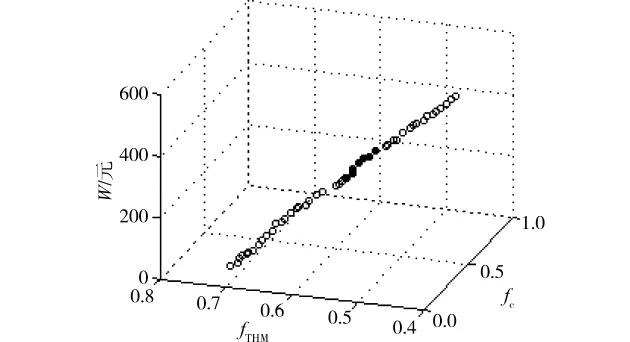
图2 设计目标的Pareto前沿面

图2显示了nb＝5，kb＝ －6d－1，kw＝－3m／d，THM0＝35μg／L，p＝35时多目标模型计算结果。其中 THM0＝35μg／L指2水源出厂水均为35μg／L。原因是在不加氯情况下当管网水质运行稳定后的THM服务水平达到稳定，故无论2水源出厂水THM0是否相同，对考察出厂水THM0对多目标模型求解结果的影响是没有区别的。由图可见计算程序能够得到Pareto前沿面，并且得到了fc从0到较优水平的范围。多目标模型的Pareto前沿面接近曲线，可见W和fTHM存在较弱的矛盾关系，原因是W中的M1代表了余氯的投加，无论管网末梢余氯浓度为多少M1仍然以加氯点的投加量计算，而fTHM是以余氯的实际消耗量计算的，即由加氯点的余氯投加浓度和管网末梢的余氯浓度两者决定的，故结果出现Pareto前沿面并非严格曲线的结果。

由于存在约束条件，Pareto前沿面分成2类点.图中空心点为不满足约束条件的结果，实心点为满足约束条件的结果。增加THM服务水平的约束条件比只考虑余氯服务水平和加氯费用进一步减少多目标求解结果选择范围，可更加接近实际情况。

为考察不同kb下Pareto前沿面变化趋势，采用nb＝5，THM0＝35μg／L，p＝35不变，kb＝－6、－4、－3d－13种情况进行比较，为更好的观察变化趋势，将计算结果的Pareto前沿面投影到fTHMfc面和Wfc面上组成如图3的投影组合面（下同），图中实心点表示fTHMfc面的投影结果，空心点表示Wfc面的投影结果（下同）。由图可见在相同fc情况下，随着kb的增加，W随之减速增加，而fTHM随着kb的增加减速减小。此结果表明，随着余氯主体水衰减系数的增加，余氯衰减加快，使得达到相同fc所需的加氯量增加，且余氯消耗加大，又由于THM增加量与余氯消耗呈线性关系，故fTHM减小。

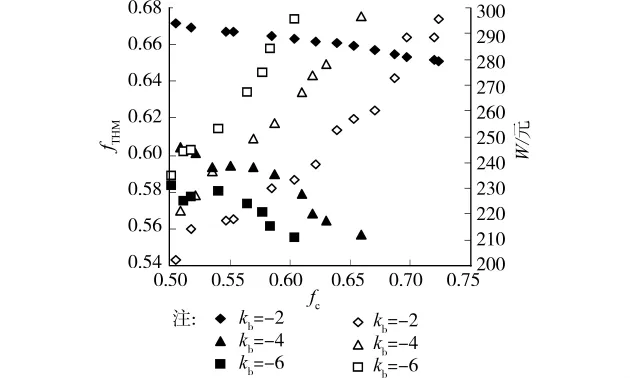
图3 不同kb下Pareto前沿面变化趋势

由于生成THM的前驱物在各季节可能发生改变，以及溴离子和氨氮对THM生成量的影响，需考虑p值的变化。为考察比例系数p对Pareto前沿面的影响，采用nb＝5，THM0＝35μg／L，kb＝－6d－1不变，p＝10、20、30的3种情况进行比较。由图4可见，随着p值的减小，相同fc情况下fTHM增大，但是W值基本不变，原因是p值改变只影响了THM的生成，对余氯衰减没有影响，余氯消耗没有变化。

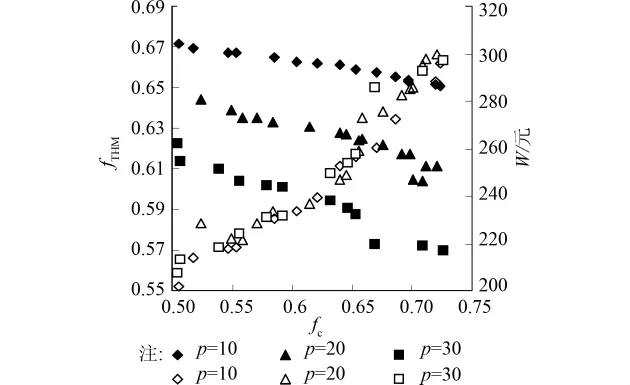
图4 不同p值下Pareto前沿面变化趋势

水厂消毒工艺需在清水池中加氯消毒，保证出厂水余氯浓度达到国家标准。在传统工艺下难免使得出厂水中含有一定浓度的THM，故出厂水THM浓度的大小直接决定了管网fTHM的最大值，即在没有加氯时的THM服务水平，可见需要考虑出厂水THM浓度对计算结果的影响。采用nb＝5，p＝30，kb＝－2d－1不变，THM0＝30、32.5、35μg／L 3种情况进行比较，得到如图5所示结果。由图可见随着THM0的增加相同fc下的fTHM减小，而对W值没有影响，原因是THM0的影响和p值一样只影响了THM浓度而不改变余氯浓度。

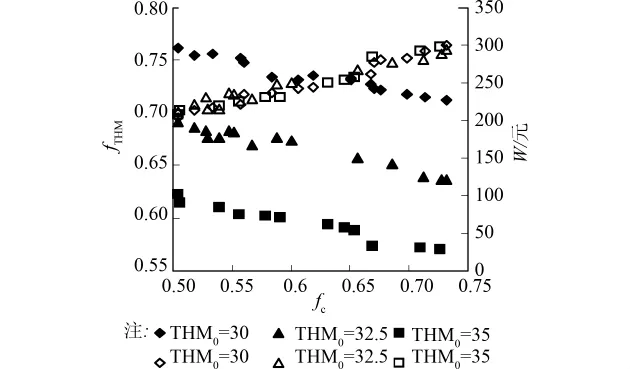
图5 不同THM0下Pareto前沿面变化趋势

为研究加氯点数量对多目标模型Pareto前沿面的影响，考察p＝30，kb＝－2d－1，THM0＝35不变，nb＝3、4、5、6、7共5种情况下Pareto前沿面的变化情况，各加氯点方案由式（9）、（10）确定，7个加氯点位置示于图1中，加氯点编号示于表1中，由图可见加氯点选址模型能够得到水源节点及下游节点，与二次加氯要求的加氯点均匀分布要求吻合。

表1 不同加氯点数量下加氯点方案

图6为各加氯点方案下Pareto前沿面在fcW面上的投影，实心点表示符合约束条件的加氯方案，空心点表示不符合约束条件的加氯方案。由图可见，当fc为零，即不加氯时增加一个加氯站W相应的增加一个加氯站的建设费用，各方案的W差值最大，随着fc的增加，各方案的W差值逐步缩小。原因是加氯站的增加能够使得余氯在管网内的分布更加均匀，并且减少余氯的投加。可见计算结果符合以往文献得出的规律。当nb增加时，fc最大值相应增加，可见在不考虑约束条件的情况下增加nb可提高最优fc的值，但是由于约束条件的影响，要达到最优fc必然需要更多的投入，并且THM的服务水平会相应的降低。由图可见实心点在较小范围内存在，并且随着nb的增加W为先减后增，但是各方案的差别不大。

图7显示了各加氯点方案下Pareto前沿面在fc－fTHM面上的投影。由图可见在不考虑约束条件下增加nb可提高在较大fc情况下的fTHM值。但是由于约束条件的影响，fTHM随着nb的增加变化有限，并且在较大nb情况下fTHM有所减小，原因是THM的生成是随着余氯的消耗而线性增加，故余氯越均匀在传输过程中余氯消耗的越多，相应的THM生成就增加。综上可见增加nb对Pareto前沿面的影响较小，较多的nb值反而会加大建设投入。

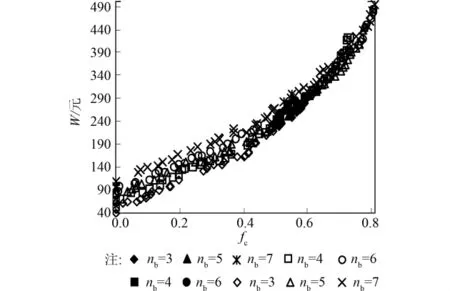
图6 不同加氯点数量下Pareto前沿面变化趋势

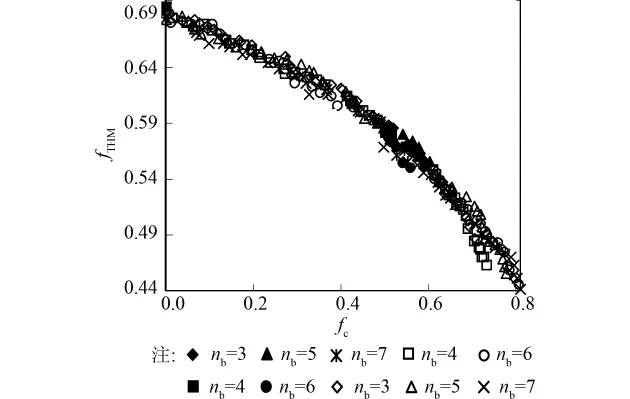
图7 不同THM0下Pareto前沿面变化趋势

5 结 论

根据病理学的调查统计结果，提出了线性化的THM服务水平评价函数，与余氯服务水平评价函数一起组成了管网基本水质的服务水平评价方法。验证了THM－I／O模型，大大提高了算法的效率。考虑THM服务水平可减少多目标优化结果可选方案的数量，对主体水余氯衰减系数、基于余氯消耗的THM生成比例系数、出厂水THM浓度、加氯点数量4个影响因素对Pareto前沿面计算结果比较后发现，主体水余氯衰减系数的减小是提高余氯和THM服务水平及减小加氯费用最经济有效的方法，故在建设二次加氯站前建议在水厂处理工艺中尽量提高水质，降低余氯衰减系数。

［1］张燕，张念卿.基于部分覆盖理论的供水管网二次加氯点选址［J］.浙江大学学报：工学版，2011，45（4）：695－707.ZHANG Yan，ZHANG Nianqing.Optimization of locations of booster chlorination stations in water distribution system based on theory of partial coverage［J］.Journal of Zhejiang University： Engineering Science，2011，45（4）：695－707.

［2］Tamminen S，Ramos H，Covas D.Water supply system performance for different pipe materials part I：water quality analysis ［J］.Water Resources Management，2008，22（11）：1579－1607.

［3］Chowdhury S，Champagne P，Mclellan P J.Models for predicting disinfection byproducts（DBP）formation in drinking waters：a chronological review ［J］.Science of the Total Environment，2009，407（14）：4189－4206.

［4］Carrico B，Singer C.Impact of booster chlorination on chlorine decay and THM production：simulated analysis［J］.ASCE Journal of Environmental Engineering，2009，135（10）：928－935.

［5］King W D，Marrett L D.Case－control study of bladder cancer and chlorination by－products in treated water（Ontario，Canada）［J］.Cancer Causes and Control，1996，7（6）：596－604.

［6］Do M T，Birkett N J，Johnson K C，et al.Chlorination disinfection by－products and pancreatic cancer risk［J］.Environmental Health Perspectives，2005，113（4）：418－424.

［7］Brown D，West J R，Courtis B J，et al.Modeling THMs in water treatment and distribution systems ［J］.Proceeding of the Institution of Civil Engineers－Water Management，2010，163（4）：165－174.

［8］Courtis B J，West J R，Bridgeman J.Chlorine demandbased predictive modeling of THM formation in water distribution networks［J］.Urban Water Journal，2009，6（6）：407－415.

［9］Liu W，Qi S.Modeling and verifying chlorine decay and chloroacetic acid formation in drinking water chlorination［J］.Frontiers of Envronmental Science ＆Engineering in China，2010，4（1）：65－72.

［10］Boccelli D L，Tryby M E，Uber J G，et al.Optimal scheduling of booster disinfection in water distribution systems ［J］.ASCE Journal of Water Resources Planning and Management，1998，124（2）：99－111.

［11］黄鑫，高乃云，丁国际，等.溴酸根在紫外和氯消毒联用工艺中的形成［J］.土木建筑与环境工程，2010，32（6）：132－136.HUANG Xin，GAO Naiyun，DING Guoji，et al.Formation of Bromate in UV／Cl2，UV／NH2Cl and UV／ClO2combining processes ［J］.Journal of Civil，Architectural and Environmental Engineering，2010，32（6）：132－136.

［12］赵纯，邓慧萍，商冉.改进紫外消毒工艺中去除水中土霉素［J］.土木建筑与环境工程，2009，31（2）：152－156.ZHAO Chun，DENG Huiping，SHANG Ran.Removal of oxytetracycline in water by improved UV disinfection process ［J］.Journal of Civil， Architectural and Environmental Engineering，2009，31（2）：152－156.

［13］张土乔，王鸿翔，郭帅.给水管网水质模型管壁余氯衰减系数校正［J］.浙江大学学报：工学版，2008，42（11）：1977－1982.ZHANG Tuqiao，WANG Hongxiang，GUO Shuai.Chlorine wall decay coefficients calibration of water distribution quality model ［J］.Journal of Zhejiang University：Engineering Science，2008，42（11）：1977－1982.

［14］李寻，张土乔，翁风永，等.基于节点水龄的供水管网水质研究［J］.中国给水排水，2009，25（19）：103－105.LI Xun，ZHANG Tuqiao，WEN Fengyong，et al.Study on water quality in water distribution system based on water age of nodes［J］.China Water and Wastewater，2009，25（19）：103－105.

［15］Visalakshi S，Baskar S.Multiobjective decentralized congestion management using modified NSGA－Ⅱ ［J］.Arabian Journal for Science and Engineering，2011，36（5）：827－840.

［16］Shen H，Mcbean E.Pareto optimality for sensor placements in a water distribution system ［J］.Journal of Water Resources Planning and Management，2011，137（3）：243－248.