水平管道内冰浆流动阻力特性预测模型及比较

梁运涛，王树刚，张腾飞，王继红

（1.煤炭科学研究总院沈阳研究院 煤炭安全技术国家重点实验室，沈阳110016；2.大连理工大学 土木学院，大连116024）

区域供冷在城市用电结构优化中扮演重要角色［1］。冰浆流体作为蓄冷介质，因具有良好的热物性、传输性及相变特性正日益受到人们广泛关注。作为冰浆介质工程推广的基础性研究，冰浆流体阻力特性成为当前各国学者的研究热点。目前所采用的研究方法多以实验测试为基础，结合描述冰浆流体的Bingham、Herschel－Bulkley、Powder Law 和Casson等非牛顿流变特性［2－5］，建立冰浆流体管道压降预测模型。此类模型虽然能够在一定范围内较为便捷地预测出冰浆流体阻力特性，但适用条件苛刻，难以同时兼顾输送管径、管速、冰粒子的浓度、粒径、载流体的种类及添加剂的浓度等多因素对阻力特性的影响。近年来，固液两相流计算流体力学（CFD）模拟技术为研究冰浆流体阻力特性带来了新的契机。笔者以冰粒子与载流体所构成的固液混合物为研究对象，采用无相变过程的两相流混合模型，运用CFD模拟为工具，对不同工况下浆体所表现出的牛顿与非牛顿流变特性给予分段考虑，将CFD模拟结果与既有文献实验数据及其它模型预测结果进行对比分析。

1 数学模型

基于无相变过程的两相流混合模型［6－9］，描述其流动特性的数学模型可表示如下。

1.1 连续性方程

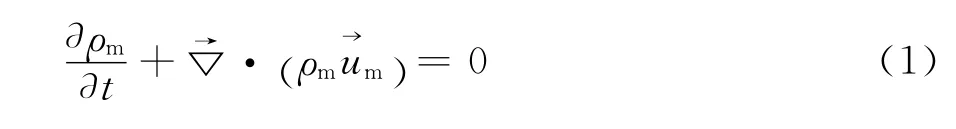
式中：ρm为混合相流体的密度，kg·m－3；um为混合相流体的速度，m·s－1；▽为拉普拉斯算子。

1.2 动量方程

式中：i＝1和2分别为液体相和冰粒子相；p为静压力，Pa；τm为剪切应力，Pa；αL和αS分别为液体相和冰粒子相的体积浓度，%；uDi为拖曳速度，m·s－1。

1.3 冰粒子相浓度方程

基于无相变过程的冰粒子相浓度方程，如式（3）所示。

1.4 湍流方程

以求解雷诺平均的纳维尔 斯托克斯方程（RANS）为基础，描述混合相流体湍动的k－ε方程，如式（4）和（5）所示。

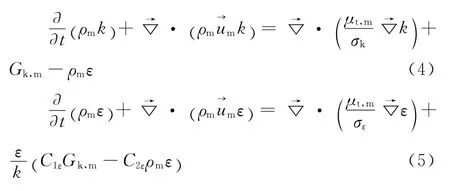
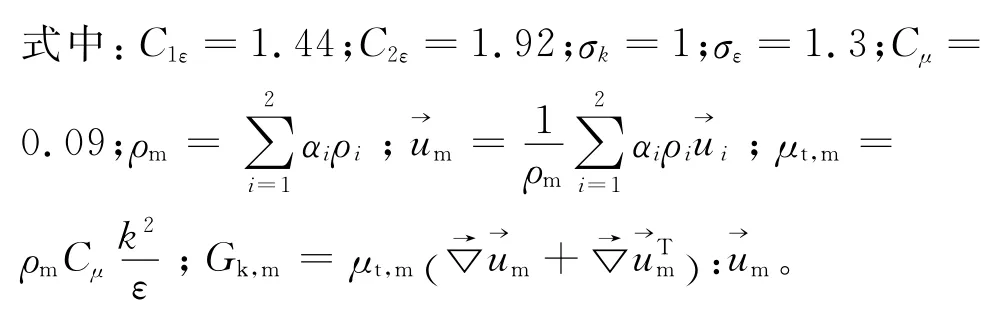
1.5 封闭条件

1.5.1 拖曳速度模型 多相流中，拖曳速度uDi表示i相与混合相间速度差。据此定义可得冰粒子相与液体相的拖曳速度，如式（6）和（7）所示［6］。

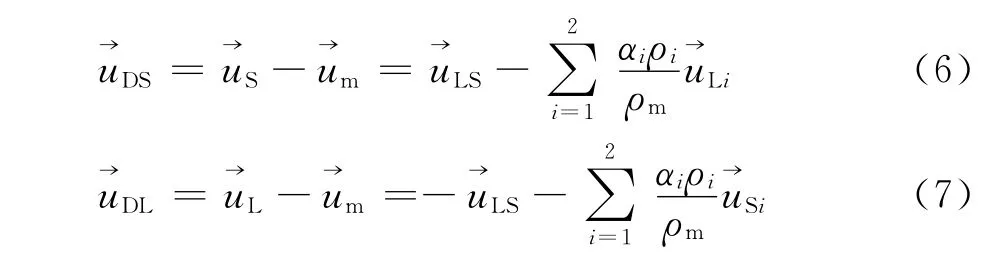
式中：uLS为液固两相间的滑移速度，m·s－1，其具体计算关系如式（8）和（9）所示［6］。

式中：dS为冰粒子直径，m；ReS为冰粒子雷诺数；μt，m为湍流粘度，kg·m－1·s－1；σD为普朗特扩散系数；fdrag为拖曳系数。

1.5.2 粘度模型 水平管道内冰浆流体的输送过程中，当浆体输送速度较高时，冰粒子沿管道截面近似呈均匀分布，此时Thomas方程［10］可很好地表示混合相流体的粘度特性，如式（10）所示。

式中：μm为混合相流体粘度，kg·m－1·s－1；μL为液体相粘度，kg·m－1·s－1。

随着浆体速度降低，冰粒子沿管道截面梯级分布，混合相流体非牛顿特性逐渐显现。本研究发现，若系统在低速运行时致使管道顶部冰粒子的浓度αS≥30%，此时Bingham流变模型［2］可以很好地描述出低速工况下冰浆流体的流变特性，如式（11）所示。

式中：μp为混合相流体塑性粘度，kg·m－1·s－1；τp为混合相流体屈服应力，Pa；为混合相流体速度变形率，s－1。其中，μp与τp取值见文献［11］。

采用CFD方法求解上述微分方程组，首先沿着CFD网格单元对各微分方程实施积分，然后基于散度定理离散得到相应离散方程，最后应用SIMPLE算法耦合连续性与动量方程。方程求解的边界条件类型在管道入口为质量流率入口，出口为压力出口。湍流流动时壁面处应用标准壁面函数。流动计算区域采用六面体网格单元，平均尺寸为1.7mm。通过对所获得的数值计算结果进行网格独立性检验，网格数量符合独立性要求。数值计算精度满足前后两次迭代值相对误差小于10－6。

2 算例验证与对比分析

2.1 算例概况

以文献［12］所报道的实验结果为参考，利用前文所介绍的两相流CFD模拟方法研究水平管道内冰浆流体等温流动过程。其中浆体输送管径D＝0.016m，管长L＝6m，输送平均速度um＝0.22～2.02m·s－1，液体相为质量浓度CA＝10.6%的乙醇溶液。各相基本物理参数如表1所示。

表1 流体的基本物理参数

2.2 数值结果分析

图1给出了不同浓度下水平管道内冰浆流体管道压降与平均输送速度间变化关系。总体上浆体的管道压降与平均输送速度间呈单调递增关系，但在低速流动区域内（本例中，输送速度小于0.78m·s－1），压降随输送速度的递变速率略有降低。由图1（a）可知，当采用Thomas粘度方程时，CFD模拟结果与实验值整体上体现出较好的一致性，但随着浆体速度的降低，CFD预测值明显低于实验测试结果，在某些低速工况点处最大偏差可达48.9%。这是因为随着浆体速度降低，管道顶部冰粒子浓度升高，此时冰浆流体逐渐表现出非牛顿流体特性。在所验证的4组工况中，当浆体输送速度低于0.78m·s－1、管道顶部冰粒子浓度高于30%时，冰粒子沿管道截面分布不均匀性加剧，粒子间相互作用增强，此时Thomas粘度方程的高阶项不足以反映冰粒子间相互作用，以及由此造成的混合相流体粘度特性的变化。但是，借助于Bingham流变模型，则可较为理想地刻画出低速工况下水平管道内冰浆流体的非牛顿特性。基于Bingham流变特性并采用两相流无滑移混合模型，对图1（a）中虚线内工况点进行修正处理。由图1（b）可知，在修正后低速工况点处，CFD模拟获得了与实验测试非常一致的结果，最大偏差不足15%。

图1 水平管道内不同冰浆浓度下冰浆流体的管道压降

2.3 预测模型对比

冰浆流体管道压降受多因素制约，而现行的基于宏观实验现象所建立起的阻力特性预测模型往往难以很好地平衡模型的精度与通用性间关系。这是因为此类模型多是借助于冰浆流体非牛顿流变特性，再结合单相流体的Darcy阻力关系建立的。在建模过程中，由于实验条件所限，难以综合考虑多类影响因素。以图1中所描述的各工况点为例，分别选取文献［13］、［14］及［15］所建立的3类具有代表性的管道压降预测模型进行计算，其详细的数学描述如表2所示。

图2给出了各类预测模型的预测结果与实验对比。由图2中（a）、（b）及（c）不难发现，文献［13］所介绍的压降预测模型虽能较好地预测出大部分工况点的压降值，但在个别工况点处模型预测精度并不稳定，预测效果的阶跃性及随机性较大。而文献［14］和［15］所建立的预测模型仅在高速、低浓度工况下体现出较好的预测效果，当浆体浓度升高、输送速度降低时，模型预测值与实验值间产生较大偏差，从而大大削弱了预测模型的实用价值。图2（d）为所采用的CFD模型预测结果，由对比可知，模拟值与实验值间的相对误差可控制在±15%内，模拟结 果与实验测试结果吻合良好。

表2 冰浆流体管道压降预测模型数学描述

图2 水平管道内冰浆流体管道压降预测模型的预测值与实验值对比

3 结 论

采用两相流混合模型，对不同工况下浆体所呈现的牛顿与非牛顿流变特性给予分段考虑，通过CFD模拟方法研究了水平管道内冰浆流体的等温流动，结论如下。

1）在水平管道内冰浆流体输送过程中，当浆体速度较高时，冰粒子沿管道截面近似呈均匀分布，此时Thomas方程可很好地描述混合相流体的粘度特性。随着浆体速度降低，管道顶部冰粒子浓度升高，冰浆流体逐渐表现出非牛顿流体特性，此时利用Bingham流体模型来描述低速工况下混合相流体的流变特性所获得的效果较为理想。

2）同基于冰浆流体非牛顿流变特性管道压降预测模型相比，笔者所采用的数值计算模型因全面考虑到浆体输送管径、管速、冰粒子的浓度、粒径、载流体的种类及添加剂的浓度等多因素影响，模型的精度与通用性可得到较好平衡。在所验证的4组工况中，采用的数值模型的预测值与实验值之间的相对误差均控制在±15%以内。

［1］魏琪.等热流圆管内冰浆流体传热特性的解析研究［J］.苏州大学学报，2006，26（3）：1－3.WEI Qi.Analytical study on heat transfer of ice slurry in a circular tube with constant heat flux［J］.Journal of Soochow University：Engineering Science，2006，26（3）：1－3.

［2］Grozdek M， Khodabandeh R， Lundqvist P.Experimental investigation of ice slurry flow pressure drop in horizontal tubes［J］.Experimental Thermal and Fluid Science，2009，33（2）：357－370.

［3］Illan F，Viedma A.Experimental study on pressure drop and heat transfer in pipelines for brine based ice slurry Part II：dimensional analysis and rheological model ［J］.International Journal of Refrigeration，2009，32（5）：1024－1031.

［4］Ayel V，Lottin O，Peerhossaini H.Rheology，flow behaviour and heat transfer of ice slurries：a review of the state of the art ［J］.International Journal of Refrigeration，2003，26（1）：95－107.

［5］Kitanovski A，Vuarnoz D，Caesar D A，et al.The fluid dynamics of ice slurry ［J］.International Journal of Refrigeration，2005，28（1）：37－50.

［6］Ling J，Skudarnov P V，Lin C X，et al.Numerical investigations of liquid－solid slurry flows in a fully developed turbulent flow region ［J］.International Journal of Heat and Fluid Flow，2003，24（3）：389－398.

［7］Lin C X，Ebadian M A.A numerical study of developing slurry flow in the entrance region of a horizontal pipe［J］.Computers ＆Fluids，2008，37（8）：965－974.

［8］Skudarnov P V，Lin C X，Ebadian M A.Doublespecies slurry flow in a horizontal pipeline［J］.Journal of Fluids Engineering，2004，126（1）：125－132.

［9］张宏兵，陈露露，谢荣华.水平圆管固液两相稳态流动流动特性数值模拟［J］.化工学报，2009，60（5）：1162－1168.ZHANG Hongbing，CHEN Lulu，XIE Ronghua.Numerical simulation of solid－liquid two－phase steady flow in horizontal pipe ［J］.Journal of Chemical Industry and Engineering，2009，60（5）：1162－1168.

［10］Thomas D G.Transport characteristics of suspension［J］.Journal of Colloid Science，1965，20（3）：267－277.

［11］Beata N Z，Zelasko J.Generalized non－Newtonian flow of ice－slurry［J］.Chemical Engineering and Processing，2007，46（10）：895－904.

［12］Beata N Z，Wojciech Z.Momentum transfer of ice slurry flows in tubes，experimental investigations［J］.International Journal of Refrigeration，2006，29（3）：418－428.

［13］Tomita Y.On the fundamental of non－Newtonian flow［J］.Bulletin of the Japanese Society of Mechanical Engineers，1959，2（7）：469－474.

［14］Kauffeld M，Kawaji M，Egolf P W.Handbook on ice slurries－fundamentals and engineering ［M］.France：International Institute of Refrigeration，2005.

［15］刘永红.冰浆流动特性和传热性能的研究［D］.上海：同济大学，1997.